
百萬年前,人類與動物沒有太大差別,撿撿石頭、樹枝、果子。但跟其他動物相比,人類太過於弱小,為了提升在自然界的存活率,人類開始製作石器,進入了石器時代。隨著時間演進,人們開始學會以火製作陶器,甚至煉製金屬。到了十九世紀,更有了煤礦與合金,工業革命因此產生。石油與半導體可說是二十世紀的代表,我們的生活都與這兩樣東西息息相關。二十一世紀雖還沒結束,但我們已將高溫超導體用於醫療核磁共振 (Nuclear Magnetic Resonance) ,巨磁阻 (magnetoresistance) 材料則是大容量硬碟的基礎。至此,我們可發現,人類生活方式的演進與材料發展緊密相連,材料的歷史可說是人類的歷史。
 能帶理論
能帶理論
凝態物理 (condensed matter physics) 是物理領域中專門研究物質 ( 材料 ) 性質與相變 (phase transition) 的一個子領域,而能帶理論 (Energy band theory) 更是其中最具代表性的理論。如圖 1 (a) 所示,對於一顆原子,量子力學給出不連續的能階分佈,如果將大量的原子放在一起且形成晶格 (lattice) 排列,此時系統的能量分佈將不再是一段一段的獨立能階而是呈現連續的帶狀分佈,稱之為能帶結構 (Energy band structure) ( 圖 1 (b)) 。能帶就像道路一般,電子佔據能帶也可以在能帶上移動。電子由最低的能帶一層一層向上填,填滿的部分稱為價帶 (valence band ,VB) ,未填的部分為導帶 (conduction band ,CB) ,所填至的最高能階則稱為費米能級 (Fermi level) 。雖然能帶理論的物理圖像非常簡單,但已提供足夠的能力讓我們去辨別材料的物質相。例如價帶與導帶中間被一能隙 (energy gap) 所分開,電子無法從價帶移動到導帶,此時電子無法輕易在材料中傳輸形成電流,稱為絕緣體 ( 圖 1 (c)) 。反之如果費米能級穿過導帶,電子能輕易在能帶上移動,材料將會呈現出金屬性質 ( 圖 1 (d)) 。在能帶理論的架構下,藉由量子力學方法研究材料中電子與電子或電子與晶格的交互作用,使我們得以深入了解材料中的各種物理性質。
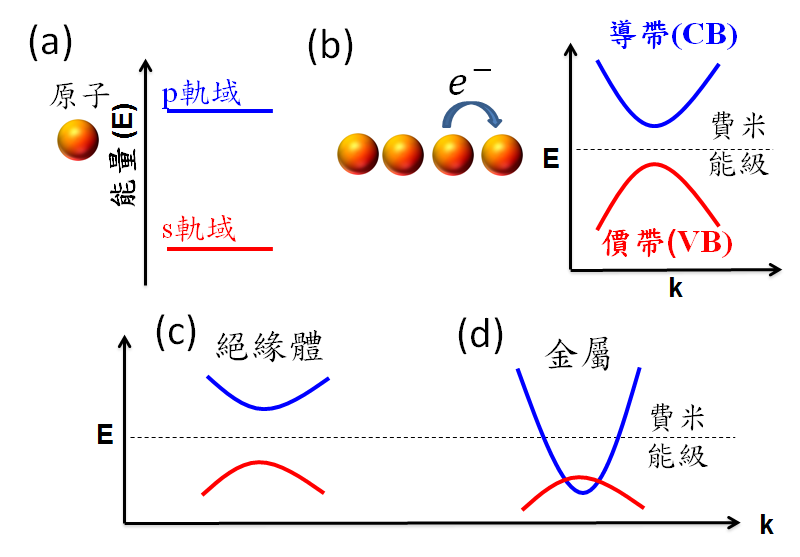
圖
1.
(a)
原子能階。
(b)
能帶結構。(c) 絕緣體能帶結構。(d) 金屬能帶結構。
 材料中的拓樸
材料中的拓樸
接著我們來看看什麼是材料中的拓樸。拓樸乍聽之下比較像抽象的數學,和實際的材料似乎八杆子打不著關係。簡單來說,在拓樸中不需要去關心系統的幾何形狀,只需辨別系統上
「洞」
的數目。數學上習慣討論實空間
(real space)
的
拓樸,我們可以用
Gauss-Bonnet Theorem:
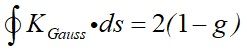
來辨別系統的拓樸。這裡我們不討論數學上的細節,根據
GB Theorem
,相同的g代表系統具有相同的拓樸,即使幾何形狀完全不同。
如果一個
系統
能連續變化到另一個
系統
,那這兩個
系統
的拓樸會完全相同
(
例如你去壓或拉一顆皮球,只會改變它的形狀,不會使它產生
「
洞」,因此連續變化不會改變g的值
)
。
而不同的g則代表不同的拓樸。一個最有名的例子,咖啡杯的拓樸和甜甜圈是相同的,但與菠蘿麵包不同。除非你把麵包咬出一個洞,不然絕對無法把麵包扭成甜甜圈
(
圖
2)
。
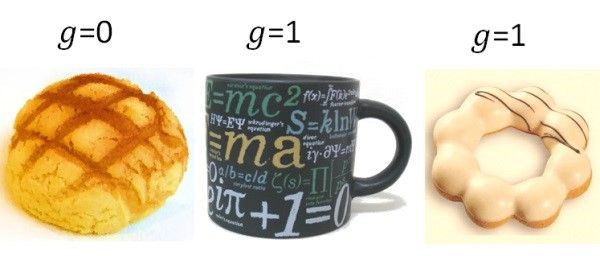
圖 2. 實空間的拓樸。菠蘿麵包 (98-2nd 麵包義賣照片 ) 。甜甜圈 (Biscuit Q 堤甜甜圈 )
物理上我們熟悉的是能帶理論,因此凝態物理的拓樸則是動量空間 (momentum space) 中 的拓樸。如圖 3 所示,能帶 -1 與能帶 -2 的形狀 ( 註 1) 非常相似,但它們的拓樸卻不相同,能帶 -2 與能帶 -3 在形狀上完全不同,但它們卻帶有完全相同的拓樸數。為了更深入了解能帶的特性,我們將原子軌域投影到能帶上 ( 註 2) 。假設一個 NaCl 系統,藍點代表 A 原子的貢獻 ( 例如 Na) ,紅點則是 B 原子的貢獻 ( 例如 Cl) 。在能帶 -1 中,導帶全由 A 原子所構成而 B 原子則佔據了價帶。這符合我們的預期,因為在 NaCl 中, Na 的電子會轉移到 Cl 上, Cl 因獲得額外的電子而降低能量。在這裡我們稱這種現象為化學鍵順序 (Chemical bond order) 。在能帶 -1 中,因為導帶或價帶全由同一種原子所構成,因此在能帶上的波函數不會有奇異點 (singular point) , 是一個平滑函數。在能帶 -2 中,價帶幾乎由 B 原子佔據,但我們可以發現,其中有一個點卻表現出A原子的特徵 ( 藍點 ) 。因為B原子無法連續變化成A原子,因此這現象就好比在 價帶上打了一個洞。 同樣的,在導帶中也可以看到類似的情況,原先由A 原子所構成的導帶卻 有一個點表現出B原子的特徵。因為能帶上具有洞的緣故,波函數也會表現出相應的特性,必定具有奇異點。由於能帶-1與能帶-2的波函數具有不同的數目的 「 洞」,因此這兩個能帶對應不同的拓樸。更仔細觀察這兩個能帶,我們可以發現從能帶- 1 變化到能帶- 2 的過程中 , A 原子由 導帶移到價帶, B 原子由 價帶移到導帶,導帶與價帶交換了它們的原子軌域 ( 圖 3 的虛線箭頭 ) 。這現象我們稱為能帶反轉 (energy band inversion) [1,2]。能帶反轉行為使得動量空間中的某些位置違反了先前提過的 化學鍵順序,能帶的波函數因此產生了額外的 「 洞」,進而引發拓樸相變。事實上,所有的拓樸相變必定會發生能帶反轉現象 ( 註 3) 。比較能帶- 2 與能帶-3,雖然它們的能帶幾何完全不同,但因能帶具有相同數目的「洞」,因此在拓樸觀點上兩者是完全相同的。
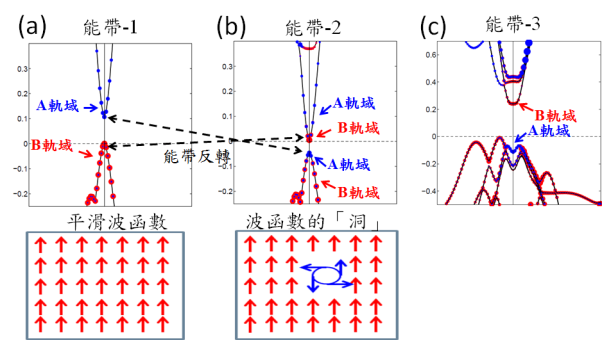
圖3. (a) 能帶 -1 。(b) 能帶 -2 。(c) 能帶 -3 。下方紅色與藍色箭頭是貝里曲率向量。
與
GB Theorem
類似,
我們可以用一條數學式來嚴格區分能帶的拓樸,專業術語為
「
拓樸不變量
」(topological invariant number)
 [3]
:
[3]
:
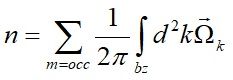
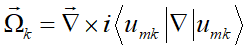
其中
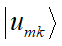 是系統的波函數,Ω
k
是貝里曲率
(Berry curvature)
。當能帶反轉發生後,波函數的奇異點能提供非零的貝里曲率,進而產生整數的
n
。一般絕緣體或半導體的
n
=0,而整數的
是系統的波函數,Ω
k
是貝里曲率
(Berry curvature)
。當能帶反轉發生後,波函數的奇異點能提供非零的貝里曲率,進而產生整數的
n
。一般絕緣體或半導體的
n
=0,而整數的
 則是拓樸絕緣體 (topological insulator) [4]。
則是拓樸絕緣體 (topological insulator) [4]。
註 1 : 相對於「拓樸 」, 能帶的斜率,曲率與能隙的大小稱為能帶的「幾何」 。
註
2
:
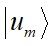 是系統的波函數。
是系統的波函數。
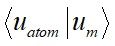 值越大代表此原子在能帶上的貢獻越大。例如能帶
-1
的導帶,
值越大代表此原子在能帶上的貢獻越大。例如能帶
-1
的導帶,
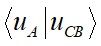 =有限
值
=有限
值
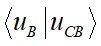 ~0。反之能帶
-1
的價帶
~0。反之能帶
-1
的價帶
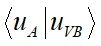 ~0,
~0,
 =有限值。
=有限值。
註 3: 能帶-1到能帶-2的能帶反轉過程為:能帶-1的能隙變小,導帶與價帶接觸並交換波函數完成反轉,之後重新打開能隙變成能帶-2。這裡所描述的理論都是單電子架構 (single particle frame),在多體 (many-body)系統下不適用。
 拓樸與實驗測量
拓樸與實驗測量
拓樸相變與傳統藍道 (Landau) 相變有著根本上的差異。藍道相變理論以「對稱性」來對物質態進行分類,當對稱性發生變化同時即反映了物質的相變。專有名詞是「對稱性破缺」(symmetry breaking)。實驗的可觀測量為物理量的期望值,因此實驗以測量系統的「有序參數」(order parameter) 來決定相變。例如當液體變成固體破壞了連續對稱性,有序參數為電荷密度,或是當鐵產生磁性時則破壞了旋轉對稱性,對應到的有序參數是磁化強度。相對於傳統相變,材料中的拓樸相變起因於能帶反轉所引發非零的貝里曲率,是在沒有破壞系統對稱性的前提下改變了物質的特性,因此傳統的藍道理論無法用於描述拓樸相變。實驗上則可藉由化學元素參雜、調控外場或外加壓力等方法來改變系統的能帶結構,使其發生能帶反轉引發拓樸相變。值得注意的是,有序參數為實驗可測量值,但拓樸不變量n 是數學量,不是可量測的期望值,因此可以預期拓樸相變的實驗可觀測量會與傳統相變完全不同。
拓樸材料最重要的物理性質存在於材料的表面或介面上,拓樸特性保證其材料的表面必定存在連接價帶與導帶的可導電表面態 (surface state,SS)(圖4) (註4) [5,6]。此表面態與一般半導體材料的表面態不同。半導體的表面態可藉由調控外場或表面原子吸附等方法將表面態移出能隙,但拓樸材料的表面態是由其整體拓樸特性所產生,不會受表面的微擾所影響,因此非常牢固 (robust)。更重要的是,這個可導電的表面態是實驗在檢測拓樸相變時唯一的可測量量。在傳統材料中絕緣體和金屬是互為水火的存在,完全不同的兩個物質相,但拓樸材料卻能同時具有材料內的絕緣性與表面金屬性。這個特殊的物質相這背後不但含有豐富的物理,更被期望可應用於製作次世代電子元件。

