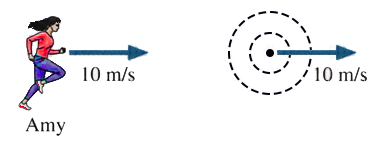
歐依～歐依～救護車就在附近，我的車需要讓路嗎？多虧「杜卜勒效應」，我們可透過警笛音調的高低，快速判斷救護車正在接近或遠離我們。但是，「杜卜勒效應」所包含的概念，可能不僅透過經驗就能掌握。透過以下10題，讓我們一探究竟。

---

小試身手

第 1~3 題：火車正在靠近一座山坡，並發出汽笛聲 (如圖 1)，若汽笛原來靜止時發出的聲音波長、頻率、波速，分別為 $\lambda_0$、$f_0$、$v_0$。山上所觀察到的聲波，為 $\lambda_1$、$f_1$、$v_1$。另外，汽笛聲撞到山壁再傳回火車的回音為 $\lambda_2$、$f_2$、$v_2$。

圖1: 火車靠近山坡

---

1. 試比較 $\lambda_0$ 與 $\lambda_1$ 兩種波長的大小關係
(A) $\lambda_0 > \lambda_1$ (B) $\lambda_0 < \lambda_1$ (C) $\lambda_0 = \lambda_1$

2. 承上題，試比較 $\lambda_1$ 與 $\lambda_2$ 之大小關係
(A) $\lambda_1 > \lambda_2$  (B) $\lambda_1 < \lambda_2$  (C) $\lambda_1 = \lambda_2$

3. 承上題，試比較 $f_1$ 與 $f_2$ 之大小關係
(A) $f_1 > f_2$  (B) $f_1 < f_2$  (C) $f_1 = f_2$

4. 承上題，若火車維持等速 $v = 30$ 公尺/秒前進，且當時音速為 $340$ 公尺/秒，則火車上的人聽到回聲的音速為多少 (公尺/秒)？
(A) 280 (B) 310 (C) 340 (D) 370 (E) 400

5. 當聲源逐漸靠近靜止之聽者時，聽者所聽得聲波之
(A)音速變快，波長變短  (B)音速不變，波長變短
(C)音速變快，波長不變  (D)音速不變，波長不變

6. 當觀察者逐漸向靜止波源靠近時，則觀察到的波速與波長，將會如何？　 (A)波速增加、波速減小  (B)波速增加、波長不變
(C)波速不變、波長減小  (D)音速不變，波長不變

7. 某人靜坐在靜止聲源之東邊，若風從西邊往東吹 (如圖2)，則此人所測得之聲波，會如何變化？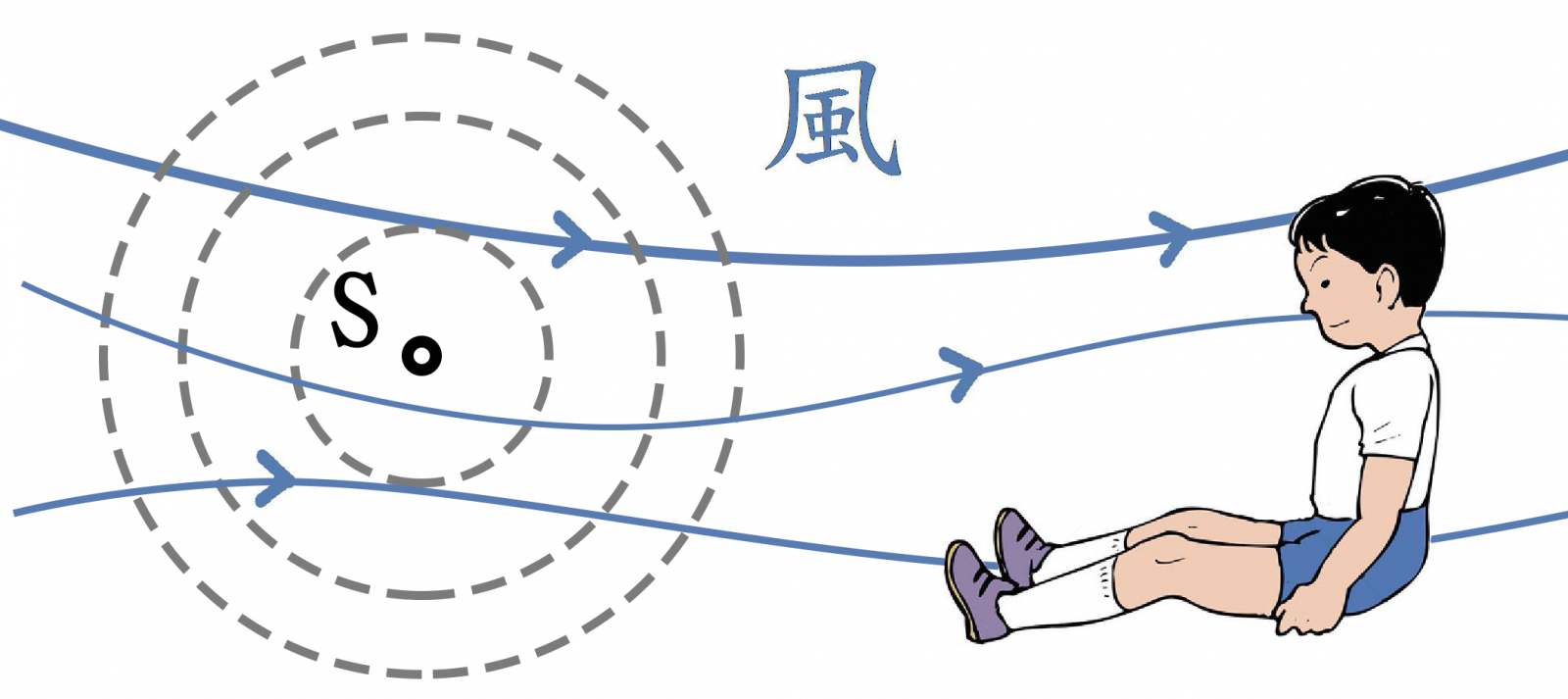

(A)音速變快，波長變長，頻率不變 (B)音速不變，波長變長，頻率變大
(C)音速變快，波長不變，頻率變大 (D)音速不變，波長變短，頻率變大
(E)音速不變，波長不變，頻率不變