人們正在尋找能將人工植入物產生的訊號傳遞到體內神經元的理想電極。生物中的碎形（Fractal），或許能帶來解答。
在我童年時期的科幻世界裡，受損的身體部位會被人工植入物取代，以恢復甚至增強功能。我百看不厭地欣賞1970年代電視節目，如《無敵金剛》（The Six Million Dollar Man）和《玄機妙算》（The Bionic Woman）的主角們如何利用他們超凡的人工眼睛和耳朵智取惡棍。
五十年過去了，這些科幻想像正在轉變為科學事實。電子裝置已經被植入眼睛，用於恢復視網膜退化性疾病患者的視力。這類疾病在50歲以上的人中，每10人就有1人罹患，且沒有常規治療方法。超過160,000例腦部植入手術，治療像是帕金森氏症（Parkinson’s Disease）的神經系統疾病。而截肢患者現在可以接受互動型植入式義肢，以恢復部分活動能力。研究持續推進，讓植入物的功能更加接近我心目中仿生人（生化）英雄（Bionic Heroes）。
我進入仿生學（Bionics）的旅程始於十年前，當時我受邀前往普芬多夫高等研究院（The Pufendorf Institute for Advanced Studies）。研究院位於瑞典的隆德大學（Lund University），聚集了多元化背景的團隊來探討各種研究主題。我很興奮的是，此次我的訪問主題聚焦於視覺研究，因為它結合了我在物理學與藝術領域的背景。這也讓我有機會聆聽來自其他學科的觀點。我的興趣很快被吸引到設計視網膜用的人工神經元上，其靈感來自生物神經元的碎形幾何結構。
我與隆德大學眼科醫師瑪麗亞·德蕾莎·培瑞茲（Maria Thereza Perez）進行意見激盪討論，深刻意識到當視網膜電路失效時，修復它所面臨的醫學挑戰。佩雷斯描述了電極如何被用來刺激那些不再從受損鄰近神經元接收訊息的神經元產生電訊號。她表示，這個想法其實並不新穎。早在兩個多世紀前，夏爾·勒魯瓦（Charles Le Roy）就曾將電流通入患者的眼睛，使他看到閃光。路易吉·伽伐尼（Luigi Galvani）對青蛙的肌肉使用同樣的方法，使其產生抽動。不過，當時的研究者對身體內部的電路結構幾乎一無所知。神經元的概念是在一個多世紀之後才出現的。
如今，眾所周知，電流是透過突觸（Synapses）從一個神經元傳遞到另一個神經元，就像電流通過電路的電阻器之間一樣。也類似於故障的電阻器，受損的神經元會破壞整個電路的傳導。為了修復電路，現今的外科醫生可以將微型電極植入體內，而不再依賴勒魯瓦和伽伐尼當年使用的粗糙外部導線。
當我在聽培瑞茲的描述時，我感受到了跨領域合作的巨大潛力：物理學家可以帶來他們電網路的專長；化學家提供他們製作電極所需的材料知識；神經科學家則貢獻他們對身體內部相互作用的見解。
這種合作有可能創造出無縫整合於自然神經元之中的人工神經元，形成一個混合系統，就如同1970年代的科幻英雄們從生物學中汲取靈感並融入仿生技術一樣。
神經元的碎形屬性
人類神經元的長度從微米到一公尺不等。它們形成了龐大的網路¬——人類在大腦中每立方公分的神經元之間連結數量，與銀河系中的恆星數量一樣多。維持這些連結的健康對日常活動至關重要。除了促進思考的大腦連結之外，人類也依賴神經元連結眼睛來產生視覺，並連結四肢完成運動。神經元的複雜模式，與手機和電腦的單純電路設計形成鮮明對比。
碎形分支在自然界中很普遍。人體內的支氣管樹（Bronchial Trees）和血管受益於這些結構。分支與其間隙共同形成了兩個共享龐大界面的碎形，藉此在運作性能與相關成本之間取得平衡。神經元利用其分支與空隙的碎形幾何結構來與鄰近神經元建立連結。圖1中的小圖展示了雙極神經元（Bipolar Neuron）的多個視角，該神經元在眼睛的感光細胞（Photoreceptors）與將訊號傳送至大腦的其他視網膜神經元之間，提供了關鍵的連結。這些神經元的樹突（Dendrites）分支呈現碎形結構；當它們自本體向外生長出來時，會在不同尺寸的尺度上產生重複的模式。
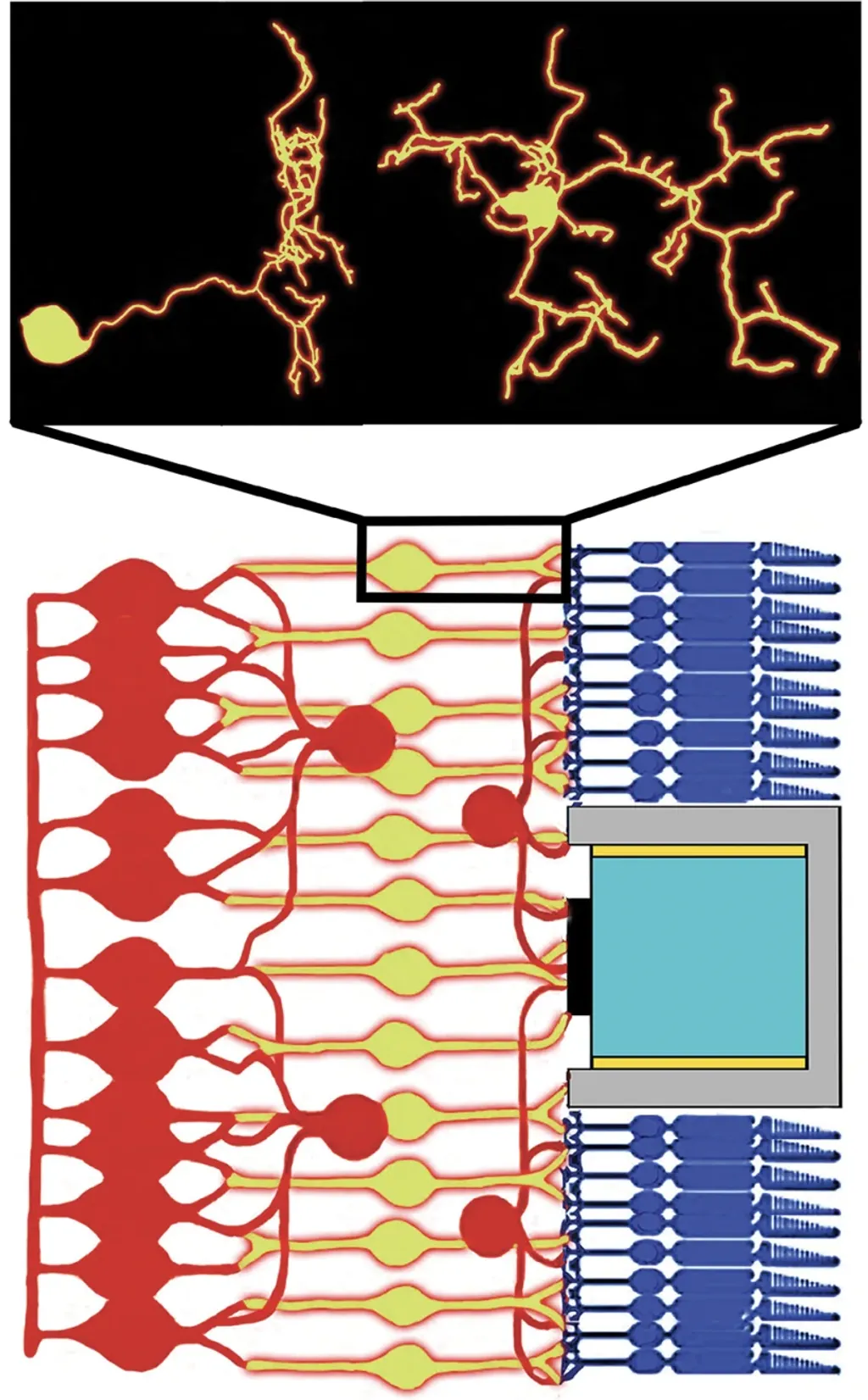圖1. 視網膜線路的側視圖。雙極神經元（黃色）連結到其他類型的視網膜神經元（紅色）、感光細胞（深藍色），以及一個植入的光電二極體（灰色區域及其內部）。為了簡單起見，只呈現出一個光電二極體。小圖展示了一個從兩個角度觀察的真實雙極神經元重建圖。樹突從其圓形細胞核向外分支，延伸範圍達10-20微米。（小圖資料來源：NeuroMorpho.org/CC BY 4.0。）
在自然界碎形當中一個令人驚艷的地方是：只需少數幾次結構模式的重複，就能達到性能與成本之間的平衡之舉。對於某些自然界的碎形而言，模式通常在只有25的放大倍率內重複。對於希望仿造這些幾何結構的生物工程師來說，這是一個好消息：如果分支僅涵蓋有限的尺寸範圍，仿生電極（Bioinspired Electrodes）製造起來將不那麼具有挑戰性。
碎形可分為兩個家族：嚴格碎形（Exact Fractals）與統計碎形（Statistical Fractals）。數學家透過重複模式來精確地構建嚴格碎形。自然界的隨機性破壞了這種精確性，只有模式的統計特性重複。因此，像神經元這類系統中所展現的統計碎形，只會在不同尺度下顯得相似。
圖2a所示的H樹圖案是一種較簡單的嚴格碎形電極範例。大多數關於碎形的討論很快就會聚集在碎形維度D的概念上。在每一個重複層級中，分支數量N與Ｌ-D 成正比，其中L為分支長度。這條冪定律產生了圖案的尺度不變性，而其指數D則決定了L在不同層級間的收縮率。較高的D值對應於較慢的收縮率。因此，D衡量了碎形混合中粗略與細微結構的相對貢獻；當D上升時，細微結構扮演的角色越趨重要。自然界的碎形透過調整其D值來最大化其功能特性，我們的電極也是如此。
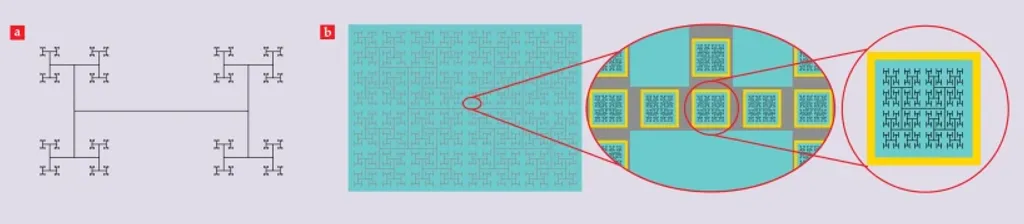圖2. 碎形電極。(a) D值為1.1的H樹示意圖，用以量化分支分裂率。(b)接地電極（灰色）與主動電極（黑色）鍍於光電二極體層（青色）上的示意圖。接地電極與光電二極體的側面皆由絕緣邊界（黃色）隔開。接地電極與主動電極的D值皆為1.9。
走入視網膜
圖2b展示了使用H樹電極從光電二極體陣列收集電荷的設計。一個大型H樹電極被鍍在光電二極體層上。這個大型電極在其分支上設有一系列孔洞。在每個孔洞內，一層絕緣界面將大型電極與光電二極體的側面隔開。在每個孔洞中也嵌有一個較小的H樹電極。當光電二極體受到光照時，其電荷會遷移至表面，由較小的H樹電極收集。該主動電極隨後與較大的接地電極一起產生電場。
圖1說明這種設計在實際應用上的運作方式，圖中展示一個由光電二極體取代患病感光細胞的視網膜下（Subretinal）植入物。這種策略是可行的，因為常見的疾病主要攻擊感光細胞，但鄰近的神經元保持完整，足以與光電二極體的電極接合。理論上，每個主動電極的尺寸會與感光細胞的直徑（約5微米）相當，而接地電極則覆蓋病變區域。
視網膜下植入物體現了仿生學的基本理念——混合系統應該最大化發揮自然功能。來自視網膜下植入物的訊號在會經由視網膜的電路系統傳遞至視神經（Optic Nerve），原則上能受益於數百萬個視網膜神經元所執行的影像壓縮與處理功能。這些功能對視覺至關重要。即便視網膜正常運作，每秒仍有十億個訊號透過視神經傳遞，這要求大腦必須將多達30%的體積用來處理這些進來的資料。失去它的視網膜前哨，大腦的運作將變得吃力。
為了刺激標定的雙極神經元，電極產生的電場會改變穿透神經元表面膜的離子通道（Ion Channel）兩側的電位差。這些通道內被誘發的離子流會沿著神經元的分支觸發訊號。這些訊號隨後會透過神經元表面的突觸連結傳遞給鄰近的神經元。
我們團隊對光電二極體-神經元操作的電性模擬，突顯出採用碎形設計的優勢：大量電荷會停留在H樹的側壁上。與像是格狀、方形的歐幾里得（Euclidean）電極設計相比，碎形長邊界帶來的大面積側壁能產生更高的電容，從而產生更大的刺激電場。我們的模擬顯示這一結果帶來了顛覆性的改變：碎形電極能刺激所有鄰近的神經元，而等效的方形電極只能刺激不到10%。碎形優勢除了能轉化為視網膜植入物更高的視覺解析度之外，也有可能應用於腦部與義肢植入物。
生物親和界面上的碎形集聚
教授我最喜愛的課程——《光、色彩與視覺物理學》（Physics of Light, Color, and Vision）——總讓我想起，植入物的效能強度取決於其最薄弱的環節。學生們經常拿出手機，試圖幫忙地建議我應該將手機鏡頭裝進眼睛。的確，有一些高階相機的像素密度超越了人眼。然而，相機技術並非設計來與生物體系配合的。如果植入物被眼睛細胞排斥，那麼它的電子性能就變得毫無意義了。特別是那些優異的碎形電容也將無從發揮優勢。
神經元的生物相容性（Biocompatibility），即其對外來植入物的耐受性，因此成為所有設計的決定性因素。這些設計原則可以想像成一張三腳凳。最受關注的兩隻腳是電極材料提供的化學環境和物理質地。第三隻腳則是電極的形狀。最終來說，仿生設計應該追求生物親和性（Biophilic）：神經元應該被電極所吸引，而不僅僅是容忍它的存在。碎形結構有可能成為實現這種吸引力的關鍵。
儘管生物工程師通常著重於神經元，但神經膠細胞（glial cells）同樣值得成為研究焦點。作為神經元的維生系統，神經膠細胞提供營養與代謝支持，維持神經元的健康並傳遞訊號。為了賦予我們的電極理想的生物親和性，我們利用神經元和神經膠細胞對人工表面的反應差異來設計。
圖3展示了一個浸泡在神經元與神經膠細胞體外培養液（in vitro）中的電極。我們在二氧化矽（SiO₂）基板上長出以H樹圖案排列的奈米碳管（Carbon Nanotube）。當奈米管自基板上垂直生長時（在圖3中為畫面外方向），便交錯盤結，形成一片具有層次感樹冠的導電森林。神經元會積聚到具紋理的奈米管分支上，因為它們能夠牢固地黏附於類似視網膜多尺度結構環境的表面紋理上。相比之下，神經膠細胞則在間隙中大量增殖，因為較為平滑的SiO₂表面有利於它們的分裂和生長。一旦神經膠細胞集聚在間隙，便不會在物理上阻礙神經元與電極相互作用，但仍然足夠接近以提供神經元必要的健康支援。
圖3. 碎形集聚。螢光顯微鏡（Fluorescence Microscope）影像（中間）顯示神經元（紅色）生長在以H樹分枝模式排列的奈米碳管電極上，神經膠細胞（綠色）則生長在周圍間隙中。上方小圖為神經膠細胞排列的近照。下方為掃描式電子顯微鏡（Scanning Electron Microscope）影像，神經元的細胞核和樹突被分別以藍色和橙色假色顯示。
集聚的現象會隨著細胞累積生長時間而增加，而碎形電極在這方面的效果遠超過歐幾里得電極。特別是，具高D值的H樹可以支撐龐大的神經膠細胞群落，因為其多尺度間隙提供了神經膠細胞在化學上需要貼近神經元，與物理上需要開放空間以進行分裂與生長之間的最佳平衡。富含神經元的分支也能因此蓬勃發展，因為其與間隙的長碎形邊界能提升神經膠細胞群落帶來的健康效益。
那些活躍的神經元隨後會最佳化它們的網路。在經歷初期樹突的爆發性生長以建立連結後，神經元聚集成更大的叢集，並縮減其中一些連結。從結構上來說，這種最佳化類似於小世界網絡（Small-world Networks）——一種使用相對較少的連結連通所有位置的高效率系統。你可能已經從航空公司使用的樞紐系統中體驗過小世界網路。不是任意兩個機場之間都有直飛航班，但可以透過主要樞紐到達需要去的地方。所幸，自然界的神經元表現得更好。
碎形共振
成功引導神經元到電極上之後，我們的合作團隊提出，碎形共振（Fractal Resonance）可以更進一步幫助神經元茁壯成長。我們的假設是，將電極與神經元的精確碎形特徵相匹配，會促進兩者之間更大的連結性。雖然H樹具有自然界碎形的多尺度特徵，但其直線條與90度轉角的高度重複，與仿生明顯不符。
我們透過分析來自視網膜（雙極神經元）和大腦（海馬迴神經元，Hippocampal Neurons）兩種神經元的實例，發現它們的樹突在空間中交織的方式，是產生其統計碎形模式的關鍵。神經元對這種碎形交織行為的趨向，引發了一個根本性的問題：偏離自然碎形形式的負面後果是什麼？如果神經元功能因此衰退，那麼碎形共振就應該成為所有電極設計的主導原則。
為了給出答案，我們創造了自然界沒有的神經元，使用共軛焦顯微鏡（Confocal Microscopy）對神經元成像，然後數學性地扭曲它們的樹突交織角度。在圖4中，中間的神經元是自然狀態，左右兩側的神經元則是分別經由拉直與捲曲樹突產生的變形。這些變形導致神經元的D值分別向相反方向偏離自然值1.42。持續捲曲的過程最終將產生一個三維球體，其細微結構填滿整個體積。相反地，若將分支完全拉直並首尾相連，則會產生一條平滑的一維直線，完全缺乏細微結構。
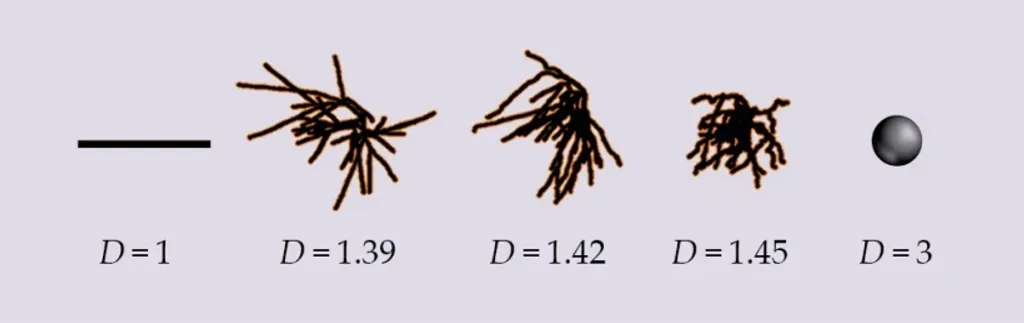圖4. 神經元的形狀經過最佳化，以平衡其連結性與連結成本。為了展示D值的範圍，將一個自然海馬神經元（D值為1.42）與兩個變形神經元以及D值在低和高時會呈現的歐幾里得形狀進行比較。
提高D值會增進神經元與鄰近細胞溝通的能力，因為連結密度也隨之提升。這可以量化神經元在給定體積中的實體分佈，從而衡量樹突表面上突觸暴露量的增加。然而，神經元需在提升連結密度與建構及維持這些連結的成本之間權衡。建構成本包括給定體積內的樹突總量。維護成本則包括運作離子通道所需的能量，而這隨特定體積內樹突表面積的增加而提升。
關鍵在於，連結性及其成本隨D值的上升以不同速率增加，這使得神經元能夠平衡這些相互競爭的因素。這種平衡可利用平衡連結性（Balanced Connectivity）來量化，該指標納入連結速率與成本速率的比值。不出所料，自然神經元的D值集中在平衡連結性曲線的峰值附近；大自然體現了最佳的細微結構量。
變形神經元的D值偏離峰值，而平衡連結性的下降則量化了偏離神經元自然形態的相關退化。歐幾里得形狀同樣遠離最佳平衡，這說明了為何神經元遵循碎形而非歐幾里得幾何結構。球體內缺乏間隙會產生龐大的分佈範圍，但其高質量密度所付出的高昂代價，解釋了為何神經元不是那樣的形狀。簡單筆直的線條在局部位置的質量耗用低，但它們要付出讓其分佈範圍分散到廣闊區域的代價。
如果電極的D值與神經元的相匹配，神經元在黏附過程中便能保留其自然的交織結構。如此一來，神經元在與鄰近神經元及電極互動時，便能受益於處於平衡連結性峰值的優勢。相對地，若強迫神經元沿著歐幾里得電極（如網格）的直線生長並在尖銳的轉角處轉向，則會迫使神經元滑落至平衡連結性曲線的下坡。
碎形共振可以比擬為最後進場著陸的飛機。當機師接近一維直線跑道時，傾向筆直飛行；而神經元則喜歡附著在我們的電極時保有其交織結構。最終，不同類型的神經元或許可以依據其D值被引導到不同的電極跑道上。我們正在開發運用類似自動駕駛的軟體，來預測能與樹突最大程度重疊並最小化其變形的電極形狀。這些統計碎形電極將來會用3D列印技術製造，以用於未來的臨床試驗。
碎形仿生學的美麗新世界
碎形帶來的好處能為我們帶來多大的進步？用於替代受損感光細胞的開創性植入物，僅有4%的正常視覺敏銳度（Visual Acuity）。這比10%的法定失明標準還要差，低於這個標準就無法安全地從事如駕駛等活動。那些原始視網膜下植入實驗用的方形電極，電容都很低。它們無法產生大範圍的激發電場，而且附著在電極表面的少數神經元很可能發生變形，這阻礙了它們有效地將訊號傳遞給鄰近的視網膜神經元。
相比之下，我們模擬出的碎形植入物預期能達到約25%的敏銳度。我們製作了20微米大小的光電二極體，比感光細胞略大，以彌補其較差的性能，由此產生的視覺足夠準確，可以執行許多日常任務。圖5比較了這兩種敏銳度水準與自然視力，使用我老朋友格里芬（Griffon）像素密度逐漸降低的照片。
圖5. 我的德國剛毛指示犬（German Wirehaired Pointer）格里芬的照片。照片的解析度經過調整，以象徵不同程度的敏銳度，並與20/20標準視力比較：100%（左）、25%（中）和4%（右）。法定失明相當於10%的敏銳度。視網膜下植入物過往提供4%的敏銳度，但新型設計採用碎形結構，以更好地匹配其所連結的神經元設計，預期可帶來25%的敏銳度。
我最近回到普芬多夫研究院，與佩雷斯一起回憶了我們的仿生學探險。我們同意將我們的人工神經元重新標註為「互連結構（Interconnects）」，以囊括其多重功能，這些功能超越了僅稱它們為「電極」隱含的電性表現。例如，讓樹木在風中搖曳而不折斷的多尺度分支特性，可以轉譯為機械可撓性電子元件——互連結構可以貼合視網膜形狀，外科醫生甚至可以將它們捲起來，透過侵入性較小的插入方式輸送。運用碎形形狀操控奈米尺度光線的進展，甚至可能實現色覺所需的波長調控。
奠基於固態晶片（Solid-State Chip）的革命，電子方案持續是視網膜修復的明確策略。雖然我的研究專注於互連結構，但其他進展——例如改良的光電二極體或補充性可植入電池——也可能來自植入物的電源。另一種長遠策略則著重於製造有機人工感光細胞，或利用幹細胞（Stem Cell）培養新的生物系統。無論何種方法，未來的進展都將需要生物工程師與神經科學家之間的合作，以加深對自然系統與植入系統交互作用的理解。目前已展開的跨領域工作，已充分凸顯自勒魯瓦與伽伐尼的開創性實驗以來，這一領域迄今所取得的巨大進步。
感謝我的合作夥伴：Benjamín Alemán、John Dalrymple-Alford、Bruce Harland和Maria Thereza Perez，以及我現任與過往的博士生：Bret Brouse、Aiden Dillon、Saumya Keremane、Rick Montgomery、Saba Moslehi、Sam Philliber、Conor Rowland、Julian Smith和Bill Watterson。
參考文獻
►J. B. Bassingthwaighte, L. S. Liebovitch, B. J. West, Fractal Physiology, Springer (1994).
►E. R. Kandel et al., Principles of Neural Science, 6th ed., McGraw Hill (2021).
►L. N. Ayton et al., “An update on retinal prostheses,” Clin. Neurophysiol. 131, 1383 (2020).
https://doi.org/10.1016/j.clinph.2019.11.029
►S. Moslehi et al., in The Fractal Geometry of the Brain, 2nd ed., A. Di Ieva, ed., Springer (2024), p. 849.
►C. Rowland et al., in The Fractal Geometry of the Brain, 2nd ed., A. Di Ieva, ed., Springer (2024), p. 877.
本文感謝Physics Today (American Institute of Physics) 同意物理雙月刊進行中文翻譯並授權刊登。原文刊登並收錄於Physics Today, Dec. 2024雜誌內 ( DOI: 10.1063/pt.wrls.ugye )。作者: Richard Taylor。中文編譯：劉雨恩，國立台灣大學物理系學生。
Physics Bimonthly (The Physics Society of Taiwan) appreciates Physics Today (American Institute of Physics) authorizing Physics Bimonthly to translate and reprint in Mandarin. The article is contributed by Richard Taylor and was published in (Physics Today, Dec. 2024; DOI: 10.1063/pt.wrls.ugye ). The article in Mandarin is translated and edited by Y. Ｅ, Liu, studying at the Department of Physics, National Taiwan University.
