
「功能定理」是一項很讓人困擾的主題,本專欄曾探討「 跑步機上的功與能 」,詳細剖析了,為何跑者原地不動,仍需耗費能量對輸送帶作正功?本單元,讓我們進一步探討簡單機械的「功能定理」,包含:滑輪、槓桿、及滑車,所涉及的 作功 及 能量變化 。
小試身手
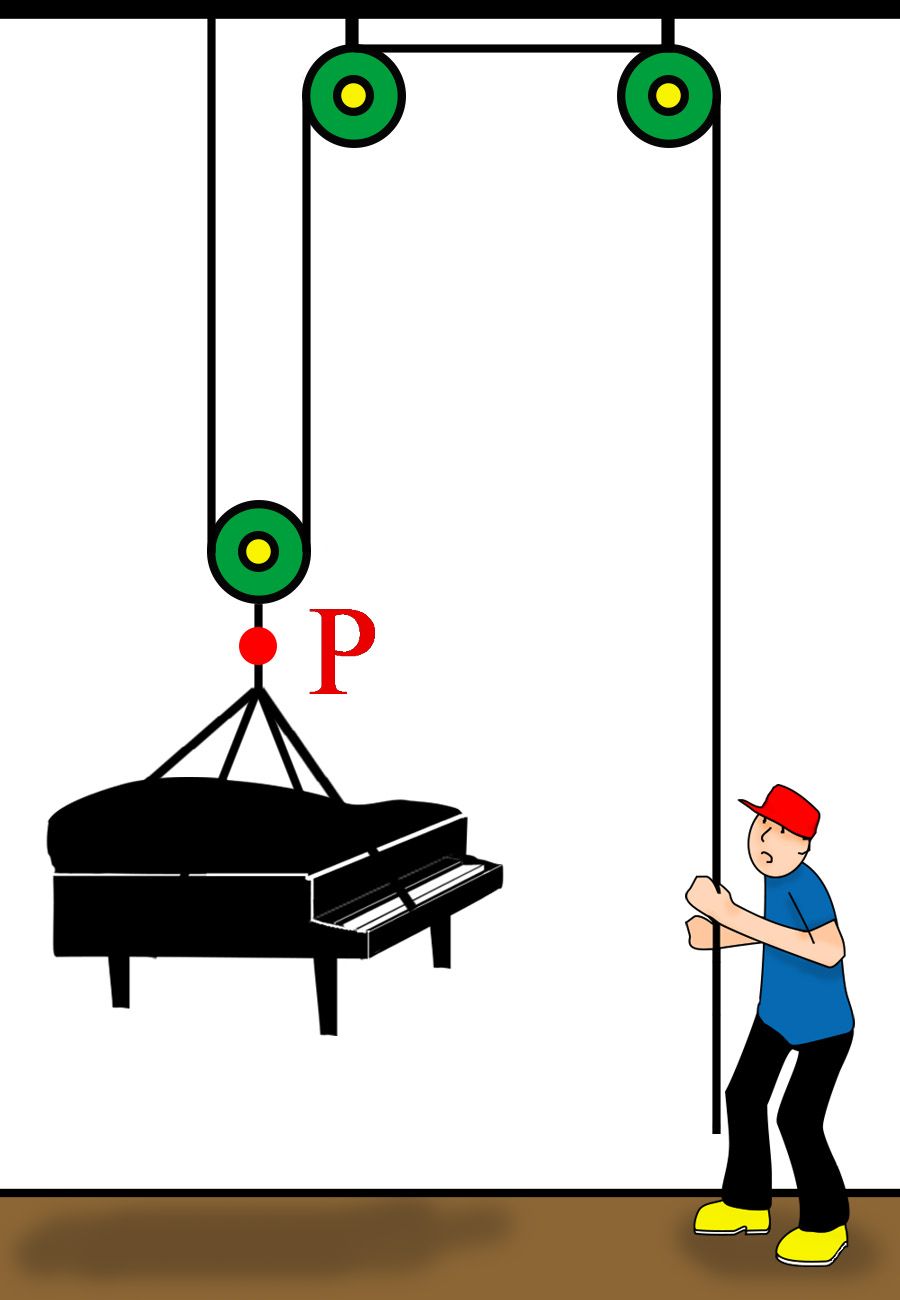
圖1:滑輪的力與作功
1. 有一個人以700N的力向下拉繩子,在另一端有一台重1200N的鋼琴(如圖1),忽略滑輪質量,則鋼琴上繩子的 P點 張力為多少N?
(A)200 (B)700 (C)1200 (D)1400 (E)2600
2. 承上題,當鋼琴移動了2.0m的過程中,此人對鋼琴所作的功為何?
(A)1400J (B)2400J (C)2800J

圖2: 槓桿的力與作功
3. 承上題,此人對鋼琴所作的功(W),與鋼琴所增加位能(圖4: ∆ U)的關係,應如何?
(A)W > ∆ U (B)W < ∆ U (C)W = ∆ U
4. 根據圖2,為了提起左側重量為F g 之重物,人至少需施力(F)於槓桿之右側,則F g 與F之大小關係為何?
(A)F > F g (B)F < F g (C)F = F g
5. 承上題,若以最小能抬起重物的外力F,將物體抬起h高度,則此外力對物體作功(work)應如何?
(A)work > F×h (B)work < F×h (C) work = F×h
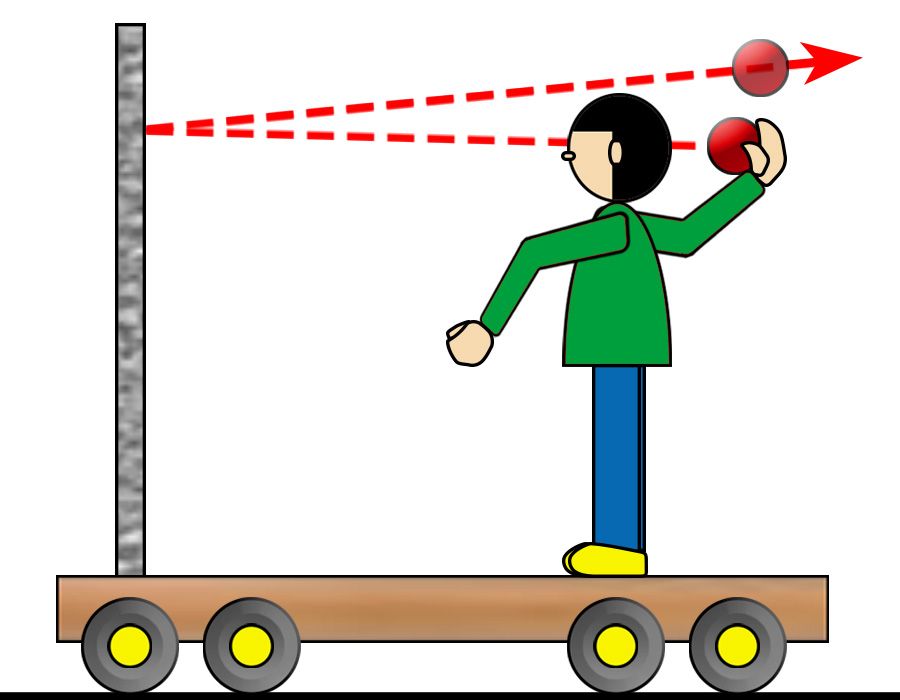
圖3: 丟球驅動滑車
6. 承上題,重物所增加的位能( ∆ U),與外力作功(work)的大小,關係如何?
(A) ∆ U > work (B) ∆ U < work (C) ∆ U = work
7. 如圖3所示,一人站在靜止的滑車上,將手上的皮球丟出。皮球彈到滑車的牆上後,滑車會向左運動,而球則反彈向右飛出。則[滑車+人]所獲得的動能(E k人+車 ),與此人的手對球作功(W 手→球 )的關係為何?
(A) E k人+車 > W 手→球 (B) E k人+車 < W 手→球 (C) E k人+車 = W 手→球
8. 承上題,皮球撞擊滑車牆壁的過程,兩者間的正向力,分別對滑車及對皮球,所作的功應如何?
(A)對滑車作正功、對球作負功 (B)對滑車作負功、對球作正功
(C)皆作正功 (D)皆作負功 (E)皆不作功

圖4: 推牆後退
9. 如圖4,一人靜止站在滑車上,以手推牆壁使自己加速後退,則此人所受牆壁的正向力作功,應如何?
(A)作正功 (B)作負功 (C)不作功
10. 承上題,人的腳與滑車之間的摩擦力,分別對人及車的作功,應如何?
(A)對人作正功、對車作負功 (B)對人作負功、對車作正功
(C)皆作正功 (D)皆作負功 (E)皆不作功

