2024年的諾貝爾物理學獎頒給了加拿大多倫多大學的Geoffrey Hinton和普林斯頓大學的John Hopfield，表揚他們在人工神經網路與機器學習領域的開創性工作。瑞典皇家科學院的這個決定，在物理界引起了軒然大波，贊成跟反對的人展開了激烈的辯論，可以說是2024年最具爭議性的科學新聞了。到底物理學家們是在吵什麼呢？

 

諾貝爾物理學獎自1901年設立以來，一直被視為物理學界的最高榮譽。歷年來該獎項的內容，不外乎基礎物理理論的突破，以及以基於物理學的實驗技術創新來解決重大的科學問題（就算解決的不是物理問題也可以）。早期的諾貝爾獎剛好與量子力學大革命的歷史重疊，許多獲獎者都是改寫近代物理學超級巨星，這也讓諾貝爾獎的光環增色不少。對物理學家而言，諾貝爾物理學獎的獲獎者等於是要將名字與普朗克、愛因斯坦、海森堡、薛丁格等人並列刻在桂冠上，如果不是超級頂尖的物理學研究，物理學家可是不會服氣的喔！

 

所以，要弄清楚這次的爭議，就得從弄清楚獲獎者的研究內容開始：「這是超級頂尖的物理學研究嗎？」

 

Hopfield是正牌的物理學家，還擔任過美國物理學會的會長。回顧他在得獎領域的研究，就是在人工智慧發展史上知名的「Hopfield network」，是現代類神經網路與深度學習的先驅。這個研究始於1980年代初期，他提出的問題是：「我們是不是能弄清楚人類大腦記憶方式的物理原理，並且將之移植到電腦晶片上？」這大概是每個研究腦科學的物理學家會問的問題，如果做得到的話，就可以做出真的能模仿人腦的電腦了。

 

現在的電腦都是所謂的「馮紐曼架構」，是由出身匈牙利的數學家兼物理學家約翰‧馮紐曼（John von Neumann）所提出，主要的特徵是「處理器」與「記憶裝置」（包含記憶體與硬碟）是分開的，不論是程式或是資料，都是儲存在記憶裝置中，運算時送到包含控制單元與邏輯與運算單元的中央處理器進行。在此架構中，每一組「記憶」（文字、聲音或影像）都必須精確記錄在記憶裝置上特定的區塊，如果要在同一個區塊上寫入另一組記憶，就得先把原來的記憶刪除才行。因此，我們才會經常遇到「手機記憶體不夠用」的問題。

 

人腦顯然不是採用這種方式，在大腦裡頭並沒有特定的區域是專門用來儲存我們讀過的文章或是看過的影像，而且我們在取出記憶時，也不是像電腦一樣直接存取與「原版」百分之百相同的精確內容。因為人腦的記憶是透過大腦神經元之間的連結強度儲存，所有的神經元連結構成了一個複雜的腦網路。當一個記憶被觸發時，一開始可能只有少數神經元開始活躍，接著神經電訊號根據神經元間的連結強度觸發了一連串的神經元迴路活動，讓我們把記憶重建起來。這種方式跟現代電腦記憶資料的方式完全不同，更像是這兩年當紅的「生成式人工智慧」（generative AI），如生成文字的ChatGPT、以及生成圖片的diffusion model等。

 

Hopfield在1982年的論文中所提出的，就是模仿大腦這種記憶機制的類神經網路模型，來模擬記憶的形成與重現，稱之為「關聯式記憶」（associative memory）。這個模型與統計物理學中探討磁性的Ising模型密切相關，我們用圖一這個簡單的例子來說明Hopfield model 如何運作。

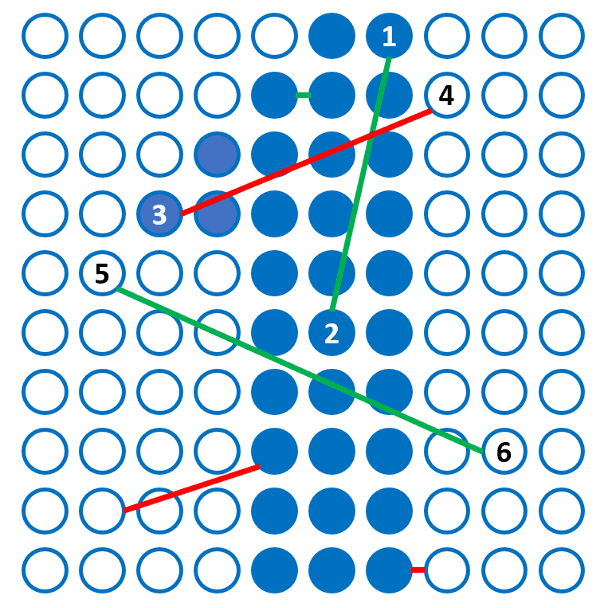
圖一：Hopfield 模型的訓練資料。

圖一是排列成10×10方陣的100個神經元，每個神經元有「放電」（藍色）與「休眠」（白色）兩個狀態，可以用來表示一張10×10畫素的圖形，此圖為數字「1」。如果是傳統電腦的記憶方式，這100個神經元記錄了「1」之後，就得要持續保持圖中各個神經元的狀態，如果要存其他圖形，就得要把組態更新，原來的「1」就被「忘記」了。Hopfield的想法則是改用神經元之間的連結來記憶這張圖，採用的方式是神經科學中的Hebb’s rule：「兩個神經元動作一致，連結會增強；否則連結會減弱」。以圖一為例，w_ij為第i與第j個神經元之間的連結強度，一開始全部設為0，然後檢驗圖中的兩兩畫素，數值相同者將w_ij增加1（如圖中的神經元1、2同時放電；5、6同時靜止，故w₁₂ 與 w₅₆ 都從0→1），數值不同者則不變（w₃₄ 維持為0）。檢查並更新所有的 w_ij 後，這張圖就訓練完成了。接著可以訓練其他資料，例如排列為「0」跟「2」的圖形，根據上述的方式來更新神經連結強度，整個神經網路就訓練完成，此時 w_ij 的可能數值會是0～3之間的數字。這裡要注意的是，這三個數字圖形的特徵，是同時儲存在這些神經元的連結中，混合在一起的。 

 

接下來定義一個能量函數：

其中  為第  個神經元的狀態，其值為1（放電）或 -1（休眠）。  的初始組態表示這個神經網路所受到的外界刺激輸入，接著這個神經網路會依以下的規則更新其組態：

 

1.     從神經網路中隨機選一個神經元

2.     將 ，重新計算能量

3.     若新的能量比原能量低，則接受  為新組態，否則仍保持原來的狀態

4.     回到 1.

 

重複上述步驟，直到能量不再降低為止，即為輸出之組態。我們可以先用這個網路看過的「0」、「1」、「2」這三張圖作為輸入，經過上述步驟後發現，可以正確的將「原圖輸出」，也就是這個神經網路的確有「記住」這三張圖。這個任務看似簡單，但是並沒有那麼理所當然會成功，因為在我們的神經網路裡，三張圖的特徵資訊是混合在一起的。根據Hopfield的研究，一個神經網路能夠「記住」的資料數量，大約是「神經元數目×0.15」，即這個100個神經元組成的網路，可以記住15張圖的特徵。

 

接下來的測試就比較有趣了，我們輸入一張加入了雜訊的「1」，經過上述步驟後，神經網路輸出了乾淨的「1」，這就像我們看到暈開的筆跡時，還是可以辨識出寫的是哪個字，這是「忠實記憶每個畫素」的傳統電腦記憶方式所辦不到的（圖二）。

 

當然這個簡單的神經網路也不是萬能的，我們如果輸入它沒看過的數字「8」圖形，這個網路會輸出在它的記憶中，特徵比較接近的「0」。其他隨機的輸入，也有可能輸出「看似有些數字的特徵，但是四不像」的圖形。

圖二：Hopfield網路可以「去除雜訊」。

我們可以用物理的觀點來理解Hopfield網路的能力與限制，上述的神經元組態以及能量函數，其實跟統計物理中研究「磁性」以及「自旋玻璃」（spin glass）系統的「Ising模型一樣」。神經元的「放電」與「休眠」兩個狀態，可以類比於電子「向上」與「向下」的自旋狀態，而神經元之間的連結強度 w_ij 則是自旋之間的磁交互作用。磁性或自旋玻璃材料的 w_ij 取決於材料特性，而神經網路的 w_ij 則由學習或訓練過程決定。不管是哪一種，在 w_ij 確定後，「能量地景」（energy landscape），也就是「組態對能量的關係圖」就決定了。

圖三：能量地景示意圖，橫軸為組態，縱軸是能量。組態為高維度空間，無法在平面圖上表示，故僅以一個維度代表。

如圖三所示意，訓練過程會讓能量地景中，排列為「0」、「1」、「2」的組態（紅框）為局部極小值，所以附近的組態會在更新過程中逐漸往這些局部極小值收斂，因此可以達到圖二中「除雜訊」的結果，但是對於不在訓練資料內圖形如「8」，在這個能量地景中沒有對應的能量低點，結果就「滑」到「0」的局部最小值去。此外，訓練過程中也會出現一些「副產品」如圖三中的黑色框圖形，在那附近的組態如「4」最後收斂到這個圖形。

 

Hopfield的工作，將腦科學、物理學與人工智慧連結了起來，物理學家與Ising模型交手甚久，也有相當深入的瞭解，由這個切入點著手，有機會讓物理學家更能掌握大腦的秘密；另一方面，這麼簡單的類神經網路模型，就可以展現出關聯式記憶的形成與取出的能力，這也對當年陷入冷凍期的人工智慧領域注入了新的活力。

 

Hinton人稱「人工智慧教父」，剛於2018年獲頒「資工界諾貝爾獎」之稱的圖靈獎。他沒有物理學相關的學經歷背景，但是將Hopfield的模型進一步改進，引入了更深入的物理學與腦科學概念。首先是「隱藏層」：在Hopfield的模型中，輸入、處理與輸出都是同樣一群神經元，但是大腦的運作顯然不是如此：輸入是感官系統、輸出是運動系統、而處理則是在大腦的中樞。Hinton將Hopfield網路的神經元稱為「可見層」，再加入一群神經元來代表中樞神經的「隱藏層」，然後在訓練網路（決定 ）以及更新組態時引入「溫度」的概念。Hopfield的演算法是溫度等於0，一切都以最低能量為準，加入了溫度後讓神經網路更具有彈性，可以得到更好的結果，Hinton將這個新的模型稱為「玻茲曼機器」（Boltzmann machine）。

 

然而把網路與演算法複雜化的代價是計算曠日廢時，於是Hinton簡化了這個網路，將同一層神經元之間的連結全部移除，只留下可見層跟隱藏層之間的連結，這一招雖然就腦科學的角度來看沒什麼道理，不過確實有用——計算效率大幅提昇，而且結果也沒有因網路簡化而變差。Hinton將這個修剪過的網路稱為「受限玻茲曼機器」（restricted Boltzmann machine）。

 

既然計算效率提高了，何不增加更多的隱藏層呢？當然加！果然結果越來越好！由於加了很多隱藏層，網路就變「深」了，開啟了近年來大放異彩的「深度學習」領域。

 

尤以上的介紹可以看出，物理學的確在人工智慧與深度學習的領域中有不小的貢獻，不過目前的機器學習技術在訓練神經網路時，已經不再採用熱力學與腦科學的概念，而是用效率更高的方式，例如「逆向傳播」（backpropagation）法，所以要說「現在的人工智慧技術已經跟物理學沒什麼關係」也沒有不對。但是隨著硬體晶片的能力不斷提升，人工智慧能做的事也越來越多，各國大型科技公司競相建立大型的超級電腦、吃掉大量的能源來跑這些神經網路程式，如果回歸Hopfield「向自然界學習」的初心，人腦只需要20W左右的功率就可以運作，物理系統自然而然就會跑到複雜的高維能量地景中的極小值，看起來實在比動輒數以萬計的高速運算GPU卡全力運行輕鬆太多了。所以也許不久之後，這個領域又要回到Hopfield所設定的軌道上也說不定。

 

行文至此，相信各位讀者對於「2024的諾貝爾物理獎到底有沒有道理」這個問題，應該也有了自己的答案了吧！