量子行走 （Quantum Walk）
量子行走（Quantum Walk）是隨機行走（Random Walk）的量子版本，它描述量子粒子在圖（Graph）上的移動方式。然而，與隨機行走的古典粒子不同，量子行走的粒子可以同時沿著多條路徑移動，並利用量子疊加（Superposition）和干涉（Interference）效應。這意味著量子行走中的粒子可以同時存在於多個位置，而其最終位置的機率分佈則取決於不同路徑之間的干涉結果。由於這種特性，量子行走在設計更快速的量子演算法中發揮了重要作用，特別是在搜尋和排序問題中，往往能夠比隨機行走更高速有效。
圖一: (a) 隨機行走的粒子只能選擇左或右的一種路徑。(b)直到最後測量之前，量子行走的粒子可以同時以機率分布形式出現在左或右兩種路徑之中。兩種行走方式的不同會影響到最後在不同位置的機率分布形式。隨機行走符合擴散形式，而量子行走則可超過擴散速度。
Grover 量子演算法可以視為量子行走的一種應用，Grover 演算法考慮粒子在完全圖（Complete Graph）上的行走，並利用量子疊加與干涉來加速搜尋目標狀態。本質上，Grover 演算法是一種特殊的量子行走，它在狀態空間中運行，並透過振幅放大（Amplitude Amplification）機制來提高目標狀態的出現機率。在這個過程中，初始狀態是所有可能狀態的均勻疊加，類似於量子行走中粒子同時分布於多個位置。演算法透過天諭（Oracle）操作來選擇性地改變目標狀態的相位，接著使用擴散（Diffusion）操作來增強目標狀態的振幅，這相當於控制粒子在狀態空間中的行走路徑。透過這些步驟，Grover 演算法逐步將概率集中到目標狀態，使搜尋過程比古典方法更快，達到O(√N)的時間複雜度，而古典搜尋需要O(N)的時間。
量子隨機行走 （Quantum Stochastic Walk）
想像你正置身於一座城市中，四周是錯綜複雜的道路和高樓大廈，而你要找到從起點穿過這座城市到達目的地第一條最快捷路徑。因為你可以利用量子力學，所以你不用像古典粒子般的一條條路慢慢嘗試錯誤，而可以同時利用量子機率波探索所有可能的路徑。但是這座城市的環境卻一直在變化而不是完全平靜不變的。例如炎熱的天氣讓地面微微顫動，空氣中的水蒸氣扭曲了你的視線，讓原本清晰的路徑變得模糊甚至扭曲起來，因此影響了你的路徑搜尋速度。這些環境的影響造成的擾動讓你的行動不能維持在純粹量子行為，而是隨時與環境進行著複雜的各種交互作用，因而在量子機率波內也引入了古典的隨機性。這種量子與古典交互作用的特性就是量子隨機行走（Quantum Stochastic Walk）的特徵行為。在量子隨機行走中，這些古典系統的效應會造成量子系統的去相干現象，進而模擬了量子系統中的粒子與古典環境的能量與資訊的交換，使得粒子在量子系統內的行走不僅僅受到量子疊加和干涉的影響，還受到環境溫度或能量漲落的干擾。這種特殊模型不僅描述了量子系統在現實條件下的演化，也成為理解自然現象和設計量子技術的重要工具。
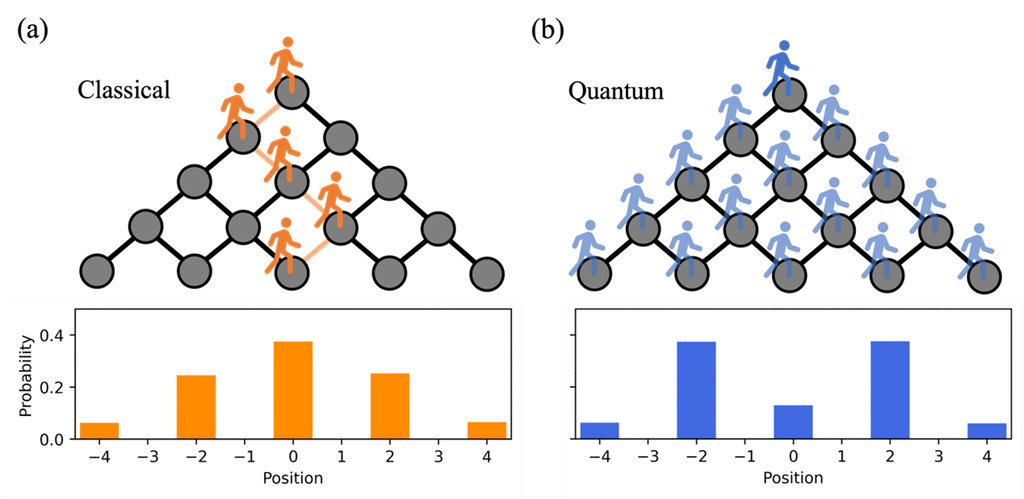
量子隨機行走是結合隨機行走和量子行走的物理互動模型，可以用來模擬開放量子系統（Open Quantum System）中的動態行為。量子隨機行走同時考慮了古典隨機行走的機率擴散特性和量子行走中的量子力學現象（如疊加與干涉），在這個模型中，我們考慮準靜態(Quais-static)的環境，也就是說環境龐大到不受目標系統的影響。環境的影響通常可以用Dephasing和Damping來描述，因為這兩個現象反映了量子系統與環境之間的不同交互方式。Dephasing主要描述量子系統在與環境交互影響後失去相位訊息的過程，導致量子干涉效應消失，系統逐漸表現出古典行為，這通常與環境中的隨機漲落或雜訊相關。在這個過程中，量子系統的狀態和環境的狀態會糾纏在一起，導致量子態的相位也變得隨機。想像你在一個安靜的湖面上扔了一顆石頭，湖水會形成一圈圈的波紋，這些波紋之間會產生干涉現象。如果這個時候突然刮起了一陣風，湖面變得波濤洶湧，原本的波紋就會被擾亂，最後看不出任何規律。Dephasing像這陣風一樣，會打亂量子系統中的相位，使原本有序的量子干涉圖樣消失而變得混亂，逐漸看不出原來的干涉圖樣，並讓系統看起來像是古典的隨機狀態。Damping則描述量子系統與環境耦合時，量子系統中的激發能量會通過這種耦合轉移到環境中，導致量子系統的激發態逐漸向基態過渡，能量耗散在環境中，這是一個不可逆的過程。例如，一個振動琴弦在空氣中振動幅度逐漸減少而逐漸失去能量，最終靜止不動。這種阻尼現象在開放量子系統中也存在，會導致量子狀態隨時間指數衰減，降而使得量子糾纏減少，甚至最後消失。這兩種效應共同解釋了量子系統在環境影響互動下如何失去其量子特性，從而過渡到古典行為。簡單來說， Dephasing描述量子系統逐漸失去疊加態的性質，如圖二（a）所示。圖二中描述一個量子位元（系統）因為環境的影響而從疊加態|├ +⟩=(|├ 0⟩+|├ 1⟩)/√2逐漸變成古典的機率統計（50%處於|├ 0⟩，50%處於|├ 1⟩）。在運動過程中，每步過程中有機率p會發生Dephasing而逐漸降低處於狀態|├ +⟩的機率。可以注意到，當機率p越大時，降低的速度越快。而當機率p為零時，量子位元可以一直保持在疊加態|├ +⟩；另一方面，Damping描述能量的流失或轉移；如圖二（b）所示。圖中描述一個量子位元因為環境的影響從狀態|├ 1⟩（激發態）變成|├ 0⟩（基態）。在運動過程中，每步過程中有機率p會發生Damping而導致量子位元處於狀態|├ 1⟩的機率逐漸降低。
與其他開放式量子系統模型相比，量子隨機行走有個重要特徵是可以調整古典與量子行為間的權重（ω），從而模擬不同權重下的行為。也就是說，當環境的影響較弱時（ω≈0），系統更接近量子隨機行走，而相反的，當環境的影響較強時（ω≈1）則更類似隨機行走。這使得量子隨機行走在物理模擬與數值分析領域都有重要應用，例如解釋光合作用中能量的高效傳遞，幫助分析和排序大規模網絡中的節點（如量子頁面排名），甚至利用開放量子系統的類比模型來設計更高效的量子演算法。因此量子隨機行走不僅深化了對開放量子系統的物理理解，更提供了一種將量子物理與古典計算結合的新視角。
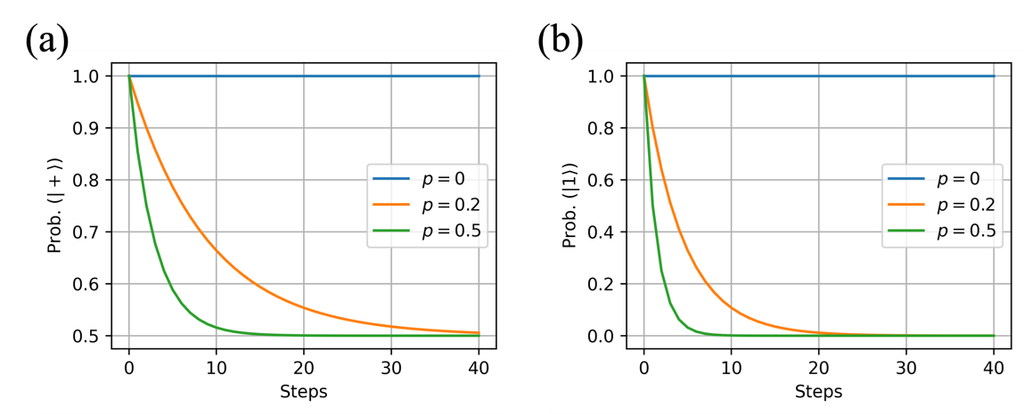圖二: （a）一個量子位元的Dephasing過程，量子位元會由一開始的疊加態|├ +⟩=(|├ 0⟩+|├ 1⟩)/√2逐漸變成古典的機率統計（50%處於|├ 0⟩，50%處於|├ 1⟩），因此處於疊加態|├ +⟩的機率也會逐漸降低（p為每步演化過程中發生Dephasing的機率）。 (b) 一個量子位元的 Damping過程，量子位元會從狀態|├ 1⟩逐漸變成|├ 0⟩，因此處於狀態|├ 1⟩的機率也會逐漸降低（p為每步演化過程中發生Damping的機率）。
量子隨機行走的數學模型
量子隨機行走可以用數學模型，例如林德布拉德主方程（Lindblad master equation）或Kraus 運算子（Kraus operator）來模擬。首先，林德布拉德主方程模型是一種用於描述開放量子系統的常用模型，其理論基礎最早由芬蘭物理學家 Göran Lindblad 在1976年提出，特別適合於與環境進行Markovian交互的量子系統。Markovian特性指的是系統的演化僅依賴於當前狀態，而不涉及過去的歷史，也就是說，系統在每一個時間點的行為只與當前的狀態相關，而不受先前狀態的影響。這樣的假設極大地簡化了系統的數學描述，使其成為一個無記憶性過程（Memoryless process）。Markovian交互意味著系統和環境之間的影響迅速消散，因此不會產生長時間的記憶效應。該方程以密度矩陣的形式表示系統的演化，並包括兩個部分：一個是系統內部的哈密頓量作用，另一個是與環境的相互作用，通常透過林德布拉德運算子（Lindbladian operator）來描述。這些算子描述了Dephasing和Damping等現象，是對量子退相干和耗散過程的數學描述。另一方面，Kraus運算子是一種描述開放量子系統演化的重要工具，特別適用於處理離散時間的量子過程。根據Kraus表示定理，任何開放量子系統的演化都可以表示為一組Kraus運算子的作用，這些運算子滿足某種完備性條件，對量子態的演化進行更新，確保量子態的規範性。
儘管Kraus運算子和林德布拉德主方程都是用來描述開放量子系統，但它們適用的情境不同。林德布拉德主方程適用於連續時間的演化，尤其是在Markovian環境下。林德布拉德主方程描述了系統內部哈密頓量的作用以及與環境的相互作用。可以看作是Kraus運算子在連續時間極限下的推廣。當時間步長趨近於零時，Kraus運算子的作用會導致一個連續的、微分形式的演化方程，即林德布拉德主方程。因此，Kraus表示和林德布拉德主方程在本質上描述的是同一種量子系統的演化，但在不同的時間尺度和假設下使用不同的數學形式。特別是在量子計算和資訊處理中，Kraus運算子扮演著描述開放量子系統非么正演化（Non-unitary evolution）的重要角色。然而，為了在量子電腦上實際操作，這些運算子必須轉化為具體的量子電路形式。Kraus運算子的作用可以通過引入輔助量子位元（Ancilla qubits）來模擬，這些輔助量子位元扮演著環境的角色與量子系統互動。透過設計輔助量子位元與系統位元的交互作用，我們可以作用Kraus運算子於系統之中。也就是說，每個Kraus運算子對應一個么正算符（Unitary operator），透過對輔助量子位元做測量，我們可以在量子系統之中引入古典的機率。
光合作用
在光合作用過程中，由發色團（Chromophore）與蛋白質結合形成的捕光複合體（Light-harvesting complex）會吸收光子並將能量傳遞到光合反應中心（Reaction Center），再將太陽光能轉化為化學能，供植物、藻類和某些細菌使用。這一過程中，捕獲的光子能量會以電子激發態的形式（激子）傳遞到反應中心。研究發現，這種能量傳遞的效率極高，甚至接近 100%。量子隨機行走常被用來解釋這種高效傳遞的原因。量子隨機行走同時考慮量子力學的疊加效應和干涉效應，使得能量可以在所有可能路徑上同時「探索」，從而快速找到最短或最佳的傳遞路徑。同時，量子隨機行走也將環境的影響納入考量。在傳遞能量的過程中，周圍的分子環境提供了一定程度的隨機漲落（類似熱擾動）。這些環境影響會導致Dephasing，而使得量子系統逐漸失去其量子疊加態，變得更像一個古典隨機過程。然而，適當的去相干程度可以避免干涉圖樣過於複雜或不穩定並趨向於一個穩定的機率分佈，這有助於能量更有效地找到最佳路徑。同時Damping不僅會將部分能量轉移到環境中，還可能有助於將能量更快速地集中到反應中心。這是因為耗散能夠減少能量在非理想路徑上的停留時間，促進能量沿著最佳路徑進行傳遞，從而加速整個過程。去相干和耗散效應的協同作用，使得能量傳遞的效率反而得到提升。透過量子隨機行走，科學家可以更好地理解和模擬這種複雜的量子與古典交互過程。圖三顯示了使用量子隨機行走（QSW）模擬 Fenna–Matthews–Olson（FMO）複合體在光合作用中的激子動態行為。FMO 由 7 個發色團組成，編號從 0 到 6。模擬中，我們假設激子從 5 號發色團出發，最初，激子在不同發色團之間跳躍，呈現明顯的震盪行為。然而，隨著時間推移，這種震盪逐漸減弱，系統趨向於一個穩定的機率分佈。最終，激子到達反應中心（7 號）的機率顯著提升，這一現象被稱為環境輔助量子傳輸（Environment-Assisted Quantum Transport）。
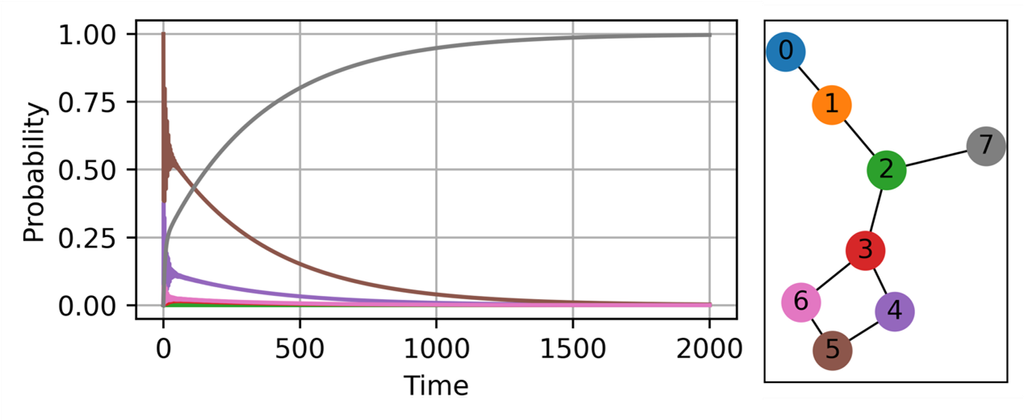
圖三: FMO複合體在光合作用中的激子處於各個發色團（編號0到6）以及反應中心（編號7）的機率。能量很快的最後都傳遞到反應中心。
量子頁面排名演演算法
量子隨機行走除了可以來分析量子開放系統外，也可以純粹當成數值工具來加速分析許多社會複雜系統的現象。例如量子頁面排名演算法（Quantum Page Rank，QPR）是一種基於量子隨機行走的網頁排名方法，是對古典頁面排名算法（Classical Page Rank，CPR）的量子版本。在古典頁面排名中，使用隨機行走的概念，模擬網頁之間的鏈接結構來評估每個網頁的重要性，並計算穩定的排名分數。相比之下，量子頁面排名利用量子疊加和干涉的特性，能夠同時探索多條路徑，從而更有效地分析網路（Network）結構的複雜性。此外，量子頁面排名還可以引入去相干和環境的影響，使其更貼近現實中動態和噪聲的網路環境。圖四比較了量子頁面排名與的排名分佈，展示了不同參數ω下的影響。從結果可以看出，在古典頁面排名（ω=1）中，影響力最高的節點主要集中在圖的兩端，而在量子頁面排名（ω=0.5,0.8）中，這些節點的排名有所下降，顯示量子行走允許資訊更均勻地傳播，減少了少數節點的支配性。此外，量子頁面排名使中間節點的排名略微上升，這與量子隨機行走的特性一致，因為量子態的相干擴散能夠加速網路中的信息流動。當權重 ω=0.8 時，排名分佈與古典頁面排名較為接近，而當 ω=0.5時，量子效應更加顯著，使排名更加均勻化，提升了部分節點的可見性。這表明量子頁面排名能夠改善網路資訊傳播的效率，避免資訊過度集中，對於推薦系統、社交網路分析等應用具有潛在價值。此外，量子特性使得量子頁面排名在某些情況下能夠更快地收斂，並且能夠更靈敏地反映網路的局部變化，為網頁排名提供另一種的分析工具。
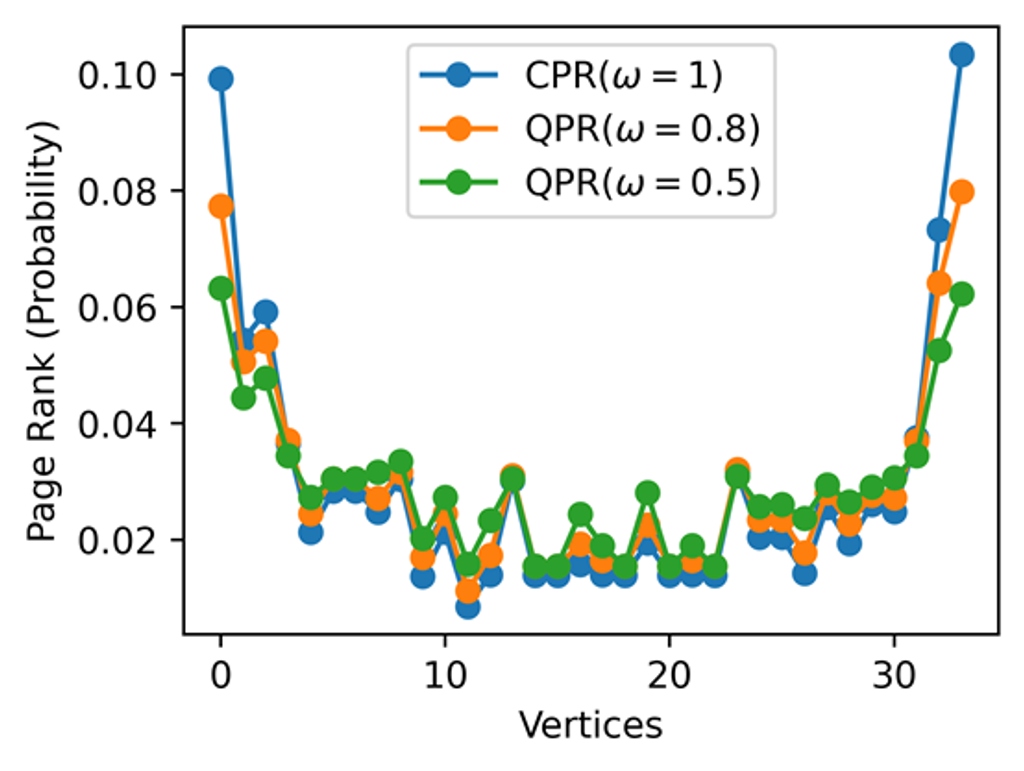圖四 古典頁面排名與量子頁面排名的比較。當ω=1時，完全為古典的行為，因此量子頁面排名演算法（QPR）等於古典頁面排名演算法（CPR）。當ω<1時，量子頁面排名演算法的量子行為會增加，並使得這些節點的排名更平均。
結語
隨著量子技術的進步，量子隨機行走有望未來在許多領域中發揮關鍵作用，例如量子計算、量子機器學習、和量子模擬。量子隨機行走可以用來設計更高效的量子算法，特別是在處理具有複雜網路結構的問題上，如社交網路分析、推薦系統、和網頁排名等。此外，量子隨機行走在理解和模擬開放量子系統的動力學方面也具有重要意義，這對於開發更穩定的量子設備和量子通訊系統至關重要。未來，隨著對環境影響或雜訊的更深入研究，量子隨機行走將在解釋和控制量子系統與環境之間的互動上提供更強大的工具，進而加速量子技術在各種領域的革新和發展。
張慶瑞教授1989年進台灣大學，曾任台大副校長並代理校長，美國物理學會(APS)與國際工程學會(IEEE)選為會士，及俄國國際工程學會(RIAE)的院士，現任中原大學量子資訊中心主任及量子電腦暨資訊科技協會理事長。
電子信箱：crchang@phys.ntu.edu.tw
王韋廷，台灣大學應用物理研究所博士生，研究領域為量子演算法，研究方向以量子行走(Quantum Walks)與量子隨機行走(Quantum Stochastic Walks)為主，並將其應用在量子機器學習(Quantum Machine Learning)。
電子信箱：d11245002@ntu.edu.tw
參考資料
[1] Whitfield, J. D., Rodríguez-Rosario, C. A., & Aspuru-Guzik, A. (2010). Quantum stochastic walks: A generalization of classical random walks and quantum walks. Physical Review A—Atomic, Molecular, and Optical Physics, 81(2), 022323.
[2] Wang, W. T., He, X. G., Kao, H. C., & Chang, C. R. (2024). Observing Majorana fermion dynamic properties on a NISQ computer. Chinese Journal of Physics, 90, 289-302.
[3] Chang, Y. J., Wang, W. T., Chen, H. Y., Liao, S. W., & Chang, C. R. (2024). A novel approach for quantum financial simulation and quantum state preparation. Quantum Machine Intelligence, 6(1), 24.
[3] Grover, L. K. (2001). From Schrödinger’s equation to the quantum search algorithm. American Journal of Physics, 69(7), 769-777.
[5] Dudhe, N., Sahoo, P. K., & Benjamin, C. (2022). Testing quantum speedups in exciton transport through a photosynthetic complex using quantum stochastic walks. Physical Chemistry Chemical Physics, 24(4), 2601-2613.
