光量子的魅力與利基
隨著人類對於微觀世界的探索，諸如原子分子的能譜、陰極射線、光電效應等的發現，開啟了對奧妙的量子現象的認識與研究。這些肇始於十九世紀中葉的新奇發現，因與當時人們習以為常的經典論述大相逕庭而備受困惑與爭論不休。直至二十世紀初，理論物理學家普朗克(Max Planck)對於古典理論無法詮釋黑體輻射( blackbody radiation)的紫外災難(ultraviolet catastrophe)問題[1]，而大膽提出所謂的量子(quanta)假說，亦即將熱輻射模式化為由共振腔體產生之振盪子(oscillators)，其輻射之模態能量($$\boldsymbol{E}_{\nu }$$)將是一與其特徵頻率($$\boldsymbol{v}$$)成正比之物理量之整數(n)倍，亦即量子能量離散化，表示為$$\boldsymbol{E}=\boldsymbol{n}\boldsymbol{h}\boldsymbol{v}$$，其中h= 6.62607×10⁻³⁴ joule∙second，即為普朗克常數；此假說成功地描述觀測到之黑體輻射頻譜，至此，量子論的成功引起了同代諸多物理學家的重視與投入探討，其中，以愛因斯坦(Albert Einstein)延伸普朗克之量子論模型，引入了光量子「光子」(“photons”，為沿用路易斯(Gilbert N. Lewis)於1926年之命名)之概念，成功地詮釋著名的光電效應(photoelectric effect)實驗，而此些開創性的量子學說之貢獻使得普朗克與愛因斯坦分別在1918年與1921年獲頒諾貝爾物理獎。量子科學的發展至此風起雲湧，繼之以波耳(Niels Bohr)之原子光譜、德布羅意(Louis de Broglie)之電子波粒二象性、海森堡(Werner Heisenberg)之測不準原理、薛丁格(Erwin Schrödinger)之量子波動方程式、狄拉克(Paul Dirac)之量子力學原理等在距今約一世紀前的劃時代研究成果，奠定了量子力學的發展基礎，更開啟了人類的「第一次量子革命」，成就了當今如半導體、雷射、核能等尖端科技，開創出如電腦、網際網路、行動通訊、先進醫療器材、低碳能源等影響人類生活型態至鉅的文明躍進里程碑。

因此可知，光的量子效應開啟了人類對量子世界的探索與認識，但這並非是歷史的偶然；相較於其他的微觀粒子，如電子、原子、離子等，光子可在多樣環境，除真空外，亦可在如空氣及諸多介質(如光纖、晶體、半導體、石墨烯等)裡傳播，因而其與介質交互作用所產生的效應(包括量子效應)能更輕易地被觀察及實驗驗證。而研究光子與各式介質交互作用所產生的各式線性與非線性的現象與機制即是所謂的光電學(photonics)，已廣泛應用在大家熟知的固態照明、太陽能電池、液晶/發光二極體顯示器、數位相機、生醫影像、光通訊、雷射加工等高科技民生產業上，這些也都是「第一次量子革命」光子技術所帶來的重大貢獻。

然而，被認為位於量子物理最核心與神奇的現象--糾纏(entanglement)，卻幾乎在「第一次量子革命」裡缺席；不是它無關緊要，而是人們對它的原理機制難以理解，遑論可以輕易地駕馭與運用它--恐怕至今都是如此！此現象發生在兩個或多個粒子所形成的一個量子體系，其個別粒子之量子態無法被明確地單獨描述，所能描述的是整體所呈現的一個疊加(superposition)量子態，類如糾結在一起的狀態，所以被薛丁格稱為量子糾纏，其奇妙之處在於此整體性與距離無關，即此量子系統裡的粒子不論距離多遠都將維持所建立的糾纏關聯性(correlation)，彼此仍相互影響著，以維持其整體性，直到因為對其進行量測，造成量子態的坍塌(collapse，因個別粒子量子態已可明確地單獨描述)，或因外在環境的影響而失去其同調關聯性，而失去其糾纏性。此非定域實在性(local realism)的反直覺現象違背了基於一般認知的因果實在論的古典物理，愛因斯坦將之稱為「鬼魅般的超距作用」("spooky action at a distance")。因此，當時以愛因斯坦為首的物理學家們認為量子力學的理論並不完備，量子糾纏等現象是在存在無法觀察到之隱變數(hidden variable)的影響下的統計結果[2]，基於支持此學說，1960年代，約翰．貝爾(John Stewart Bell)提出了著名的貝爾不等式(Bell inequalities)理論[3]，主張如果存在隱變數，則通過對糾纏粒子的大量測量結果，其之間的相關性將永遠不會超過某個值；此理論因此提供了一種以實驗方法來驗證量子糾纏存在非局域性(nonlocality)作用，並作為其與古典定域實在論之分野。自 1972 年約翰·克勞澤(John F. Clauser)團隊開始，眾多科學家以光子陸續進行量子糾纏實驗，尤其在1982年阿蘭·阿斯佩(Alain Aspect)團隊消弭了克勞澤實驗有漏洞的疑慮後， 所有實驗結果均顯示違反貝爾不等式，再加之安東．塞林格(Anton Zeilinger)團隊成功地展示了光量子遙傳(quantum teleportation)實驗[4]，至此，量子糾纏的現象在眼見為憑下開啟了量子力學應用的新頁，也因此，克勞澤、阿斯佩及塞林格於2022年共同獲頒諾貝爾物理獎，以表彰他們以光量子糾纏實驗，奠定了量子資訊科學發展的重大貢獻。

因此，不意外地，開啟了人類「第一次量子革命」的光量子，百年後再次引領人類進入了「第二次量子革命」(亦簡稱為「量子2.0」)，此次革命的引燃在於人類對於運用上述量子力學中獨特的糾纏、 疊加及不可複製(no-cloning)等現象的技術能力已跳脫所謂的思想實驗(thought experiment)層次，而達到可工程實現的階段，並在二十一世紀初；也就是當前，正如火如荼地朝實現具有強大平行處理的超高速計算、絕對安全通訊、超高靈敏度感測等量子前瞻科技邁進，此些議題如圖一所示。因為這些量子科技具有以古典方法窮其力亦無法達成的強大能力，面對此「量子優勢/霸權」(quantum advantage/supremacy)即將帶來的巨大衝擊，近年來，全球在此新興科技的研發上已掀起龐大的投資與競爭，只因此技術不只高度關乎國力與國安，其在醫藥、能源、天災、金融、環保、通訊等攸關人類生活福祉上更具革命性的影響。

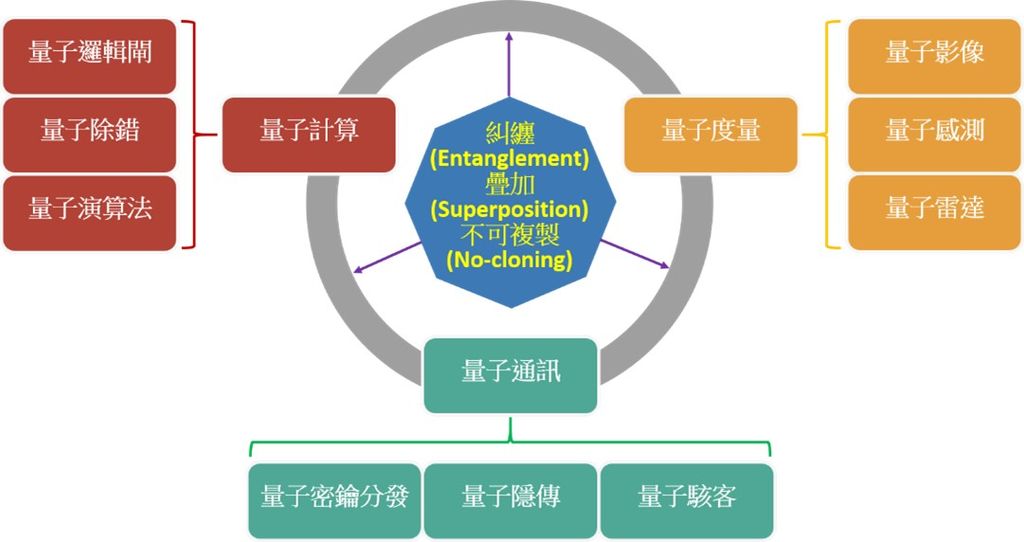
圖一 「第二次量子革命」運用量子力學中獨特的糾纏、 疊加及不可複製等現象研發具有強大平行處理的超高速計算、絕對安全通訊、超高靈敏度感測等量子前瞻科技。

 

當然，「第一次量子革命」影響人類生活最為廣大的要算是半導體(亦即電子)產業了，當今人手一支的手機便可處理日常大部分事務即是其產物。隨著大數據時代的來臨，據估計，全球產生的數位資料量正呈級數的成長(已達1021位元組等級)，然而，積體電路的擴充速度卻受限其技術的瓶頸正面臨極大的挑戰，由電子世代邁入光子時代是一種挑戰，也是人類科技演進的一個機會；相較於電子，光子具有高傳輸速率、高頻寬、高訊息密度、高調制速度及高效能等優勢，矽光子(Si photonics)技術的崛起，在於延續積體電路的發展路徑，開創積體光路(photonic integrated circuits)技術，在光電(包含矽基)晶片上建構各種處理光子訊號的元件及系統。事實上，此技術已主導了如光纖通訊、光達、低軌衛星通訊、光感測、光量子電腦等光電次世代新興科技產業，而積體光路之摩爾定律也已發表[5]。

正值人類的第四次工業革命(工業4.0)，光子正持續扮演關鍵角色，其中的積體光路正是當前實現光量子電腦的主流技術，而在量子通訊/遙傳及量子感測技術的研發上，光子更是目前唯一的有效解決方案，此次的量子革命，光子技術將再度引領前行。

本文將聚焦在如何以新興之積體光路技術邁向實現晶片級量子電腦作基礎性地介紹。此研究方向也是國科會量子科技專案計畫之重要推動項目之一。

光量子計算
在「量子2.0」之光量子技術發展上，量子光子源及(單)光子偵測器是研製量子電腦、量子通訊及量子感測等三大量子應用系統所需要的基本組構要件。以閘式(gate-based)光量子電腦的基本組構為例，在2001年，由Knill、Laflamme及Milburn (KLM)等三位學者所提出的模型，光子量子位元(photonic qubits)源、線性光學元件及(單)光子偵測器為三大硬體組件，並輔以離線量子遙傳(offline teleportation)、後選擇(postselection)等以量測為基礎的技術來達成通用型(universal)的計算能力[6]。以下我們將分別就此三大組構光量子電腦的基本元件作介紹，以一窺光量子計算之概念。

一、光子量子位元
所謂的量子光源為其特性與行為僅能以量子力學而無法以古典的理論模型來描述[7]，從而可與雷射(同調光源)或尋常古典光源(非同調光源)以量子特徵比對方式分辨出來，例如最典型也較具量子意象(粒子性)的量子光源即是單光子源，該光源理想上每次僅發射出一個光子，稱為抗成束(antibunching)光源，連續發射的單光子，彼此間之特性不可區分(indistinguishable)，其光子場統計上為亞泊松分布(sub-Poissonian distribution)。一般常見的非同調光源則發出成束(bunched)的光子，統計上為超泊松分布(super-Poissonian distribution)，而同調光源如雷射則發出隨機的光子間距(random photon spacing)，統計上則為隨機事件的泊松分布(Poissonian distribution)。單光子源其特性可以漢伯里·布朗及特維斯干涉術(Hanbury-Brown Twiss Interferometry)[8]來驗證並區分古典光源，所量得之二階關聯函數，g(2)(0)[9]，其值對於理想單光子源為0，而古典光源如雷射，即使將其輸出之平均光子數衰減至遠低於1，其g(2)(0)仍為1。此般弱雷射(weak lasers)，因其可產生較高的密鑰率，卻是目前量子密鑰分發(quantum key distribution)通訊系統裡常用的「單光子源」，雖然其安全防護性不若採用真正的單光子量子源，理想上具有絕對安全性。

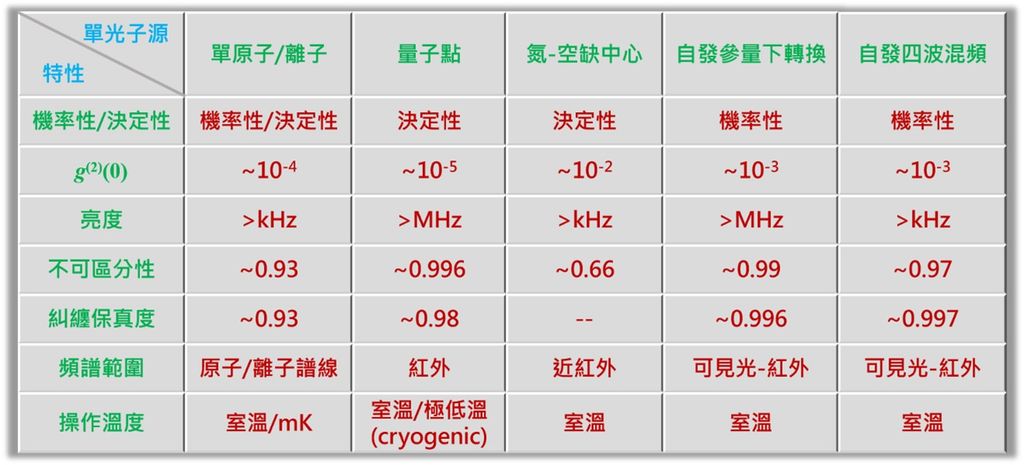
抗成束單光子源可以從單一輻射子體系(Single-emitter systems)產生[9]，如單原子/離子/分子、量子點(人造原子)、氮-空缺中心等型態介質，但此些系統受限其躍遷能階或材料能帶，可發射頻譜範圍或可調性較侷限，且多需要操作在真空或極低溫(cryogenic)環境，不利於系統的擴充性及積體性。抗成束單光子源亦可透過非線性光學材料以自發參量下轉換(spontaneous parametric downconversion; SPDC)或自發四波混頻(spontaneous four-wave mixing) 機制產生高關聯性的光子對(photon pairs) [10]來製備，該光子對，一稱為信號光(signal)，另一稱為閒置光(idler)，它們在滿足能量守恆及特定的相位匹配下同時產生，因此可具有多自由度(如時間、頻率、偏振、模態、相位等)的關聯性，除可以用來製成預示(heralded)型單光子源，以閒置光子來預示信號光子的存在，另外，根據光子對的關聯性，也可以用來製成上述各種維度的量子糾纏光源，應用性極佳。除了具粒子離散（discrete-variable；DV）特性的抗成束單光子源，上述的非線性光學參量下轉換放大(amplification)機制亦可以在光的波動特性上達成如真空壓縮態（squeezed vacuum state）來傳遞連續變量（continuous-variable；CV）的量子資訊。以參量下轉換方式產生之量子光源代表性的材料為鈮酸鋰(LiNbO3)[11]，其具有相當高的二階非線性(quadratic nonlinearity )，並透過準相位匹配(quasi-phase-matching)技術[12]來達成高效率的光子對產生(107 Hz)[13]或獲得高壓縮率之真空壓縮態(>-8 dB)[14]；而以自發四波混頻產生之量子光源代表性的材料為矽基如矽(Si)或氮化矽(Si3N4)，雖其使用到較低的光學非線性(第三階)，但其與現今半導體技術高度相容，因而具有較佳的系統整合性及低成本的優勢。離散與連續變量兩種量子光源皆已被採用來建構各式量子系統，各有其特色[15]，並分別為光量子電腦兩大代表性公司PsiQuantum及Xanadu所採用。表一整理了一些代表性的單光子源並比較它們的一些特性。相較於其他的量子資訊處理單元(量子位元(quantum bits; Qubits))平台，如超導電路、離子阱、中性原子、電子自旋等，光子量子位元(photonic qubits)可在一般環境及室溫工作、彼此不易互相干擾、無須隔絕外在電磁場的影響、可直接與光纖網路連結、高積體性（矽光子平台、鈮酸鋰光子平台）、高相容性(與矽基積體電路)、高擴展性（high scalability）等特性，是目前量子電腦技術中最可能晶片化的技術之一。

 

表一 一些代表性的單光子源及特性比較

有別於古典數位計算的基礎邏輯位元(bits)不是0就是1，邏輯量子位元(qubits)則可以處於一由0與1所疊加(superposition)的狀態，這是量子運算具有真正平行處理威力的根源。量子位元疊加態採量子力學狄拉克標記（Dirac notation），則可表示為 |ψ>=α|0>+β|1>，其中，及為機率係數（|α|^2+|β|^2=1），而|0> 和 |1>表示邏輯態 0及1(亦可是粒子數態number state或稱Fock state中分別代表真空態及單光子態)。這樣的複數希爾伯特空間(Hilbert space)向量可以在幾何空間中用一布洛赫球面（Bloch sphere）上的某一個點來更直覺地表示，如圖二(a)所示。運作上，球面上的任何一點量子位元態可以透過量子邏輯閘的各種么正操作（unitary operation）來進行可逆的量子態轉換，亦即操控量子位元在被量測時其坍塌為├ 0⟩ 或是 ├ 1⟩的機率(即|α|^2或是|β|^2)來進行邏輯運算，這樣的么正操作的計算性質是古典電腦所無法辦到的，也是通用型量子電腦的運行模式。較之其它如超導/離子/電子等的固態(solid-state)位元，光量子位元(可稱為飛行位元(flying qubits))擁有獨特的優勢，可將其雙態(|0> 和 |1>)建立在多種如前所述的自由維度上，以常見的偏振維度為例，可以以互相正交的水平|H>及垂直|V>偏振態來當基底(稱為「本徵態」)，在么正操作上，我們可以將初始偏振態為|H>或|V>的光量子位元透過線性光學元件中可以改變光子偏振狀態的光學波板(如四分之一波板、半波板，其工作原理請參考[16])組合轉置到任意一個偏振量子位元態：|ψ>=|H>+|V>，如圖二(b)所示，因此，不同的波板組合(或線性光路結構)，即是所謂的各式光學量子邏輯閘(quantum logic gates)，每一個量子邏輯閘的運作在運算上可以以一么正矩陣來代表。以一個重要的單量子位元量子邏輯閘，哈達瑪閘(Hadamard gate，簡稱H 閘)為例，它用於將量子位元由本徵態轉置為均勻疊加態，亦即，|H>→(|H>+|V>)/√2或|V>→(|H>-|V>)/√2，其么正矩陣為：

其光學操作上可以一光軸偏轉角度為22.5°之半波板來實現，如圖二(c)所示。

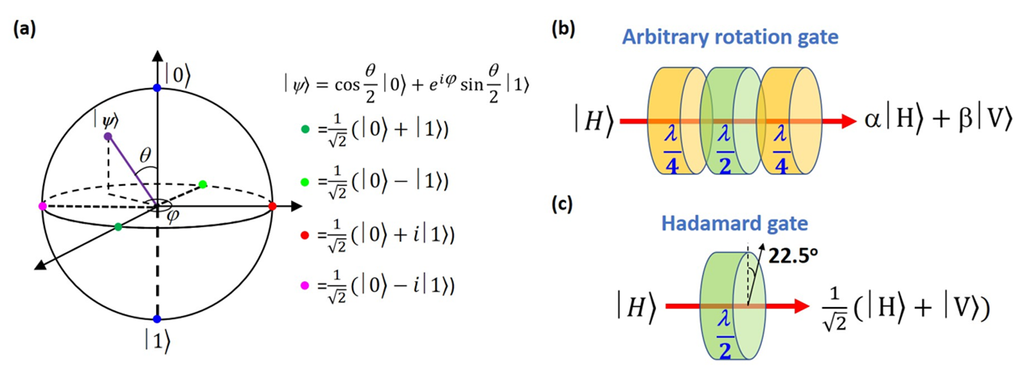
圖二 (a)以布洛赫球面(Bloch sphere)表示量子位元運作之希爾伯特向量空間(Hilbert space)。(b)在么正操作上，我們可以將初始偏振態為├ H⟩或├ V⟩的光量子位元透過光學波板(如四分之一波板、半波板)組合轉置到任意一個偏振量子位元態。(c)哈達瑪閘操作上可以一光軸偏轉角度為22.5°之半波板來實現。

二、線性光學元件
當然，隨著運算的維度加大，雙量子位元乃至多量子位元量子邏輯閘也將運用於系統中，由2n2n維度的么正矩陣來描述，其中，n為量子位元數，也因此，可以這麼說，傳統電腦要有同等的算力則需2n個古典位元數(例如，要模擬一100個量子位元的量子邏輯運算，則須使用高達2100個古典位元數！)。各式應用在量子運算的量子邏輯閘可參考文獻[17]，而世界上第一個量子邏輯閘即是以光學架構方式提出的[18]。我們這裡舉受控反閘(Controlled NOT gate，簡稱CNOT 閘)為例，它是一個雙量子位元量子邏輯閘，其中一輸入位元為控制(control)位元，當其為|0>時，另一輸入位元，稱為標的(target)位元，其輸入態不被做任何的操作而輸出，反之，若控制位元為|1>時，則標的位元之輸入態將被施以邏輯反閘(NOT)而輸出，其么正矩陣為：

CNOT閘是組成通用型量子邏輯運算線路的基本邏輯閘之一，其重要性在於任何一個多量子位元量子邏輯閘皆可用其並搭配單量子位元量子邏輯閘來組構而成。CNOT閘光學操作上可以用多個以分光比為1:2及1:1之分光器(beam splitters)來實現，如圖三(a)所示。事實上，一個通用型的量子邏輯運算線路可以僅用兩種基本光學元件(building blocks)來組構完成，即分光器及相位調變器(phase-shifters)，它們也可以以么正矩陣來代表[6]。而上述的H閘以粒子數態量子位元操作時，亦可以一1:1之分光器配合兩個相位調變器來達成[19]，因此，CNOT閘等效上可以以兩個H閘及一個受控Z閘(Controlled Z gate，簡稱CZ 閘，由3個分光比為1:2之分光器所構成)來組成如圖三(b)所示。

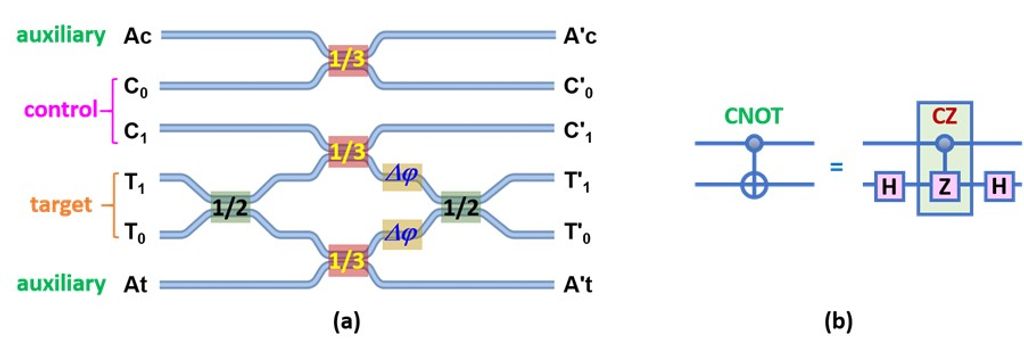圖三 (a) CNOT閘光學操作上可以用多個以分光比為1:2及1:1之分光器來實現。(b)CNOT閘等效上可以以兩個H閘及一個受控Z閘(CZ閘)來組成。

對於量子電腦的誕生所面臨的重大威脅之一即為其強大的質因數分解(factoring)的能力。RSA演算法[20]是現今包含國安、金融等資料加密所普遍採用的方法，其即是使用極大整數做因數分解的困難度來保護資訊的傳輸。據估計，即使使用現今最強大的古典超級電腦(以相當於1000個工作站等級的電腦算力為例)，對於一長度為2048位元的金鑰進行質因數分解，所需的時間將長達1012年！因此可以高枕無憂，但使用一具有量子優勢之量子位元數的量子電腦(時脈率：100 MHz)，所需的破解時間將可能不可思議地縮短至約分鐘等級[21]，屆時RSA加密法將等同失效，因而興起包括後量子密碼(post-quantum cryptography)[22]及量子金鑰分發(quantum key distribution；QKD)[23]等技術來抗衡，甚至達成絕對安全通訊的可能。此一量子電腦在大整數質因數分解效率上的明顯優勢是在1994年彼得·秀爾(Peter Shor)提出的量子演算法(Shor's algorithm)而確立的[24]，在於其可將此類龐雜的數學問題從古典方法所需的指數量級之時間複雜度(time complexity)有效降低至多項式量級之時間複雜度。技術上，秀爾演算法主要係採用量子傅立葉變換(quantum Fourier transformation (QFT))法，將質因數分解問題轉化為對模冪(modular exponential)函數之週期尋找(period finding)問題來尋解[25]。

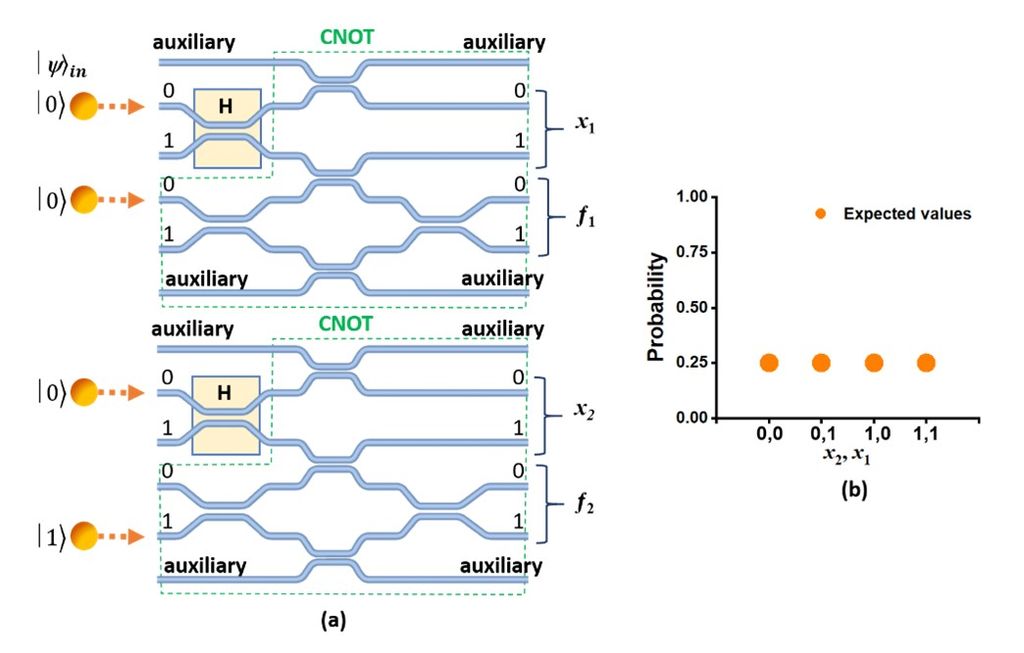
圖四 (a) 以秀爾演算法進行15之質因數分解之編匯版量子光路示意圖，主要由兩個CNOT閘及兩個H閘所組構而成。(b)於編匯版量子光路輸出端預期的結果組合有(x2,x1)=(0,0)、(0,1)、(1,0)及(1,1)，其中(0,0)為系統固有的錯誤訊號輸出，(1,0)為明顯解，代表的是因數1或15，而(0,1)及(1,1)為正解，分別代表的是因數3及5；理想的輸出機率皆為1/4。

以量子邏輯閘方式進行質因數分解可以以CNOT閘及H閘等來執行運算。因當今量子電腦仍處於所謂的「有噪聲中等規模的量子系統」(noisy intermediate-scale quantum (NISQ))時代[26]，擁有除錯能力的邏輯量子位元(logic qubits)相當有限，因此，目前以量子邏輯閘已展示的質因數分解之最大數僅至15=35，且近期主要的進展就是使用光量子位元來展示，且運用了所謂的編匯版(compiled version) 秀爾演算法來進一步減少所需的光量子位元[25]。依據秀爾演算法，執行15之質因數分解一般需要8+4共12個量子位元分別在兩個量子暫存器(registers)運作[25]，而編匯版則可精簡到僅用4個量子位元即可進行計算，簡化了量子邏輯線路及提高運算的保真度(fidelity)及可靠度。質因數分解15之編匯版秀爾演算法量子光路示意圖如圖四(a)所示[27]，主要由兩個CNOT閘及兩個H閘所組構而成，亦即基本上，可由不同分光比之分光器及相位調變器等線性光學元件(building blocks)在積體光路晶片上製作完成。在對此編匯版光路輸入(如圖四(a)箭頭所指)一預設的初始化量子態，|ψ>_in=|0>_x1 |0>_x2 |0>_f1 |1>_f2，此四量子位元將在此光路進行量子干涉，產生兩個糾纏貝爾態(entangled Bell states [28])的相乘結果：1/2(|0>_x1 |0>_f1+|1>_x1 |1>_f1)(|0>_x2 |1>_f2+|1>_x2 |0>_f2)，因此，於輸出端預期的結果組合有(x2,x1)=(0,0)、(0,1)、(1,0)及(1,1)，其中第一種為系統固有的錯誤訊號輸出，可以忽略，第三種為明顯(trivial)解，代表的是因數1或15，而第二及第四種則為正解，分別代表的是因數3及5；理想的輸出機率分布如圖四(b)所示。

隨著矽光子等積體光路晶片技術的快速發展，建構通用型可程式(programmable)重置式(reconfigurable)光量子處理器來實現大尺度高維糾纏量子光路運算器，並輔以時間、波長多工(multiplexing)等光子獨有之技術，已成了光量子電腦擴充至百萬個物理量子位元(藉此預估可達百顆以上之邏輯量子位元)，真正展示超越古典計算能力之量子優勢之可行方案之一。當今最先進(state of the art)的積體光子量子運算或資訊處理晶片為在矽基材料上整合16個光子對源、122個分光干涉儀、256個波導交合器、64個光柵耦合器及93個熱光相位調變器等非線性與線性光學元件達成一可程式可重置1515維度的量子資訊處理晶片[29]，尺寸約在公分等級。而更高維度的光量子計算機則為2020年底發表的「九章」[30]，以相當於50個單模真空壓縮態量子光源進行100100維度之么正變換(由300個分光器及75個反射鏡組成之三維干涉儀)達成76顆光子之高斯玻色採樣(Gaussian Boson sampling (GBS))，展現了其取樣速度較當時最快的傳統(超級)電腦“Fugaku”還快100兆倍，亦比2019年Google發佈的53個超導量子位元電腦“Sycamore”等效上快100億倍，徹底地展示了量子優勢。但此光量子計算機並不具有可程式性，因此，僅能就量子高斯玻色採樣此單一問題進行計算，不具通用性，此外，此系統係採用自由空間光學元件所架設而成，尺寸較龐大，約一張光學桌之大小，近年其後續之工作(如「九章3.0」)，已推進至採用全光纖網路連接之架設，在性能上及空間尺寸有所精進。

三、(單)光子偵測器
目前絕大多數的光量子電腦系統使用單光子偵測器來進行光子訊號或光子數目解析(photon number resolving)的量測，也有以平衡零差偵測器(balanced homodyne detectors)來量測壓縮態光源的特性[31]。相較於單光子偵測器，平衡零差偵測器可以使用一般的二極體光偵測器(photodiodes)，其偵測效率(在1.5µm光纖通訊波段~70%)遠較雪崩式二極體單光子偵測器(single-photon avalanche diode；SPAD)高，成本也較低，但僅應用在使用連續變量壓縮態光源的量子系統上。現今單光子偵測器主要以雪崩式二極體及超導奈米線兩種技術為主，雪崩式二極體單光子偵測器[32]係工作在高度逆向偏壓(reverse bias voltage)，高於崩潰電壓之所謂「蓋格」模式(Geiger mode)區域，此區理論上具有趨近於無限大的增益，因此得以將單顆光子之訊號放大至可響應的程度，當然，雜訊及暗電流等問題也必須克服。此外，雪崩式二極體單光子偵測器可在近室溫下工作，其材料(於光纖通訊波段，如InGaAs)也與半導體基材相對相容，有利於系統之晶片積體化，但其偵測效率在光通訊波段僅約25%左右，不利於大規模(large scale)量子運算的實現。而超導奈米線偵測器(superconducting nanowire single-photon detectors (SNSPDs))[33]，其基本原理為當光子入射極低溫(約1-4 K)下之超導奈米線(材料如NbN)而被吸收時，其能量將足以拆散數百個庫伯對(Cooper pairs，即電子對，通常要在低溫超導狀態下方容易產生)，從而在該奈米線上形成一個非超導的熱點區域，透過此超導-非超導的相變而被偵測。而超導奈米線偵測器不但偵測效率高(可達85%以上)，其在其它性能上，如暗計數率(dark count rate)、時間跳動(timing jitter)、死區時間(dead time)、響應頻寬(response bandwidth)等，皆有較佳的表現，雖然必須工作在極低溫下，且成本也比二極體單光子偵測器高上許多，但其仍是目前，尤其是量子計算應用上的主流。已有許多研究嘗試將異質的單光子偵測器與量子光路元件積體在單一晶片上[34]。

光量子計算的挑戰與最新進展
如同其它量子位元平台所面臨的挑戰類似，光量子位元要邁向實用性之通用型量子電腦的主要技術瓶頸在於建立具有容錯(fault tolerant)能力的計算系統。這基本上將與如何產生高穩健(high robust)度及具除錯(error correction)能力的光量子位元息息相關。如前所述，光量子因其不易受到外部環境的干擾，而具有相對高的穩健性，因此，建立整體運算系統所根基的材料平台與積體光路結構便幾乎決定性地影響了其性能。如同其它的科技發展路徑，材料總是扮演了該技術發展的關鍵角色；光量子技術的積體晶片化最終的挑戰將是找到共容性高的光電材料平台能將三主要硬體結構(光量子位元、線性量子運算光路及單光子偵測器)作低損耗(low loss)、高穩固性(high stability)、高擴充性(high scalability)、高保真度(high fidelity)及高積體(high integrability)之(異質)整合以實現實用性之通用型光量子電腦，概念上之積體光量子運算晶片平台如圖五所示。目前積體光量子平台以矽基材料與(薄膜)鈮酸鋰材料為主，如前所述，使用矽基平台主要著眼於其製程的高成熟度與其之高積體與高相容性，但其缺乏高速主動調制所需的光學非線性機制，多以用來建構被動式元件為主，鈮酸鋰平台特性恰多與矽基材料互補，如表二對兩大積體光量子材料平台所作的比較；鈮酸鋰材料以具有高(二階)光學非線性著稱，是先進積體光路在糾纏光子對產生、波長轉換、高速電光調制器、光開關、光學多工器等建構主動元件的重要基材。基於鈮酸鋰光路目前在製作上仍具有較高的複雜度，成本也高，因此，在建構光量子計算晶片上仍以矽基材料平台為主流，如，兩大光量子電腦公司PsiQuantum及Xanadu，皆與世界知名矽光子代工大廠合作，正朝建構百萬顆光量子位元之晶片級量子電腦目標前進。

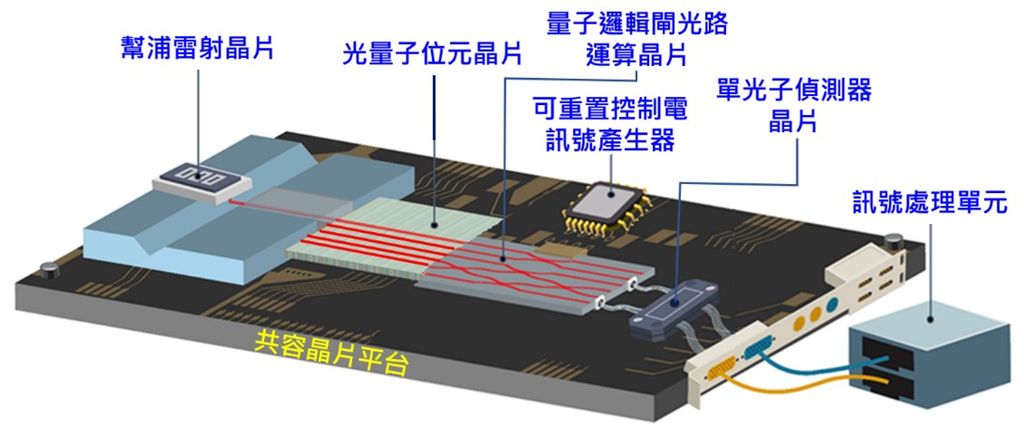
圖五 光量子技術的積體晶片化最終的挑戰將是找到共容性高的光電材料平台能將三主要硬體結構(光量子位元、線性量子運算光路及單光子偵測器)整合以實現實用性之通用型光量子電腦(概念圖)。

 

表二 矽基與薄膜鈮酸鋰材料平台之特性比較

而在發展具容錯能力的量子計算上，PsiQuantum以其獨特的多量子位元糾纏融合(Fusion-based)  技術[35]，達成其離散變量量子位元規模擴充的除錯能力，而Xanadu則利用其連續變量壓縮態量子位元之獨特特性來產製具有除錯能力之量子玻色子碼(Bosonic codes)-- Gottesman-Kitaev-Preskill (GKP)態[36]，再以光學網路連結方式進行大規模的容錯擴充[37]。

我國在國科會量子科技專案計畫之推動下，光量子電腦的研究亦為重要的推動項目之一。本團隊在國科會計畫「非高斯連續變量積體光電晶片量子計算」(以下簡稱「本計畫」)結合了我國最堅強的光量子技術研究群(來自中央大學、清華大學、淡江大學及中正大學等)，以世界領先之光量子計算技術為追求標竿(如上述之PsiQuantum及Xanadu團隊)，旨在達成建立晶片級光量子運算之先進技術研發；包括量子光源晶片(離散與連續變量量子位元)、積體光路計算晶片(展現與驗證光量子計算優勢)、單光子偵測晶片(具光子數解析能力)及晶片型光量子電腦之容錯方案開發等技術，計畫架構圖如圖六所示。

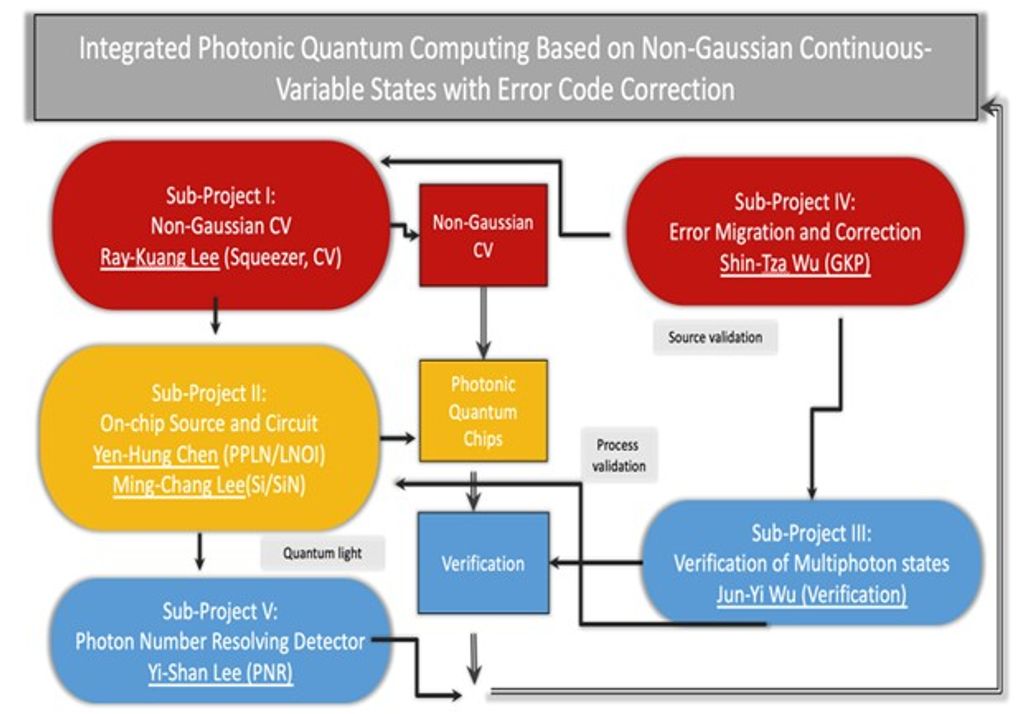
圖六 國科會計畫「非高斯連續變量積體光電晶片量子計算」之計畫架構圖，旨在達成建立晶片級光量子運算之先進技術研發；包括量子光源晶片、積體光路計算晶片、單光子偵測晶片及晶片型光量子電腦之容錯方案開發等技術。(「非高斯連續變量積體光電晶片量子計算」計畫團隊提供)

在量子光源晶片的研發上：除了以矽基材料平台外，本計畫以具更高光學非線性之基材-- (薄膜)鈮酸鋰，作為建構離散與連續變量量子位元之平台，目前已完成積體四量子位元光源晶片，為執行Shor’s algorithm運算晶片之重要量子位元、實現台灣第一個自製之即用型(turn-key)量子光子對源模組、研製出台灣第一個真空壓縮態量子光源晶片(壓縮率達-3.1 dB)、成功展示世界上第一個以預示光子對加光子方式之光學薛丁格貓態(Cat states)產生器(註：薛丁格貓態是一種非高斯量子態，可以由真空壓縮態與單光子態交互作用後產生，更可進一步實現GKP量子態的產生，是本計畫追求的目標之一)[38]、展示一高積體偏振糾纏貝爾態量子光源晶片、及完成一全自製時間-頻率糾纏量子光源，並以其透過中央大學至中華電信研究院間30 km光纖網路完成我國第一次的長距離跨區實域之量子糾纏分布(quantum entanglement distribution)實驗等。

在積體光路計算晶片的研發上：本計畫主要採以矽基材料平台來建構各式所需之光量子運算晶片，如量子邏輯閘、秀爾演算法、44 可重置線性運算光路(註：亦可操控為高斯玻色採樣光路，當以4個真空壓縮態量子光源作為輸入態時，並輔以光子數目解析偵測器，將可用來產生GKP量子態，是Xanadu公司採用的方法[37]，亦是本計畫主要的研究方法)、6×6 可重置線性運算光路(將作為多體糾纏驗證方法)等。此項研究目前已完成製造低損耗 Si₃N₄ 6x6 光學 CNOT 邏輯閘及真值表量測 (平均閘運作保真值~90%)、完成一4×4可編程積體光路的硬體架構、及完成兩光量子位元糾纏驗證系統之量測等。

在單光子偵測晶片的研發上：本計畫自製高效率具光子數解析之InGaAs/InAlAs單光子雪崩二極體偵測器，多項研究成果居於世界前沿地位，包括，成功展示具光子數解析能力之高偵測效率(>74 % at 225 K)單光子雪崩光電二極體及一高一致性4×4單光子雪崩光電二極體陣列、成功以近室溫單像素雪崩式單光子偵測器成功解析出五個光子態，超越世界紀錄、及達成以時間複用多工技術實現光子雪崩二極體偵測器之光子數解析能力等。

在晶片型光量子電腦之容錯方案的研發上：此方面研究就本計畫所規畫建構的晶片級光量子電腦硬體架構，以理論構建出包括適用於多光子多模線性光學體系的貝爾不等式的理論框架、模組化（分佈式）光量子計算的量評理論、完成以線性光學方式進行「量子漫步」達成GKP編碼之系統設計、及以線性光學裝置實現量子貓態與壓縮貓態之糾錯等重要的系統分析、診斷與容錯運算的方案建立。

圖七為本計畫執行至今之亮點成果之簡要呈現。

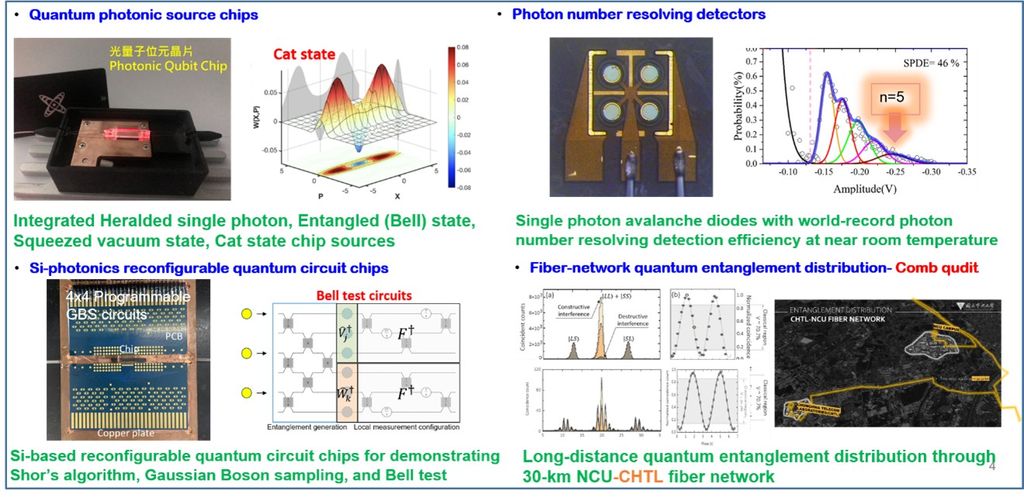
圖七 國科會計畫「非高斯連續變量積體光電晶片量子計算」執行至今之亮點成果。(「非高斯連續變量積體光電晶片量子計算」計畫團隊提供)

結語
毫無疑問地，光量子技術將再次引領人類進入更加躍進的科技文明，然如同其它的量子技術方案，以量子糾纏為發展基礎的光量子技術仍處在早期研發階段。不同的量子技術方案有其競爭性也有其互補性，光量子技術之獨特優勢在於可在一般環境、室溫下操作，以及可晶片化的潛力，另外，光量子資訊可以光速自由傳播，具有多個物理自由維度可供編碼，因此，光量子技術可同時應用至量子電腦、量子通訊及量子感測等全方位量子應用範疇。鑒於我國在光電與半導體科技產業所建立居於世界領先的基礎，國科會也已投入量子科技專案計畫建立量子國家隊，此將有利於與全球先進團隊共同合作，光量子技術的發展前景令人期待。

 

參考文獻

[1] H. Kragh, “Max Planck: the reluctant revolutionary,” Phys. World 13, 31-36 (2000).
[2] A. Einstein, B. Podolsky, and N. Rosen, “Can quantum-mechanical description of physical reality be considered complete?,” Phys. Rev. 47, 777-780 (1935).
[3] J. S. Bell, “On the Einstein Podolsky Rosen paradox,” Phys. Phys. Fiz. 1, 195 (1964).
[4] D. Bouwmeester, J. W. Pan, K. Mattle, M. Eibl, H. Weinfurter, and A. Zeilinger, “Experimental Quantum Teleportation,” Nature 390, 575-579 (1997).
[5] https://www.scienceshot.com/post/silicon-photonics-how-this-is-changing-high-speed-data-communication.
[6] E. Knill, R. Laflamme, G. J. Milburn, “A scheme for efficient quantum computation with linear optics,” Nature 409, 46-52 (2001).
[7] H. Paul, “Photon antibunching,” Rev. Mod. Phys. 54, 1061-1102 (1982).
[8] R. H. Brown and R. Q. Twiss, “Interferometry of the intensity fluctuations in light. II. An experimental test of the theory for partially coherent light,” Proc. R. Soc. A 243, 291-319 (1958).
[9] M. D. Eisaman, J. Fan, A. Migdall, S. V. Polyakov, “Invited review article: Single-photon sources and detectors,” Rev. Sci. Instrum. 82, 071101 (2011).
[10] G. Fujii, N. Namekata, M. Motoya, S. Kurimura, and S. Inoue, “Bright narrowband source of photon pairs at optical telecommunication wavelengths using a type-II periodically poled lithium niobate waveguide,” Opt. Express 15, 12769-12776 (2007).
[11] L. Arizmendi, “Photonic applications of lithium niobate crystals,” phys. stat. sol. (a) 201, 253-283 (2004).
[12] J. A. Armstrong, N. Bloembergen, J. Ducuing, and P. S. Pershan, “Interactions between light waves in a nonlinear dielectric,” Phys. Rev. 127, 1918-1939 (1962).
[13] K. Wang et al., “Quantum metasurface for multiphoton interference and state reconstruction,” Science 361, 1104-1108 (2018).
[14] T. Kashiwazaki et al., “Over-8-dB squeezed light generation by a broadband waveguide optical parametric amplifier toward fault-tolerant ultra-fast quantum computers," Appl. Phys. Lett. 122, 234003 (2023).
[15] T. Darras, B. E. Asenbeck, G. Guccione, A. Cavaillès, H. L. Jeannic, and J. Laurat, “A quantum-bit encoding converter,” Nat. Photon. 17, 165-170 (2023).
[16] E. Hecht, Optics (4th ed.), Addison-Wesley. pp. 352-5 (2001).
[17] A. Barenco et al., “Elementary gates for quantum computation,” Phys. Rev. A 52, 3457 (1995).
[18] G. J. Milburn, “Quantum optical Fredkin gate,” Phys. Rev. Lett. 62, 2124-2127 (1988).
[19] N. J. Cerf, C. Adami, and P. G. Kwiat, “Optical simulation of quantum logic,” Phys. Rev. A 57, R1477(R) (1998).
[20] R. Rivest, A. Shamir, L. Adleman, “A Method for Obtaining Digital Signatures and Public-Key Cryptosystems,” Commun. ACM 21, 120-126 (1978).
[21] R. J. Hughes, “Cryptography, quantum computation and trapped ions,” Phil. Trans. R. Soc. A. 356, 1853-1868 (1998).
[22] L. Gasser, Post-quantum Cryptography. In: V. Mulder, A. Mermoud, V. Lenders, B. Tellenbach (eds) Trends in Data Protection and Encryption Technologies. Springer, Cham (2023).
[23] C. H. Bennett and G. Brassard, “Quantum cryptography: Public key distribution and coin tossing,” Proceedings of IEEE International Conference on Computers, Systems and Signal Processing, volume 175, page 8. New York, 1984.
[24] P. W. Shor, “Algorithms for quantum computation: Discrete logarithms and factoring,” Proceedings 35th Annual Symposium on Foundations of Computer Science, 124-134 (1994).
[25] C. Y. Lu, D. E. Browne, T. Yang, and J. W. Pan, “Demonstration of a compiled version of Shor’s quantum factoring algorithm using photonic qubits,” Phys. Rev. Lett. 99, 250504 (2007).
[26] J. Preskill, “Quantum computing in the NISQ era and beyond,” Quantum 2, 79 (2018).
[27] A. Politi, J. C. F. Matthews, and J. L. O'Brien, “Shor’s quantum factoring algorithm on a photonic chip,” Science 325, 1221-1221 (2009).
[28] M. A. Nielsen and I. L. Chuang, Quantum computation and quantum information (10 ed.). Cambridge: Cambridge Univ. (2010).
[29] J. Wang et al., “Multidimensional quantum entanglement with large-scale integrated optics,” Science 360, 285-291 (2018).
[30] H. S. Zhong et al., “Quantum computational advantage using photons,” Science 370, 1460-1463 (2020).
[31] M. S. Stefszky et al., “Balanced homodyne detection of optical quantum states at audio band frequencies and below,” Classical and Quantum Gravity 29, 145015 (2012).
[32] P. Gatt, S. Johnson, T. Nichols, “Geiger-mode avalanche photodiode ladar receiver performance characteristics and detection statistics,” Appl. Opt. 48, 3261-3276 (2009).
[33] C. M. Natarajan, M. G. Tanner, R. H. Hadfield, “Superconducting nanowire single-photon detectors: Physics and applications,” Supercond. Sci. Technol. 25, 063001 (2012).
[34] M. Colangelo et al., “Molybdenum Silicide Superconducting Nanowire Single-Photon Detectors on Lithium Niobate Waveguides,” ACS Photonics 11, 356-361 (2024).
[35] S. Bartolucci et al., “Fusion-based quantum computation,” Nat. Commun. 14, 912 (2023).
[36] D. Gottesman, A. Kitaev, and J. Preskill, “Encoding a qubit in an oscillator,” Phys. Rev. A 64, 012310 (2001).
[37] J. Eli Bourassa et al., “Blueprint for a Scalable Photonic Fault-Tolerant Quantum Computer,” Quantum 5, 392 (2021).
[38] Yi-Ru Chen et al., “Generation of heralded optical cat states by photon addition,” Phys. Rev. A 110, 023703 (2024). 

 

陳彥宏博士目前擔任國立中央大學光電科學與工程學系特聘教授並兼任國立中央大學量子技術中心主任，陳博士目前同時也是中華民國光電學會的理事及會士。陳博士的研究專長為非線性光學、積體波導雷射元件、積體量子光路與元件、積體微晶片固態雷射、非線性光子晶體(準相位匹配晶體)等。

陳教授所帶領的中央大學「非線性積體雷射光學實驗室」長期致力於利用最先進的非線性光學、雷射光學、積體光學和量子光學技術，研究基於鈮酸鋰光子平台的各式多功能光電元件。研究團隊所開發的新穎積體光子元件能在一個單一晶片上執行多種光學功能(如雷射產生、糾纏光子對產生、波長轉換及調變、光放大、調制、開關、多工、頻譜窄化及操控等)，這些元件是實現高度積體的光子光路的優越和關鍵組件，可應用於光通訊、遙測、量子計算/通訊/感測、慣性感測、生物醫學、顯示技術和光學儲存等多種應用領域。