
能夠計算任何複雜問題數字的通用量子電腦(universal quantum computer)還在開發之中,不過有一種專門的類比量子計算可能將取得一些突破性成果,這要感謝中國科學技術大學(University of Science and Technology of China ,USTC)潘建偉教授(Jian-Wei Pan)研究團隊的新工作1。
潘建偉與團隊的陳宇翱(Yu-Ao Chen)、姚星灿(Xing-Can Yao)和其他成員試圖研究費米子Hubbard模型(fermionic Hubbard model,FHM)的行為,這是固體裡電子的簡化理論表示,儘管是簡化的,但它捕捉到許多強關聯多體系統的微妙物理,並被認為也許和「最偉大的多體難題」相關:銅氧化物陶瓷與相關材料的高溫超導長久以來的神祕機制。但不幸地,當這個模型被當作數學問題來處理時,除了最簡單的例子,它甚至在所有的情況都無法有數值解。
USTC研究人員將這個模型看作是一個物理問題:利用光阱,他們建立一種遵循FHM哈密頓量(Hamiltonian)的超冷原子晶格,並觀察它在調整系統參數時的表現。他們並不是這方法的發明者,有幾個研究團隊已在此耕耘多年(請參閱Physics Today,2010十月號第18頁)。2017年,哈佛大學Markus Greiner與同事們觀察到橫跨他們80個光阱組成的2D晶格的反鐵磁相關性――上與下自旋的棋盤圖樣2,造成了轟動(請參閱 Physics Today ,2017年8月號第17頁)。這是最早的明顯徵兆之一,說明FHM實驗可能接近研究人員能觀察新物理的狀態,但七年來,這個基準一直沒被超越過。
現在,新的實驗顯現大約800,000個光阱的3D反鐵磁有序性,如圖1的繪圖。這個系統夠大且夠均勻,讓研究人員能夠做出定量的測量,包括系統的臨界指數――基本物理的關鍵指標。萊斯大學的Randy Hulet表示:「這篇論文橫空出世,確實讓光晶格領域恢復了活力。」

圖1、藝術家想像的反鐵磁有序粒子,以紅色與藍色的球體表示,這裡顯示的陣列為每邊17顆粒子的方塊,但新實驗所探測的冷原子晶格大小超過每個維度的5倍1,要在如此大的系統保持條件均勻是一個主要的實驗挑戰。(圖片提供:Chen Lei)
僵局?
固體的多電子波函數極為複雜,電子不停在3維空間中運動,受到原子核(本身也在移動)的勢能面(potential-energy landscape),以及其它所有電子的長程庫倫排斥力之影響。
相比之下FHM非常簡單,其費米子粒子只佔據結晶的離散節點,而且只與相同節點上的粒子作用(通常費米子的自旋為1/2,每個節點最多容納2個粒子:一個自旋向上,一個自旋向下),粒子可跳躍到相鄰節點,但不能改變它們的自旋態。這系統只有少數幾個可調參數:同一節點上粒子的交互作用能、跳躍節點所需的能量、溫度,與每節點的平均粒子密度。
考慮這樣的簡單性,FHM能捕捉如此多的固態物理真實效應(像是反鐵磁性等),或許讓人驚訝。當同節點的交互作用是排斥的、溫度夠低、並且粒子密度接近平均每節點一個粒子的所謂”半填滿”程度,粒子就會進入每一節點正好一個粒子的狀態。儘管它們不處在同一個節點,因此不會彼此作用,但量子力學與費米–狄拉克統計的微妙作用驅使它們走向一種交替自旋的模式。
反鐵磁相也在銅氧化物及其它接近零摻雜的超導體――也就是,當材料組成不提供額外電子與電洞攜帶電荷通過其它超導層時――中觀察到,因此FHM的反鐵磁性便是個誘人的暗示,也許超導相潛伏在附近。但要做到此目標,研究人員必需將溫度降得更低,並且離開半填滿狀態,而這裡知識理解是失效的。
半填滿FHM是理論研究能夠有效處理的少數情形之一,如果離開半填滿狀態,理論學家會碰到符號問題:參與的積分主要由大的正負貢獻主導,這些貢獻幾乎(但不完全)抵銷,因此很難做正確的計算,同時,實驗人員對更低溫度的追求也停滯住了。
雙重攻擊
光阱裡的費米子原子可以合理近似成離散晶格節點上的FHM粒子,而1維、2維或3維晶格形式的等間隔光阱,亦容易從反向傳播的雷射光束對的干涉圖形產生。
但這個設定需要極度低溫,為了模擬實際材料於數十到數百K出現的物理,囚禁原子的FHM實驗必須冷卻到幾十個 nK,接近冷原子物理學家目前能達到的極限。
另一個大的限制是系統均勻度(uniformity)。一般產生的雷射束為高斯分布:它們在中心最亮,在邊緣逐漸消失,因此,以高斯光束製作的2D或3D光阱晶格,中間的阱比周圍的阱深。在一個有數十個這種光阱的實驗中,很有可能系統的不同部分處於完全不同的相上。
USTC研究人員接受了這兩種挑戰。對於後者,他們建造客製化設計的繞射光學元件,將高斯光束轉換成平頭式(flat-top)的光束,整道光的強度幾乎是均勻的。利用三對平頭式光束,他們形成每個維度近100個位點寬的均勻晶格,總共800,000個位點。
不過均勻性的好處不僅於此。在一般的FHM實驗中,研究人員先將原子氣控制在一個大的高斯阱內,接著載入至較小光阱的晶格中,這個阱的中心最深,因此該處的氣體密度最高,氣體密度的不均勻性正是晶格中熵的來源。
潘、陳、姚三人與同事們做的,是把氣體放在「盒阱(box trap) 」內:一個由光組成的中空圓柱,其柱牆把原子排開,將它們維持在內。透過讓氣體平衡到對阱體積均勻的密度,他們能更均勻許多地將氣體載入到晶格。Hulet表示,「回想起來這很顯而易見,但他們是最先意識到此事的人。」更均勻的載入會導致明顯更低的熵(至少兩倍),因此更低的溫度。
王翼棄兵
(按:王翼棄兵(King's Gambit)的理念是白方在開局時就攻擊對方的中心兵。白棋在第二步中犧牲了棋子,目的是消除黑棋的中心棋子。如果黑方試圖保住多餘的棋子,那麼白方就可以迅速發展並瞄準對敵方國王加以攻擊。)
有了大且冷跟均勻的3D晶格,研究人員處在獨特的位置觀察從未在FHM見到的現象:到反鐵磁性有序的相變。重要的是,雖然Greiner與同事們已在他們的2D實驗中看到反鐵磁相關性,但他們並沒有看到實際的反鐵磁相,這個相甚至不存在於2維。相反的,反鐵磁相關性一開始很小,逐漸在更低的溫度散布到整個2維系統,當Greiner與團隊看到他們80個位點晶格橫佈著棋盤圖案,這是因為模型的相關長度已經發展到超過他們觀察的系統。
另一方面,Greiner與同事們利用量子氣顯微鏡來直接觀看棋盤圖案,但USTC研究人員並沒有這樣的選項,他們以布拉格散射代之測量他們3D晶格的自旋排列,類似利用x光散射探測真實晶體原子排列的原理。
圖2顯示他們其中一個研究反鐵磁相變的實驗。a圖是以熵(與溫度相關)與粒子密度(n)表示的系統相圖之略圖。反鐵磁相在半填滿態n=1的兩側形成對稱的圓頂,一連串藍點表示研究人員如何調整n來探測切過反鐵磁圓頂的相空間切片。
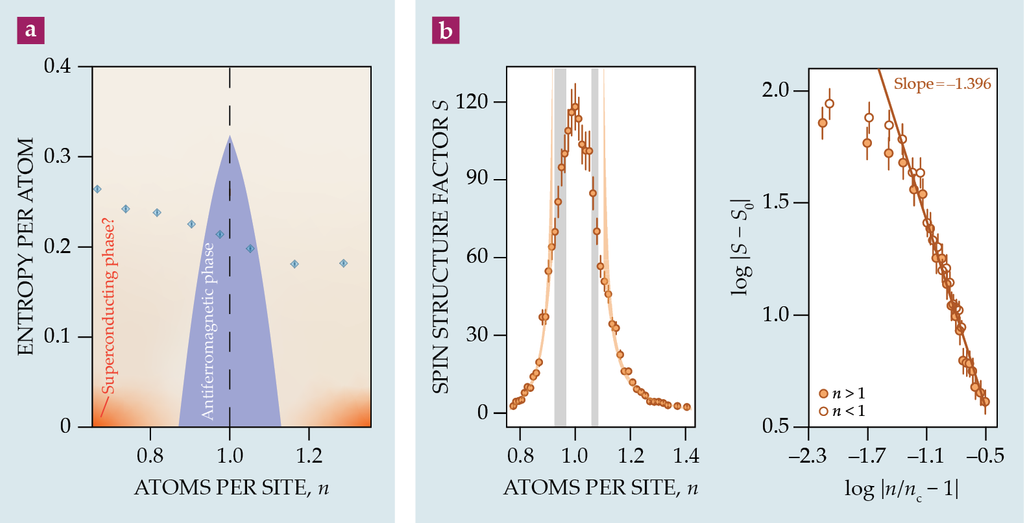
圖2、探索3D費米子Hubbard模型的相圖。(a)藍點顯示研究人員能達到的每原子熵值對原子密度n的關係,這實驗能探測進入或離開反鐵磁相的相變,但要達到假設存在的超導相,需要更進一步冷卻系統。(b)接近n=1時,自旋結構因子(spin structure factor) 有大的S,在反鐵磁相(其邊界 nc預估位於灰色帶中的某處)以外,S依著指數率依賴性(power-law dependence)衰減,如右側的對數–對數圖中顯示,指數率標度與預期的臨界指數1.396一致。(改編自參考文獻1)
圖b顯示USTC研究人員對自旋結構因子(spin structure factor)S的測量,此因子定量自旋的有序程度。如反鐵磁相的預期,S在n=1的附近為大,但在相的邊界(研究人員預估位於灰帶中的某處)以外,S並不是突然降到0,而是依著冪律依賴性逐漸減小(power-law dependence)。
冪律是由臨界指數來定義,而指數能取的值只有幾個。各種看似不同的物理系統可歸類成少數幾個普遍性類別(universality classes),每一個類別都有自己的特徵標度行為(請參閱Physics Today,2023年7月號第14頁)。FHM被認為與3D海森堡模型同屬一個普遍性類別,賦予其臨界指數1.396,但這一點從未被證實,因為FHM相變在之前未曾被觀測到。
當研究人員畫上一條斜率為−1.396的直線時,他們發現這條線與圖2b中對數–對數圖的數據相當吻合,然而,重要的是,這個實驗並不構成對臨界指數的測量。姚星灿解釋:「要準確測定冪率函數的臨界指數,需進行好幾個數量級的測量,在我們現行的工作中,並不滿足這個條件,但在未來,我們希望能精確測定這個數值。」
下一步?
潘、陳、姚與團隊已經進行了迄今最為定量、訊息量最多的FHM實驗,但還有許多工作要完成。超導相假使存在的話,所在溫度甚至低於研究人員所及的溫度,他們需要進一步的實驗改良來達到它。
如果研究人員真的做到超導相,下一步將是進行詳細的實驗,試圖揭開費米子結合成玻色子對而凝結成超流體的機制。銅氧化物超導性之所以如此神秘,部分原因在於沒有辦法去單獨調整個別的性質,舉例來說,僅是為了改變電荷載子密度,就必須製做不同化學成分的新樣品,這同時也改變了其它性質。
另一方面,在FHM,改變粒子密度就跟用更多或更少原子重新載入晶格一樣簡單。其它參數也可被調整,包括那些能使模型超越古典FHM,來模擬聲子或自旋漲落等效應的參數。透過測試每一個參數對超導性的貢獻,研究人員最終能夠揭開電子成對機制的神秘面紗。
不過理解超導性並不是是唯一目標。強關聯電子系統產生許多其它的物理現象,有一些出現在研究人員可及溫度下的FHM,「由於數值計算的困難,目前人們對低溫及離開半填滿狀態的3D FHM所知甚少,」姚星灿說道,「繪製它的相圖本身是非常重要的。」
而USTC團隊將不是唯一致力於FHM的團隊,盒阱――降低量子氣體的熵與溫度之關鍵――是個已成熟的技術,因此它對製造低熵氣體的重要性現在已為人所知,其他研究團隊也可開始應用它。產生平頭式光束的繞射光學元件是客製化設計的,不過類似的產品在市場上可以取得。Hulet表示,「其他研究團隊絕對有可能重現這些結果,潘的團隊領先所有人,但也只有早幾個月。」
參考文獻
1.H.-J. Shao et al., Nature 632, 267 (2024). https://doi.org/10.1038/s41586-024-07689-2Google ScholarCrossref OpenURL PubMed
2.A. Mazurenko et al., Nature 545, 462 (2017). https://doi.org/10.1038/nature22362Google ScholarCrossref OpenURL PubMed
3.B. G. Levi, Phys. Today 63(10), 18 (2010). https://doi.org/10.1063/1.3502540Google ScholarCrossref OpenURL
4.J. L. Miller, Phys. Today 70(8), 17 (2017). https://doi.org/10.1063/PT.3.3649Google ScholarCrossref OpenURL
5.J. Miller, Phys. Today 76(7), 14 (2023). https://doi.org/10.1063/PT.3.5265Google ScholarCrossref OpenURL
本文感謝Physics Today (American Institute of Physics) 同意物理雙月刊進行中文翻譯並授權刊登。原文刊登並收錄於Physics Today, Sep. 2024雜誌內 (Physics Today 77 (9), 12–14 (2024); https://doi.org/10.1063/pt.hjlp.dlbi )。原文作者:Johanna L. Miller。中文編譯:張鳳吟,國立陽明交通大學物理學系博士。
Physics Bimonthly (The Physics Society of Taiwan) appreciates Physics Today (American Institute of Physics) authorizing Physics Bimonthly to translate and reprint in Mandarin. The article is contributed by and was published in (Physics Today 77 (9), 12–14 (2024); https://doi.org/10.1063/pt.hjlp.dlbi ). The article in Mandarin is translated and edited by F. Y, Chang, National Yang Ming Chiao Tung University.

