前言：「近藤效應」的原始概念起源於一普通金屬中若含有一個自旋1/2的磁性雜質時，導電電子的自旋將試圖以相反方向去屏蔽這個雜質磁矩，從而在極低溫時形成一個自旋單重(基)態。引伸而言，如果金屬中含有一個具有內稟雙重能量簡併態的非磁性缺陷，在適當但嚴苛的參數平衡下，這個「量子雜質」也可能與導電電子耦合而產生「軌道(單／多通道)近藤效應」。這是量子力學不懈解答金屬導帶與(贋)自旋交互作用的一個延續近百年的重大，且極具啟發性的多體作用及基態問題。

 

磁性近藤效應

金屬的一個重要特徵是它的電阻率 ($\rho$) 隨溫度 ($T$) 下降而減小：從數百 $K$ 以下，電子—聲子散射率因溫度降低而趨緩，因此電阻率逐漸減小。由於真實的金屬樣品中都含有缺陷、雜質或界面(以下簡稱雜質)，造成在低溫時電子和雜質的彈性散射率大於非彈性電子—聲子散射率，因此電阻率趨於一個常數，不再隨溫度持續下降而改變，稱為「殘餘電阻率」($\rho_0$)，如圖1及圖2右上插圖所示——圖中的二氧化銥(IrO$_2$)和以下將討論的二氧化釕(RuO$_2$)，兩者雖是氧化物，卻都具有金屬導電性質[1]。以上僅考慮非磁性的缺陷，即雜質不帶有局域磁矩 (local magnetic moments)，因此在散射過程中不牽涉、也不需考慮導電電子自旋和雜質磁矩交互作用的問題。當缺陷為磁性雜質時，導電電子可能會與雜質產生散射、耦合或相互作用。在這一過程中，局域磁矩的方向與導電電子的自旋方向都會發生翻轉，尤其導電電子的自旋會試圖屏蔽局域磁矩，導致其自旋方向與局域磁矩的自旋方向相反，這種現象稱作近藤效應 (Kondo effect)[2–4]。當局域磁矩的自旋大小為 $S = \frac{1}{2}$ 時，隨著溫度接近絕對零度 ($T \to 0$)，局域磁矩最終會與周圍的導電電子形成一個自旋單重態 (spin-singlet) 的多體強關聯結構，這一結構被稱為「近藤雲團 (Kondo cloud)」。近藤效應的具體實驗展現為，在低溫時，樣品電阻率不再是一個常數 (即上述一般金屬中的殘餘電阻率)，而是隨著溫度下降而呈對數函數形式 (些微) 上升，直到很低溫時才會 (以 $\rho \propto T^2$ 形式) 趨於一個飽和值，並最終達到一個費米液基態。這一種低溫時上升的電阻率稱為「近藤電阻率」($\rho_K$)，可寫為 $\rho_K(T) = \rho(T) - \rho_0$。

圖1  三根二氧化銥奈米線的電阻率對溫度的變化關係。電阻率隨溫度下降而下降，總體呈金屬特性，紅色實線為波茲曼傳輸理論預測值。約在20 K以下，軌道二通道近藤效應造成電阻率隨溫度下降而些微上升，如插圖所示。

 

軌道多通道近藤效應

這種由局域磁矩造成的磁性近藤效應，是凝聚態物理學家耳熟能詳的一個重要多體物理現象／範例，其最簡單的理論描述，乃基於考慮一個自旋 $1/2$ 的局域磁矩與金屬導帶中的一群導電電子之間的 $s$–$d$ 交互作用（設想導電電子來自於金屬原子的 $s$ 電子，局域磁矩來自於磁性雜質的 $d$ 電子）。在討論近藤效應時，術語上我們將這一群為數眾多的導電電子稱為一個費米海(Fermi sea)，或一個屏蔽通道(screening channel，以下簡稱通道)，因此以上所述的最常見的近藤效應可精確稱作磁性「單通道近藤效應」(one-channel Kondo effect，簡稱1CK效應)。而許多師生比較不熟悉的是，如果雜質是一個非磁性的「量子雜質(quantum impurities)」，也就是一個內稟雙重簡併態(doubly degenerate states)，含有內在自由度(internal degrees of freedom)的雜質，則當處於適當(但嚴苛！)的條件下，也可能產生(非磁性)近藤效應[5,6]。「量子雜質」可能造成非磁性近藤效應的理論概念，是Jun Kondo於1976年首先構想和預測的。更進一步而言，理論學家又考慮了多於一個費米海／通道時的新穎情況，他們設想如果有兩個、甚至更多個費米海／通道的導電電子同時存在，並且它們都互相競爭，想去與一個內稟雙重簡併態的「量子雜質」散射時，將會發生何種新奇或不可思議的強關聯耦合現象？這個問題稱為「多通道近藤效應(multi-channel Kondo effect)」[7]，它的最簡單情況為只包含兩群導電電子／費米海和一個「量子雜質」的作用，稱作「雙(二)通道近藤效應(two-channel Kondo effect，簡稱2CK效應)」。所以理論上而言，我們可以預想磁性單／雙(多)通道近藤效應，和非磁性單／雙(多)通道近藤效應等多種問題和可能性[8]。

軌道雙通道近藤效應：二氧化銥

圖2 三根二氧化銥奈米線的低溫電阻率對溫度的變化關係。在約 $0.5$ 至 $20\ \mathrm{K}$ 間，電阻率呈 $\sqrt{T}$ 形式上升，並且不受外加磁場影響（左下角不同符號顯示有無外加垂直磁場）。通過樣品的直線為與 2CK 理論預測的擬合，從其斜率可計算出樣品中的氧缺陷含量。左上插圖顯示奈米線和次微米電極的掃描電子顯微鏡（SEM）影像，下方白色橫槓長度為 $1\ \mu\mathrm{m}$。右上插圖顯示含氧缺陷的二氧化銥奈米線（NW A）出現 2CK 效應造成的低溫電阻率上升現象，不含氧缺陷的奈米線（NW 3）則無近藤效應，出現殘餘電阻率行為。（取自文獻[9]）

 

圖二畫出三根多晶二氧化銥奈米線在零磁場和外加垂直磁場中的低溫電阻率隨溫度變化的情形[9]。圖中明確顯示約在 $25\ \mathrm{K}$ 以下，電子—聲子散射率已極微弱，而在約 $0.5$ 至 $20\ \mathrm{K}$ 溫區，電阻率隨溫度下降出現 $\sqrt{T}$ 形式上升情形；而且，電阻率的上升不受外加磁場的影響，表示樣品中不含絲毫磁性雜質。這三根奈米線的直徑為130 (NW A)、190 (NW B1)、190 (NW B2) nm，都大於彈性平均自由程，因此屬於三維波茲曼傳輸範圍。20 K以下的電阻率上升行為，則來自非磁性軌道雙通道近藤效應(nonmagnetic orbital 2CK effect)」，而非樣品的維度效應，解釋如下。(從實驗角度而言，與形狀通常不規則的小塊單晶樣品相比，奈米線樣品的幾何形狀有利於使用電子束微影技術製作次微米電極，從而對電阻率進行高解析四點量測，獲得精確數據。)

圖3  (a)金紅石晶體結構，紅色小圓球代表氧原子，灰色小圓球代表銥或釕原子，V_O1代表氧缺陷／空隙。(b) VO1與它周圍的三個銥或釕離子M1、M2及M3形成一個等腰三角形。(c) M2銥離子與它周圍的四個氧離子形成一個近乎、但不完美的四方形。(d) M2銥離子的雙重簡併5d_xz和5d_yz原子軌道示意圖。(取自文獻[9])

 

二氧化銥的晶體結構為金紅石結構(rutile crystal structure)，如圖3(a)所示。同時，二氧化銥是一種非磁性／順磁性材料。在這種晶體結構中，當化學計量組成時，一個銥原子供應四個外層電子以與兩個氧原子鍵結，此時銥離子(Ir⁺⁴)的5d原子軌道為半填滿。但是如果晶體中出現了一個氧缺陷(少了一顆氧原子)，則會「多出」兩個本應與氧離子(O^-2)形成鍵結的電子，這兩個多出的電子，我們稱之為「缺陷電子(defect electrons)」，必須「還給」氧缺陷／空隙周圍的兩個銥離子[9]。在金紅石結構中，因為氧原子與其緊鄰的三個銥原子構成一個等腰三角形(圖3(b))，所以為了降低庫倫排斥位能，兩個「缺陷電子」之中的一個會還給較遠處的M3銥離子，另外一個「缺陷電子」則還給了M1或M2銥離子(這兩個銥離子在金紅石結構中等價)。由於M2離子(或M1離子)周圍有四個氧原子，形成了一個近乎、但並不完美的四方形(圖3(c))，因此由圖3(d)可以看到銥離子的5d_xz和5d_yz原子軌道，在出現氧缺陷時對z軸具有相當穩固的四重旋轉對稱性(C_4V點群對稱，即每旋轉90度看起來都一樣)，所以能量相等。換句話說，這一個由氧空隙還回來的「缺陷電子」具有雙重簡併特性，它能填在5d_xz或5d_yz原子軌道之中的任一個，因此這個「缺陷電子」就是一種「量子雜質」，它具有內在自由度，能在適當條件下被導電電子散射，即與費米海耦合，因而從一個原子軌道跳躍（穿隧）到另一個原子軌道，產生近藤效應。這裡，樣品中不存在局域磁矩，散射過程不牽涉導電電子自旋的角色，因此是一種非磁性軌道近藤效應。（以上是初步解釋，半填滿電子在二氧化銥中佔據哪些銥離子5d原子軌道，以及雙重簡並能級之間有無庫侖作用和相互作用將造成何種效應等，都需進一步更具體定量計算。）

但是，軌道近藤效應物理的精妙和細微之處遠不僅於此。因為如上所述，整個二氧化銥樣品中不含局域磁矩，因此我們可以把導帶中的導電電子視作等價而獨立的兩群導電電子，一群自旋向上，一群自旋向下——這兩群導電電子的自旋方向長時間維持不變，因為系統中沒有能導致自旋翻轉的交互作用。所以，我們有兩個費米海，或兩個通道，它們等價又獨立不相干。這兩群導電電子都要去與M2離子上的「缺陷電子」耦合／散射，使得該「缺陷電子」在5d_xz和5d_yz兩個能量簡併的原子軌道之間跳動，這顯然便是一種軌道2CK效應[9]。更有甚者，因為這兩個等價又獨立的費米海／通道彼此競爭，導致了過度屏蔽(over-screening)現象，因此理論預測在$T \to 0$
時，系統將處於一種非費米液(non-Fermi liquid)基態。具體而言，理論預測這種非磁性軌道2CK效應將在溫度小於一個特徵溫度(稱為「近藤溫度」TK)時，產生電阻率與 $\sqrt{T}$ 成正比的行為 [10]，並且不受磁場影響，正如圖2所測量到的。軌道近藤效應不受外加磁場影響的原因，可解釋如下：由於外加數 $T$ 大小的磁場造成的 Zeeman 能量（$g\mu_B B \sim 1\ \mathrm{meV}$，其中 $g$ 為 Lande $g$ 因子，$\mu_B$ 為波耳磁子，$B$ 為磁場）遠小於一般金屬中的費米能量（$E_F \sim 10\ \mathrm{eV}$），無法使自旋向上和自旋向下的兩群導電電子在能譜上產生明顯的相對上下位移，因此兩個通道的電子數幾乎維持相等，（實驗室中合理大小的）外加磁場也就無法改變軌道近藤效應。反之，外加數 $T$ 磁場造成的 Zeeman 能量能輕易達到「近藤能量」（$k_B T_K$，其中 $k_B$ 為波茲曼常數）的數量級，因此磁性近藤效應易被外加磁場所壓制或破壞。（外加磁場對自旋 $1/2$ 磁性近藤效應造成的顯著影響，請參考 [9] 中圖3(c) 及 [11]。）

磁性多通道近藤效應的理論概念早在1980年就已經被法國物理學家Ph. Nozières和A. Blandin提出來了[7]；稍後，軌道2CK效應的理論預測也被匈牙利科學家A. Zawadowski 及其合作者[6]提出，但是40多年來，確切的實驗證據極為缺乏，文獻中關於2CK效應的報導也總是伴隨著爭議[12-14]。理由在於理論預測中嚴苛要求的兩(多)個穩定而彼此獨立並且完全等價的通道／費米海，很難在真實固體或量子材料中落實，科學家也不知該往何處去尋找 。

 

軌道單通道近藤效應：二氧化釕

為了進一步驗證圖2中的電阻率上升現象確實是由軌道2CK效應造成的，我們同時測量了五根金屬性二氧化釕(RuO₂)奈米線的低溫電阻率[9]，如圖4所示。二氧化釕與二氧化銥一樣，同樣具有金紅石晶體結構，因此它的4d_xz和4d_yz原子軌道也構成雙重簡併態，在有氧缺陷／空隙時，能產生非磁性軌道近藤效應。圖4中的 $y$ 軸畫的是歸一化的近藤電阻率（$\langle \rho_K \rangle / \rho_{K0}$），其中 $\langle \rho_K \rangle$ 為溫度 $T$ 時的平均近藤電阻率，$\rho_{K0}$ 為 $T \to 0$ 時的近藤電阻率，$x$ 軸畫的是歸一化的近藤溫度（$T / T_K$）；因為二氧化釕奈米線在低溫時常出現顯著的隨時間變普適電導漲落（temporal universal conductance fluctuations）現象，故我們取時間平均值 $\langle \rho_K \rangle$ 以減小測量誤差。圖中顯示五組歸一化的電阻率數據緊密重疊，並在三個數量級的寬廣溫度區間（$T / T_K \approx 0.03$–$3$），密切遵循如紅色實線所畫的單通道近藤標度形式(1CK scaling form)。與二氧化銥對照，前者出現軌道2CK效應，而這裡出現軌道1CK效應，原因在於二氧化釕是一種(弱)反鐵磁性材料 ，缺乏時間反演對稱性，自旋向上和向下兩群導電電子的簡併性被破壞掉了，系統因此恢復單通道行為。圖4的測量結果，驗證了圖3模型的可靠性和有效性。此外，一如圖2，圖4中的電阻率上升行為也不受外加磁場影響，請參考[9]。(圖4中的1CK標度曲線是由數值重整群論(numerical renormalization group, NRG)方法計算得到的[15]，數值解之外，1CK近藤電阻率的溫度變化行為迄今仍缺乏一個解析解，這應是近藤效應被發現近百年的一項巨大理論挑戰。)

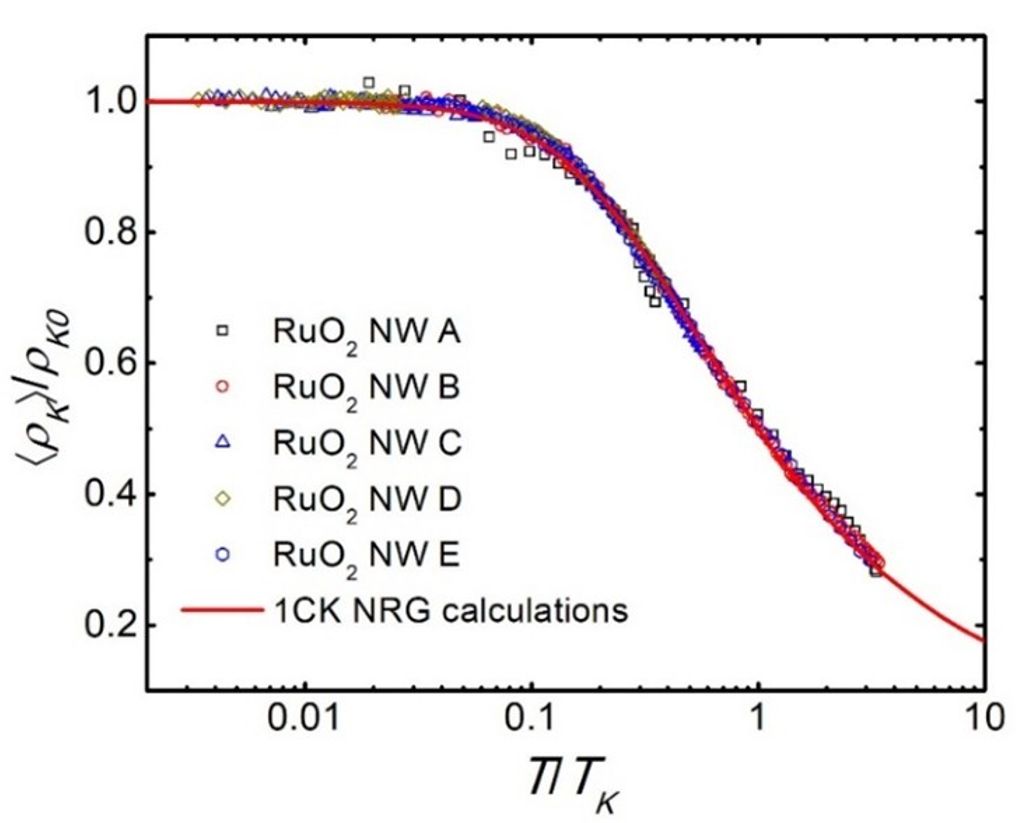
圖4  五根二氧化釕奈米線的歸一化軌道近藤效應電阻率對歸一化溫度的變化關係。奈米線的TK值分別為3.0 (NW A), 12 (NW B), 69 (NW C), 80 (NW D)和7.0 (NW E) K。五組數據緊密重疊，並與1CK標度函數形式(紅色曲線)在寬達三個數量級的歸一化實驗溫度範圍內高度吻合！(取自文獻[9])

量子材料 vs 量子點元件
最近的理論和實驗研究發現，二氧化銥和二氧化釕都是狄拉克節線(Dirac nodal line)金屬[16]，這種拓樸能帶結構屬性與軌道2CK效應的形成和穩定似乎相輔相成，都源於金紅石結構的特殊對稱性，包括鏡面反射對稱性、反轉對稱性，尤其四重旋轉(C_4V)對稱性，以及強自旋—軌道作用[9]。理論又指出，2CK 效應的低溫非費米液傳輸行為（$\rho_K \propto \sqrt{T}$），可能反映了馬約拉納零模的出現蹤跡 [17]。一些凝聚態物理學家還主張，2CK 效應可能是造成奇異金屬（strange metal）現象的原因，而量子材料中（在超導臨界溫度 $T_c$ 以上的）的奇異金屬行為常與（在 $T_c$ 以下的）非常規超導性質緊密相扣 [8]。實驗方面，圖2應是目前文獻中對真實固體中的軌道2CK效應的最確切且又(與圖4)自洽的一組實驗證據。天然量子材料之外，隨著奈米科技的進步與多年理論上及實驗上的雙重並肩努力，2CK效應曾在精心設計和嚴苛調控條件下的半導體量子點元件中，在極低溫下(< 100 mK)被觀測到[18,19]。就多通道近藤效應研究而言，量子點元件的優點在於各項實驗參數相對容易設計和掌控，缺點則在於實務上同時調控數個電極的偏壓困難度很高，元件TK值又極低，因此只能在很狹窄的溫度和能量(如偏壓)範圍內去驗證理論的預測，而且其實驗結果也無法被直接推展應用於瞭解固體材料中的電子強關聯現象。

自旋—軌道作用
自旋—軌道作用(spin-orbit interaction，簡稱SOI)是一種量子力學現象，起因於在原子核周圍運動的電子，感受到了原子核繞著它（電子自身的靜止座標）運動而產生的磁場，是一種相對論效應。SOI很強時，會改變原子能級，造成精細分裂及（部分）破壞簡併。在固體材料中，強SOI會改變能帶結構，造成自旋相關的能帶分裂(spin-split bands)，並改變高晶格對稱點附近的能譜色散(energy dispersion)關係。這一特性在拓樸材料（如拓樸絕緣體及自旋電子元件）中尤其顯著，它既起到保護表面態的作用，又有利於不受無序及外加微擾影響的邊緣態的出現，因此強SOI是孕育新穎量子相變（如量子自旋霍爾效應及拓樸超導體）的關鍵要素。

在二氧化銥中，我們可以分開討論SOI對局域在銥離子中的電子的影響，和對巡遊於整個固體中的導電電子的影響。前者，由於銥的原子序(Z = 77）很大，SOI很強，因此它的5d能級的精細分裂與簡併性質受到SOI的明顯影響。但是如前面所述，在金紅石結構中的氧缺陷周圍的銥離子具有(近似) C_4v點群對稱性，因此確保了產生軌道2CK效應所需的5d_xz和5d_yz原子軌道的簡併性。

SOI的一個重要特徵是，當對一個電子波函數取複數共軛並同時讓動量與角動量／自旋變量取負號時，該波函數與原波函數相同（不變性／不變量）。這種性質——稱為「時間反演對稱性」——保護了電子波函數的某些特徵，即Kramer簡併：每一個導電電子波函數（態）都有另一個與之對應且為正交的時間反演波函數（態），它們的能量相等（雙重簡併）。在「非磁性」二氧化銥晶體中，Kramer簡併確保了在SOI作用下的導電電子，仍具備產生軌道2CK效應所需的雙通道對稱性。最後，或許我們可以思考，如何進一步藉由精細氧缺陷工程手段(oxygen vacancy engineering) ，結合拓樸與強關聯雙重特性，製作出具備非費米液行為的「拓樸雙通道近藤系統(topological two-channel Kondo systems)」[9]。

三維電子—電子相互作用
近藤效應考慮的是一個弱無序金屬中的導電行為，但是除了近藤效應之外，弱無序金屬中的電子—電子相互作用效應(electron-electron interaction effect，簡稱EEI效應)和弱局域效應(weak-localization effect)，也會造成低溫電阻率的些微上升，或稱電阻極小值現象(resistance minimum) [20]。尤其在三維金屬中，EEI效應造成的電阻率同樣是隨溫度下降而呈√T形式上升[21]，與軌道2CK效應造成的溫度變化形式相同，這也是報導軌道2CK效應的實驗文獻常常引起爭議的主要原因所在[8,14]。在我們的二氧化銥奈米線實驗中（圖2），測得的電阻率上升量比三維 EEI 效應理論預測的上升量大了約一個數量級，而且在約 $0.5\ \mathrm{K}$ 時偏離了 $\sqrt{T}$ 行為，因此可以排除 EEI 效應 [9]。（$0.5\ \mathrm{K}$ 以下電阻率偏離 $\sqrt{T}$ 行為的原因，在於圖3(c)中的四方形稍有變形，並非完美四方形，因此 $C_{4v}$ 對稱性稍有破缺，使得 $5d_{xz}$ 和 $5d_{yz}$ 兩個原子軌道不完美簡併，有一微小能量差所致。）最後指出，因為 EEI 效應、弱局域效應和近藤效應三者都是對波茲曼傳輸行為的微擾修正，因此它們所造成的低溫電阻率上升量都遠小於樣品的殘餘電阻率大小，即（以近藤效應為例）$\rho_K / \rho_0 \ll 1$。

結語
近藤效應的物理內涵極其豐富，乃至複雜和精細。為了避免篇幅過於冗長，本文僅概略介紹磁性和非磁性、以及單通道和雙通道近藤效應概念，尤其是軌道雙(單)通道近藤效應在二氧化銥(二氧化釕)中的體現及實驗驗證，更定量的分析和討論請參考[9]。關於各種版本的(磁性、軌道、電荷等)近藤效應和電子—電子相互作用效應的原始文獻，請參考[8]和[9]中所列。除了發現二氧化銥和二氧化釕（及二氧化鋨）為狄拉克節線金屬之外，最近的一些研究指出二氧化釕可能是[22](或不是[23])一種交變（交錯）磁性(altermagnetic)材料，而且在應力下二氧化釕薄膜有超導性[24]，在在改寫了傳統認知[1]，值得追蹤關注。

 

致謝：本文中討論的實驗主要由陽明交通大學葉勝玄助理教授完成，數據由Stefan Kirchner教授進行模型建構和理論解釋。感謝陽明交通大學朱仲夏教授、中央大學楊仲準教授、天津大學李志青教授和輔仁大學吳至原副教授仔細閱讀文稿並提供修正意見。

參考文獻：
[1] J. J. Lin et al., Journal of Physics: Condensed Matter 16, 8035 (2004).
[2] L. Kouwenhoven and L. Glaszman, Physics World 14, 33 (2001).
[3] W. de Haas et al., Physica 1, 1115 (1934).
[4] J. Kondo, Progress of Theoretical Physics 32, 37 (1964).
[5] J. Kondo, Physica 84B, 40 (1976); ibid. 84B, 207 (1976).
[6] D. L. Cox and A. Zawadowski, Advances in Physics 47, 599 (1998).
[7] Ph. Nozières and A. Blandin, Journal de Physique 41, 193 (1980).
[8] S. Kirchner, Advanced Quantum Technologies 3, 1900128 (2020).
[9] S. S. Yeh et al., Nature Communications 11, 4749 (2020). 
[10] I. Affleck and A. W. W. Ludwig, Physical Review B 48, 7297 (1993).
[11] T. A. Costi, Physical Review Letters 85, 1504 (2000).
[12] T. Cichorek et al., Physical Review Letters 117, 106601 (2016).
[13] L. J. Zhu et al., Nature Communications 7, 10817 (2016).
[14] D. Gnida, Physical Review B 110, 094201 (2024).
[15] T. A. Costi et al., Journal of Physics: Condensed Matter 6, 2519 (1994).
[16] Y. Sun et al., Physical Review B 95, 235104 (2017).
[17] P. Coleman, L. B. Ioffe and A. M. Tsvelik, Physical Review B 52, 6611 (1995).
[18] R. M. Potok et al., Nature 446, 167 (2007).
[19] Z. Iftikhar et al., Nature 526, 233 (2015).
[20] J. J. Lin and N. Giordano, Physical Review B 35, 545 (1987).
[21] J. J. Lin and C. Y. Wu, Physical Review B 48, 5021 (1993). 
[22] L. Šmejkal et al., Science Advances 6, eaaz8809 (2020).
[23] J. Liu et al., Physical Review Letters 133, 176401 (2024).
[24] J. P. Ruf, Nature Communications 12, 59 (2021).

 

補記：近藤淳教授(Jun Kondo, 1930–2022)

這張照片是2017年2月6日，美國物理學會會誌Physics Today網頁版於近藤淳教授87歲生日當天，介紹他是一位固態物理學家，在1960年代中期解釋了一些金屬中的低溫電阻隨溫度下降而上升的行為時選用的照片，照片中的眼神流露著內斂沉穩與深刻的學者風采。近藤效應是我從研究生時代起不自覺地就很著迷的一個物理現象，記得我的博士論文指導教授曾說我是一個近藤效應迷。我已忘了為何喜好近藤效應，或許因為磁性雜質會破壞介觀和奈米尺度系統中的電子相位相干性(phase coherence)，致使系統失去量子干涉傳輸(quantum-interference transport)行為，所以我想瞭解。另外原因或許是因為我對近藤效應的可能維度行為感到興趣，如「近藤雲團」是一種真的物理實體嗎？又，當系統維度(如薄膜厚度，或奈米線寬度)被縮減到小於「近藤雲團」的直徑時，會出現準二維或準一維效應嗎？有趣的是，30多年來，我們實驗室從未曾發表過一篇近藤效應文章，直到2020年發表的這一篇觀測到軌道雙通道和單通道近藤效應的論文(文獻[9])。在1990年代奈米科技橫空出世，異軍突起，並帶動和開展對各種奈米材料及人工結構(如半導體量子點、原子／分子元件、碳奈米管、石磨烯等等)中的豐富多元近藤效應的研究之後(迄今仍持續不衰！) ，日本科學界和政府曾在許多年間燃起高度希望，企盼近藤淳教授能夠贏得諾貝爾物理學獎。可惜事與願違，近藤教授已在2022年以92高齡辭世。他是我非常尊敬的一位當代固態物理學家。

 

ⁱ近藤效應雖在1930年代早期就被發現，但首先確認這種電阻率通過一個極小值後，隨著溫度繼續下降而上升的行為，乃源自雜質磁矩的實驗文獻，應是M. P. Sarachik et al., Physical Review 135, A1041 (1964)，又見J. Kondo, Journal of the Physical Society of Japan 74, 1 (2005)。已故美國女性科學家Myriam Sarachik其人其事，請參考Sarachik著、陳穎叡譯〈挑戰極限：我的人生及科學之旅〉(《物理雙月刊》2020年10月30日)。所以，我們可以很簡潔地說，近藤效應問題探討的是：一個普通金屬(如銅、金)中摻雜了一顆磁性(如鐵、鉻)原子之後，會對低溫導電性質(基態)造成什麼影響？

ⁱⁱ撰寫這篇文章期間，不幸聽聞加拿大英屬哥倫比亞大學理論學家Ian Affleck教授逝世的消息，文獻[10]是他在多通道近藤效應問題的經典貢獻之一。

ⁱⁱⁱ已故Alfred Zawadowski其人其事，請參考林志忠〈學術與生活：A Matter of Tradition〉(《物理雙月刊》2019年6月26日)。

^iv朱禮軍和趙建華〈有趣的近藤效應〉(《物理》(北京)2016年7期，頁458–460)文中對軌道2CK效應的理論引述和數據解釋有待商榷，現今凝聚態物理學家的理解與共識是：在雙位能井中來回穿隧的動態結構缺陷(如原子或原子空隙)，即二能級穿隧系統(two-level tunneling systems, TLS)，不能產生軌道近藤效應，所以[6]的理論預測不成立。而且，[13]中使用的樣品為鐵磁性L10-MnAl薄膜，缺乏時間反演對稱性，破壞了自旋向上和自旋向下兩群導電電子的簡併性質，因此無從產生雙通道彼此競爭的2CK效應，詳細討論請見[8]。文獻[13]之外，請另參考L. J. Zhu and J. H. Zhao, Scientific Reports 7, 42931 (2017)。直到日前，仍有實驗文獻未密切追蹤20年來的理論進展而持續誤解引用TLS模型解釋低溫電阻上升現象，例如M. Nandi et al., Physical Review B 110, 165107 (2024)，及C. Bao et al., arXiv:2410.18689。理論方面，I. L. Aleiner和D. Controzzi (Physical Review B 66, 045107 (2002))已證明，把TLS模型中雙位能井裡的激發態都考慮進來之後，二能級系統一旦與導電電子／通道耦合，無論耦合強弱，都會因(自發性)穿隧行為而造成基態能級的明顯分裂，並使得該分裂能級之間的能距遠大於近藤特徵能量kBTK，因此TLS無法產生軌道2CK效應。（原始TLS理論認為，在適當條件下有可能找到一狹窄參數空間使得分裂能級的能距遠小於kBTK，因此存在(准)二重簡並態，發生近藤物理現象。稍後G. Zaránd (Physical Review B 72, 245103 (2005))雖試圖回應上述I. L. Aleiner和D. Controzzi的計算結果並修正原始TLS理論的缺陷，但反而導致一巨大磁阻，與實驗明顯不符，因此難以自洽。）

^v在實驗測得圖4結果之後兩三幾年，我們曾深感困惑，因數十年來的文獻一直指出二氧化釕是非磁性材料，因此理應出現軌道2CK效應。直至2019年，新研究結果發現二氧化釕具有反鐵磁性(見Z. H. Zhu et al., Physical Review Letters 122, 017202 (2019))，我們遂茅塞頓開，才瞭解時間反演對稱破缺導致了1CK效應。最近的研究則認為二氧化釕可能是(或不是)一種交變(交錯)磁性材料，請見文末結語。

^vi除二氧化銥和二氧化釕之外，在其他各種過渡金屬氧化物（例如TiO2, SnO2, VO2, SrTiO3）中，也經常出現氧空隙，這些缺陷的性質往往導致自旋、電荷和軌道自由度的相互微妙糾纏，造成各種有趣而難解的（強關聯）材料特性，是凝聚態物理學的一個長久豐富研究領域。

^vii雖低溫時電阻隨溫度下降而上升，但在較高溫時，電子—聲子散射才是造成金屬電阻的主要原因。因此從低溫逐漸提升溫度時，電阻會通過一個極小值，因為電子—聲子散射率隨溫度上升(晶格原子振動越趨激烈)而增強，見圖一和二。在提出理論解釋近藤效應的首篇文章裡，標題即是“Resistance minimum in dilute magnetic alloys”，見J. Kondo, Progress of Theoretical Physics 32, 37 (1964)。

^viii請參考Editorial, Nature Physics 10, 329 (2014).