
來自巴塞爾的數學天才
這個系列到目前為止,已經介紹了三位在形塑解析力學過程中有重大貢獻的科學家。這一集要介紹的這位,其實已經在前三集中已經不斷露臉,但是這一次我們要從他的視角,來看解析力學成型的過程,因為他可以算是塑造解析力學的過程中,最重要的推手,說他是塑造解析力學的mastermind 也不為過,他就是被譽為十八世紀最偉大的數學家,萊昂哈德·尤拉(Leonhard Euler, 1707年4月15日—1783年9月18日)。他是有史以來最為多產的數學家,但是他在物理學的功績,絕對不亞於他在數學的建樹。但是他在物理學的貢獻,相對來講,並不廣為人知。所以這一次就讓阿文好好地為你說清楚,講明白吧!
要介紹尤拉之前,必須先介紹一下科學史上赫赫有名的白努利家族。白努利(Bernoulli)是一個在瑞士巴塞爾的經商學者家族。家族的開基祖,萊昂·白努利於16世紀從當時歐洲最富有的商業城市,安特衛普,移民到巴塞爾。很多藝術家和科學家都出自白努利家族,其中最有名的是雅各·白努利(Jakob I. Bernoulli,1654—1705)和他的弟弟約翰·白努利(Johann Bernoulli,1667—1748)還有約翰的兒子丹尼爾·白努利(Daniel Bernoulli,1700—1782),這三人都跟尤拉結下不解之緣。
萊昂哈德·尤拉的父親,保羅·尤拉,曾在巴塞爾大學學習神學,並在那裡上過雅各‧白努利的課。 事實上,保羅·尤拉和約翰·白努利在巴塞爾讀大學時,都曾住在雅各·白努利的房子裡。保羅·尤拉後來成為新教牧師,並與另一位新教牧師的女兒,瑪格麗特·布魯克結婚。他們的兒子萊昂哈德·尤拉在巴塞爾出生,萊昂哈德是家中4個孩子中的長子,他有兩個妹妹安娜瑪麗亞(Anna Maria)和瑪麗亞·馬格達萊娜(Maria Magdalena),還有一個弟弟約翰·海因里希(Johann Heinrich)。在萊昂哈德一歲時,尤拉全家搬到了里恩,萊昂納德就是在離巴塞爾不遠的里恩長大的。正如我們所提到的,保羅·尤拉接受過一些數學訓練,所以他能夠教小尤拉一些初等數學。萊昂哈德八歲時被送往巴塞爾上學,在此期間他與外祖母一起生活。從各方面來看,小尤拉上的那所學校都不怎麼出色,尤拉根本沒有從課堂上學到任何數學。萊昂哈德對數學的興趣無疑是被父親的教學所激發的。他自己閱讀了數學書籍,並且參加了一些私人課程。保羅·尤拉原本打算叫兒子跟隨他進入教會工作,把他送到巴塞爾大學,就是為了他未來在教會的服侍做準備。 1720 年,14 歲的尤拉進入巴塞爾大學就讀。但是小尤拉根本是個數學天才,約翰·白努利很快就發現尤拉在數學方面的巨大潛力。 尤拉在其未出版的自傳中是這麼回憶的:
……我很快就找到了一個機會,被介紹給著名的約翰·白努利教授。 ……確實,他很忙,所以斷然拒絕替我上私人課的請求; 但他給了我更有價值的建議,他建議我開始自己閱讀更困難的數學書籍,我盡己所能勤奮地學習,後來當我遇到障礙或困難的話,他會在每週日下午接待我,很友善地向我解釋我無法理解的一切...
1723 年,尤拉寫了一篇比較笛卡兒和牛頓哲學思想的論文,以此拿到哲學碩士學位。 1723年秋天,他按照父親的意願開始學習神學,但是,儘管他一生都是虔誠的基督徒,但他在希臘文和希伯來文中找不到他對數學的那種熱情。在約翰·白努利的勸說下,尤拉的父親勉強地同意,讓尤拉轉去學習數學。如果約翰·白努利不是老尤拉在大學期間的朋友,老尤拉應該不是那麼容易說服的吧。尤拉很快地在 1726 年完成了一篇題為《De Sono》的論文,內容是研究聲音的傳播,以此拿到了博士學位。他在巴塞爾期間遵循約翰·白努利的建議,鑽研了許多數學著作。 其中包括瓦里尼翁、笛卡兒、牛頓、伽利略、范斯庫頓、雅各·白努利、赫爾曼、泰勒和沃利斯的作品。 1726 年,尤拉還發表了另一篇論文,那是一篇關於有黏滯力的介質中的等時曲線的短文。 1727 年,他發表了另一篇關於互易軌跡(reciprocal trajectories)的數學論文,並且提交了一份關於船上桅杆最佳佈置的文章,這篇論文還參加了1727年巴黎學院大獎競賽。1727 年的獎項頒給了擅長船舶設計的數學家皮耶·布格(Pierre Bouguer,1698—1758),尤拉得到了第二名,這對年輕的畢業生尤拉而言,是一項相當了不起的成就。獲得首獎的皮耶·布格後來成為法國科學院幾何學副教授,1735年布格跟隨夏爾·瑪麗·德·拉孔達明(Charles Marie de La Condamine)前往秘魯進行大地測量,確認了赤道附近子午弧的角度。這個任務耗時十年,所有的研究成果都由布格在1749年以書籍《La figure de la terre》發表。在該書中,布格提到在秘魯高海拔地區測得的重力值小於理論計算值,首次發現了重力異常。1746年布格發表了第一本造船工程專書《Traité du navire》 ,在該書中布格首次以重心高度來解釋船舶的穩定性。他之後的著作幾乎都是關於航海和造船工程的理論。尤拉敗在這樣老練的競爭者手上似乎也是意料中事。
不過尤拉真正的挑戰是必須為自己找到一個學術職位,1725年,約翰·白努利的長子,尼古拉·白努利和次子,丹尼爾·白努利都進入位於聖彼得堡的俄國皇家科學院工作,同時他們向尤拉保證,稱如果職位有空缺,他們馬上會推薦尤拉。1726年7月31日,來到俄國不到一年的尼古拉就不幸因闌尾炎去世,於是丹尼爾便接替了他哥哥在數學和物理學部門的職位,同時依照約定,推薦尤拉來接替他自己原先在生理學的職位。尤拉於 1726 年 11 月接受了這一職位,但表示他不想在第二年春天之前就前往俄羅斯。 他有兩個拖延的理由。第一,他想要爭取時間研究與他的新職位相關的主題,但是第二的原因更重要,他對巴塞爾大學找到位置一事,仍然不死心,因為前陣子那裡的物理學教授去世了。尤拉在爭取這一職位時寫了一篇關於聲學的文章,後來成為經典之作,但是他還是沒有被選中。幾乎可以肯定的是,他的年齡(當時他19歲)是致命傷。
當尤拉知道自己確定沒有機會在巴塞爾大學找到教職後,才於1727 年4 月5 日離開巴塞爾。不過事後看來,塞翁失馬,焉知非福,因為這項決定迫使他從一個小小的共和國搬到一個更適合他的研究環境。尤拉乘船沿著萊茵河而下,乘坐郵政馬車穿越德國各州,然後從呂貝克乘船抵達聖彼得堡。1727 年 5 月 17 日。在彼得大帝的妻子葉卡捷琳娜一世創建聖彼得堡科學院兩年後,他加入了該院。 在丹尼爾·白努利和雅各布·赫爾曼的要求下,尤拉被任命到科學院的數學物理部門,而不是最初提供給他的生理學職位。當時的聖彼得堡可謂群英薈萃,除了與尤拉有個人情誼的幾何學家雅各布·赫爾曼(Jakob Hermann),丹尼爾·白努利(Daniel Bernoulli)以外,多才多藝的學者,克里斯蒂安·哥德巴赫也在那裡,他在應用數學領域與尤拉有共同的興趣,尤拉常與他討論了許多分析和數論問題。法國的天文學家和地理學家約瑟夫-尼古拉·德利爾(Joseph-Nicolas Delisle,1688—1768)當時也在聖彼得堡創建並管理天文學學校,在這樣優越的環境下,尤拉可以說是得其所哉了。
1727 年至1730 年間,尤拉名義上在俄羅斯海軍擔任醫官,官拜中尉。在聖彼得堡,他與丹尼爾·白努利住在一起。其實當時丹尼爾·白努利在俄羅斯已經住到快抓狂了,他要求尤拉從瑞士给他帶茶、咖啡、白蘭地和其他美味佳肴給他。當時丹尼爾是俄國皇家科學院數學高級主任,他最終還是受不了俄羅斯無聊的生活而在1733 年離開聖彼得堡返回巴塞爾,於是尤拉被任命為數學高級主任。 這次任命帶來的調薪使尤拉得以結婚,他於 1734 年 1 月 7 日與聖彼得堡一位畫家的女兒卡塔琳娜·格塞爾結婚。卡塔琳娜和尤拉一樣,都是來自瑞士。 他們共有 13 個孩子,但只有 5 個撐過嬰兒期。 尤拉後來聲稱,當年他懷裡抱著一個嬰兒,其他孩子在他腳邊玩耍,正是他做出了一些最偉大的數學發現的時候。
尤拉在1730 年之後的研究計劃包羅萬象,數論、分析學、微分方程式和變分法都包含在內。但是對後代物理學家影響最大的當然還是我們的主題:解析力學。尤拉在1736 年出版的《力學,運動的科學的解析闡釋Mechanica sive motus scientia analytice exposita》,為力學帶來了重大進步,在力學的歷史中是足以媲美牛頓的《自然哲學的數學原理》的重要著作!尤拉的《力學》首次以數學分析的形式來闡述牛頓力學,開啟了尤拉的主要數學工作之路。
正如蘇聯科學史家,尤什克維奇(Adolph-Andrei Pavlovich Yushkevich, 1906-1993)寫的:-
與他的前輩相比,尤拉在力學方面的研究的顯著特徵是分析的系統和成功的應用。 以前的力學方法大多是採用綜合和幾何的方法; 他們要求採取過於個人化的方法來解決不同的問題。 尤拉是第一個認識到把統一的分析方法引入力學的重要性的科學家,從而使其問題能夠以清晰和直接的方式來解決。
沒錯! 我們熟悉的牛頓力學的形式正是尤拉所賦予的。尤拉正是第一個將力寫成動量對時間微分的形式。所以牛頓力學的任務變成了求出微分方程的解。特殊函數和微分方程式對於解析力學特別重要,因為它們提供了解決具體問題的工具。舉例而言,尤拉考慮了真空中和阻力介質中的質點的運動。他也分析了中心力作用下的質點的運動。為了處理任意形狀表面上質點的運動他還必須解決微分幾何和測地線相關的各種問題。所以尤拉研究了曲面理論和曲面曲率。尤拉在這一領域未發表的許多成果後來都被高斯重新發現。
說到幾何,尤拉有一項開創性的發現不能不提:U.那就是他在1736年解決的柯尼斯堡七橋問題,尤拉還發表了論文《關於位置幾何問題的解法》(Solutio problematis ad geometriam situs pertinentis),闡述如何解決一筆畫問題,這篇論文是最早運用圖論和拓撲學的典範。尤拉還發現了有關凸多面體的尤拉公式: V - E + F = 2。這個公式給出凸多面體的頂點(Vertex, V),邊(Edge, E)和面(Face, F)必須滿足的關係,因此,對一個平面圖形。此公式中的常數χ被稱為是尤拉示性數,單連通流形(例如球面或平面)的尤拉示性數是2。即使將圖形或凸多面體加以壓縮,拉長,或是其他的形變,只要不打洞,掐斷,那麼這個數值都不會改變。這種在連續映射下不會改變的幾何性質,後來被稱為拓樸性質,而尤拉正是拓樸學的先驅呢。
另一項尤拉開創的新領域則是變分法。他於 1740 年出版的著作 《Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, sive solutio problematis isoperimetrici lattissimo sensu accepti一種尋找具有最大或最小屬性的曲線的方法,或在最廣泛接受的意義上解決等周問題的方法》開始了對變分法的研究。尤拉對這個主題的主要貢獻是將其從對本質上特殊情況的討論轉變為對非常普遍的問題類別的一般性討論。本書列出了 100 個特殊問題來說明他的方法。尤拉也示範了如何寫出所謂的「尤拉微分方程式」的一般過程。尤拉用來展現他方法威力的問題為:(1)在所有平面曲線y = y(x)、0 ≤ x ≤ a 中找到最大化或最小化∫Z dx 的曲線,其中Z 是「確定的” x、y 和 y 導數的函數; (2)求阻力介質中最短時線和等時線的形狀; (3) 求給定凹面或凸面上連接兩個固定點的測地線。在解決測地線問題時,尤拉發現了拉格朗日乘子法的一個簡單實例。這本書也是首次提出最小作用量原理的著作,尤拉將其表達如下:對於給定的投影體,以 M 表示其質量,以 v 表示其速度的平方的一半,以 ds 表示弧長元素。然後,在通過同一對端點的所有曲線中,所需曲線是使積分 ∫Mvds 最小的曲線。一百多年後,數學家卡拉西奧多里 (Constantin Carathéodory,1873-1950) 認為這篇論文是:
……有史以來最美麗的數學著作之一。
尤拉認為微分方程式,變分法與解析力學三個領域密切相關,因為解析力學就是利用變分法將最小作用量原則轉化成為微分方程式,這導致尤拉對微分方程式進行了廣泛的研究。他開發微分方程式的冪級數解、常數變分法、積分因子、逼近解法等等,這些都是他從解決具體物理問題時得到靈感的,像是他在考慮振動膜的問題時,尤拉得出了貝塞爾方程式,他透過引入貝塞爾函數來求解。那麼為何貝塞爾函數不叫尤拉函數呢? 一來尤拉發明太多函數了,再者他也沒有全面研究這種函數的性質,直到1816 年,弗里德里希·威廉·貝塞爾 (Friedrich Wilhelm Bessel,1784−1846) 證明,貝塞爾函數展開式中的係數可以給出積分表示。 到了1824 年,貝塞爾進一步對這些函數進行了全面研究,所以這些函數現在被稱為貝塞爾函數。
由於開發微分方程式的冪級數解,無疑地讓尤拉成了級數求和的高手。尤拉年輕時最出名的結果是他解決了後來被稱為巴塞爾問題的問題。 這是為了找出無限級數總和的封閉形式 :
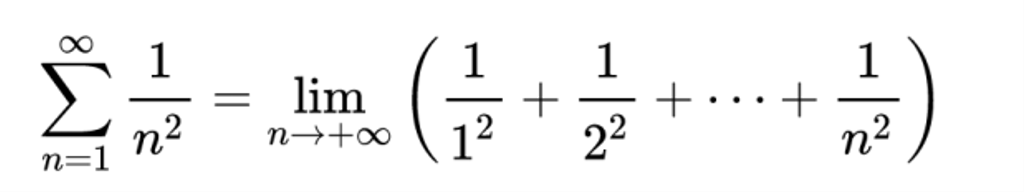
尤拉在 1735 年證明了這個級數的極限是 π2/6,這個問題曾經難倒了許多頂尖數學家,包括雅各·白努利、約翰·白努利和丹尼爾·白努利。 萊布尼茲、史特林、德莫弗爾等人也曾研究過這個問題,但沒有成功。但他繼續證明了很多類似的級數,他進一步在1737 年證明了 zeta 函數與質數序列的聯繫,給出了著名的關係式,這讓尤拉聲名大噪。尤拉在無限級數方面所做的其他工作還包括在 1735 年引入他著名的尤拉常數 γ,他證明該常數是他將常數γ計算到小數點後16位。 尤拉也研究了傅立葉級數,並在 1744 年第一個用這樣的級數表達了代數函數,並給出了結果。在寫給哥德巴赫的信中,與尤拉的大多數工作一樣,結果發布之前有相當長的一段時間的延遲。 這項結果直到 1755 年才發表。1736 年 6 月 8 日,尤拉寫信給詹姆斯·斯特林,告訴他有關冪倒數求和、調和級數和尤拉常數以及其他級數結果的結果。 他特別寫道:-
關於非常緩慢收斂的級數的求和,在過去的一年裡,我向我們的學院講授了一種特殊的方法,透過這種方法,我毫不費力地足夠準確地給出了許多級數的求和。
然後,他繼續描述了現在所謂的尤拉-麥克勞林求和公式。 兩年後,史特林回覆告訴尤拉,麥克勞林:
……將出版一本關於流數的書。 ……他有兩個通過項的導數求和級數的定理,其中一個與你發給我的結果相同。
尤拉回答:
……我不希望任何事物有損著名的麥克勞林先生的名聲,因為他可能在我之前發現了相同的求級數定理,因此值得被稱為它的第一個發現者。 因為我大約四年前發現了這個定理,當時我也向我們學院更詳細地描述了它的證明和應用。
由此可見尤拉敦厚的人品。這樣的老實人應該不會料到他的下半生會不斷地跟人吵架吧!
這個時期的尤拉除了在純數學有眾多成就以外,他也同時涉及眾多的實用計畫,包括製圖、科學教育、磁學、消防車、機器,甚至造船!製圖學是尤拉在1735 年被任命為聖彼得堡學院地理部主任後涉足的另一個領域。他的具體任務是幫助德萊爾繪製整個俄羅斯帝國的地圖。 《俄羅斯地圖集》是這次合作的成果,於 1745 年問世,由 20 張地圖組成。 該書出版時,尤拉在柏林自豪地指出,這部著作使俄羅斯人在製圖藝術方面遠遠領先德國人。
至於造船則是來自尤拉對力學的研究,他在《力學》之後出版了兩卷關於海軍科學的著作,這兩卷書在理論和應用力學方面都極其出色,尤拉展現了他對船舶推進問題的大量研究。他甚至應用變分原理來確定最佳船舶設計,並首先建立了流體靜力學原理。自阿基米德以來就有人研究流體靜力學,但尤拉給了一個明確的版本。尤拉在這裡也開始開發剛體的運動學和動力學,雖然完整的理論要等到未來才發表。除此之外,尤拉也發表了關於音樂理論的文章,特別是他於 1739 年出版了《 新音樂理論的嘗試Tentamen novae theoriae musicae 》,其中他嘗試創作音樂:-
……數學的一部分,並從正確的原理中有序地推導出一切可以使音調組合在一起和混合令人愉悅的東西。
然而,根據,這項工作是:
……對音樂家來說數學太先進,對數學家來說音樂性太強。
顯然尤拉的感性還不足以成為音樂家吧。
也許就是尤拉工作過度,他的健康也開始出了問題。尤拉的健康問題始於1735年,當時他發高燒,差點喪命。 然而,他並沒有向他的父母和巴塞爾的白努利家族成員透露這個消息,直到他康復為止。 尤拉在他的自傳體著作中說,他的視力問題始於 1738 年,由於他的製圖工作導致過度疲勞,到 1740 年他出現了 :
……失去了一隻眼睛,[另一個]目前可能處於同樣的危險中。這讓他的晚年陷入一片黑暗。
在聖彼得堡的這段時間,尤拉於1738年和1740年連續兩次獲得巴黎學院大獎,雖然兩次他都與其他人分享了第一名,但是他已經名滿全歐了。他的聲名遠播,所以普魯士剛登基的腓特烈二世向他發出邀請。起初尤拉並沒打算離開聖彼得堡。 然而,當時俄羅斯政局動盪,使得外國人的處境變得日益困難,這促使尤拉改變了主意。所以他最後回應了腓特烈二世的邀請,前往柏林。尤拉於 1741 年 6 月 19 日離開聖彼得堡,於 7 月 25 日抵達柏林。尤拉在柏林迎來了他人生真正的高峰,卻也招來了許多麻煩,欲知詳情的看官們,還請稍待下回分解!
參考資料
(一)中文,德文,英文維基相關條目
封面照片取自 維基百科 由雅各布·伊曼紐爾·漢德曼 - 2011-12-22 (upload, according to EXIF data), 公有領域,https://commons.wikimedia.org/w/index.php?curid=1001511

