黑洞，一直是科幻作品與物理學界熱議的話題。它的提出可以追溯到數世紀之前，並在上個世紀初次得到理論上的支持。隨著天文觀測技術的飛躍，直至2019年，科學家們首次透過「事件視界望遠鏡」(Event Horizon Telescope, EHT)捕捉到了人類歷史上首張黑洞影像——來自位於M87星系中心的超大質量黑洞。隨後，在2022年，我們所居住的銀河系中央的黑洞——人馬座A*的影像也正式公開。從黑洞理論的奠基到首度被拍攝到，間隔了約一個世紀，但這也說明了人類對於黑洞的理解又更近了一步。本文將從廣義相對論的觀點探討奇異點的概念、以及從黑洞的內部結構衍生出的各種可能性。
製造黑洞的上限
如果要認識黑洞，那麼我們必須先知道一個關鍵概念——「史瓦西半徑」(Schwarzschild radius)。任何具有質量的物體，只要被壓縮到某個特定的極限值就會坍縮成黑洞，而這個臨界值就是史瓦西半徑。例如，一個太陽質量的天體史瓦西半徑約為三公里；類似地，地球若被壓縮至一枚銅板大小，也將成為黑洞。此半徑有不少推導方式，其中最簡單的可以透過基本的動能與重力位能方程推導而來：
$$\frac{1}{2}mv^2 \geq \frac{GMm}{r}$$
不等式的左半邊是動能、右半邊則是重力位能。假設你（或者任何考慮落入黑洞的物體）的質量是m、星體的質量則是M，這個式子描述了一個質量m的物體需要多大動能才能從M自身的重力場逃脫。現在，我們只需要把速度v代換成宇宙最快的速限——光速c，不等式就會變成：
$$\frac{1}{2}mc^2 \geq \frac{GMm}{r_s}$$
我們便能直接解出臨界半徑
$$r_s = \frac{2GM}{c^2}$$ (1)
這就是「史瓦西半徑」：一旦質量M被壓縮到小於這個半徑值，那麼其所產生的重力場將連光線也無法逃逸，形成所謂的黑洞。在天體物理學中，恆星演化末期往往會邁向戲劇性的結局，對於大質量恆星而言，一旦核心超過了約3倍太陽質量、突破所謂的「奧本海默極限」(Tolman-Oppenheimer-Volkoff limit)，電子與中子簡併壓力將無法支撐，從而將坍縮成黑洞。
後來，人們逐漸習慣把史瓦西半徑聯想成黑洞的半徑、定義了黑洞的大小。所有黑洞都擁有對應的史瓦西半徑，而當你跨越這個界線時，即使以光速運行，也將無法返回——這條邊界就是「事件視界」(event horizon)。你可以將其想像為一艘漂向瀑布邊緣的小船，一旦越界，便無法逆流而上，只能直墜深淵。
那麼，掉入黑洞後，會發生什麼事？由於強大的重力場會讓時空劇烈彎曲，時間和空間的概念將會超乎尋常，但撇除你的體驗有多刺激，最終的結果通常會是一樣的——你將落入「奇異點」(singularity)被絞碎。
奇異點：物理學的死穴？
1915年，愛因斯坦提出廣義相對論，其中最核心的數學描述便是「愛因斯坦場方程式」(Einstein field equations)：
$$R_{\mu\nu} - \frac{1}{2}g_{\mu\nu}R = \frac{8\pi G}{c^4} \, T_{\mu\nu}$$ (2)
看起來確實有點複雜，在這裏我們先不探討它的數學意義，只需知道：這條方程式的等號左邊描述了時空的彎曲，而右邊則代表物質的運動。簡單來說它揭示了：物質決定了時空如何彎曲，而時空的彎曲則決定了物質如何運動。在廣義相對論的視角下，重力並非一種傳統意義上的力，而是一種時空的幾何效應。
誠如看上去那樣，這條方程式極為複雜，但在特定情境下還是可以得到精確解。例如，假設重力場是球對稱、無旋轉且不帶電，對應的解便是「史瓦西度規」(Schwarzschild metric)：
$$ds^2 = -\left(1 - \frac{2GM}{c^2 r} \right) c^2 dt^2 + \left(1 - \frac{2GM}{c^2 r} \right)^{-1} dr^2 + r^2 d\Omega^2$$ (3)
我們可以簡單拆分來看：$dt^2$ 項描述了重力場中時間如何被影響，$dr^2$ 項描述了空間如何被扭曲，最後 $d\Omega^2 = d\theta^2 + \sin^2\theta\, d\phi^2$ 項說明了球對稱性——諸如恆星或黑洞周圍的時空結構，都可以用史瓦西度規來描述。
但在某些情況下，這個解是會發散的、也就是會出現「無窮大」這種物理與數學家並不樂見的結果。直觀來看，半徑 $r$ 有兩種可能性會導致發散——第一種是：
$$r = \frac{2GM}{c^2} = r_s$$ (4)
是的，其實就是前面提過的「史瓦西半徑」。把它帶進去就會得到發散的 $ds^2$，但物理學家很快就發現，其實這只是座標系的問題（下文會說明），也就是換一套座標系統後、就沒事了，因此 $r = r_s$ 並不是嚴格意義上的「奇異點」。我們也已經知道了，$r = r_s$ 就是事件視界，我們永遠無法得知視界內部的情況，因此它比較像是一種時空的分隔線、而不是曲率無窮大的位置。順帶一提，在廣義相對論中，其實還有一套可以用來檢查時空曲率是否「真正」發散的工具——「克雷希曼純量」（Kretschmann scalar）：
$$R_{\mu\nu\rho\sigma} R^{\mu\nu\rho\sigma} = \frac{48 G^2 M^2}{r^6}$$ (5)
讀者不必煩惱左半部的物理意義，只需把式(4)代入，便會發現最後給出的仍然是有限的解。
然而，另一個情況下，似乎就不是那麼樂觀了，那就是：
$$r = 0$$ (6)
把它代入史瓦西度規 (3) 會得到發散的結果，即使代入克雷希曼純量 (5)，也依然是發散的——這就意味著：時空在 $r = 0$ 處確實是發散的，也就是真正的「奇異點」！用白話一點的說法，$r = 0$ 就是一個重力場、密度、時空的曲率「無窮大」的「點」。對數學家來說，「無窮大」和「點」本身就不是一個靠譜的概念，畢竟再大都得有個上限、再小也都該有個體積，然而 $r = 0$ 的確是無法透過任何座標變換來消除的。這也就是為什麼科普文章中，所有物質落入黑洞後都會被奇異點絞碎，因為說到底我們根本無法得知 $r < r_s$、也就是越過事件視界後的情況；我們只知道該處時空彎曲的程度足以導致時間與空間的角色互換，此時你的未來將不可避免地趨向黑洞最深處的 $r = 0$——一個現有物理定律無法描述的所在。
是的，從現有的廣義相對論觀點來看，$r = 0$ 不僅僅是黑洞的盡頭，也是物理法則的終點。
此路不通？換個座標系來試試
還記得嗎？上一段我們提到史瓦西解存在兩種可能性，其中第一種可能性（$r = r_s$）雖然會讓度規發散，但透過適當選擇座標系後就可以有效消除。我習慣這樣比喻：人類使用了經度來劃分地球上不同位置的時區，但「經度」的概念在南、北極點將變得無法適用；雖然從地球儀上看來，所有經線都會匯聚在北極點，但這並不表示你走上北極點的時候你的手錶時針會跳轉失靈。
在黑洞的情境中，$r = r_s$ 其實也是座標系的選擇問題，我們可以透過變換座標系來阻止發散。其中一種方法是使用「克魯斯卡爾座標系」（Kruskal–Szekeres coordinates），展現了史瓦西解的「最大解析延拓」，簡單來說，你可以把它想像成將黑洞的時空結構圖完整展開，此時事件視界不再顯示出發散性，而是變成時空中的一條分隔線，而奇異點則對應於一對雙曲線。
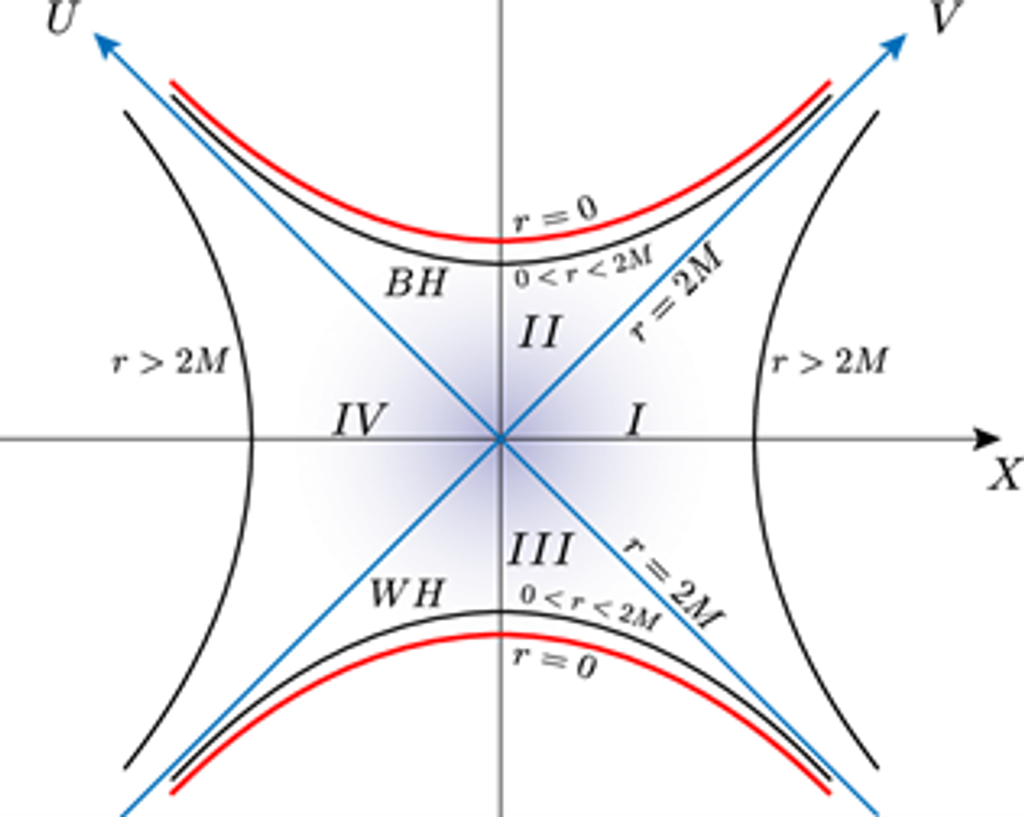
圖1：克魯斯卡爾座標系中，黑洞的時空結構可以被劃分成四個區域。（Source: ResearchGate, https://www.researchgate.net/figure/Kruskal-Szekeres-diagram-of-S-4_fig2_337531856）
數學細節暫且不論，我們可以從克魯斯卡爾圖中看到時空被劃分為四個區域（如圖1所示）：
- 區域 I ：我們熟悉的宇宙（本宇宙）。
- 區域II：是黑洞內部，由於縱軸代表時間流向，因此一旦進入黑洞（區域 II）的事件視界，就無可避免地會撞上奇異點（上方的雙曲線）。
- 區域III：與黑洞對稱的區域，其內部的物質無法回到黑洞，而是注定遠離奇異點（下方的雙曲線），最終進入我們的宇宙（區域I）或另一個時空（區域 III）。這個假想上與黑洞性質完全相反的區域又被稱為「白洞」(white hole)。與黑洞不斷吸收物質不同，白洞則是持續噴湧物質，某些理論甚至認為宇宙誕生的大霹靂(Big Bang)可能就是一個白洞。然而，白洞目前仍然只是一種數學上的推論，它本質上是黑洞的「時間反演」，但這也可能導致與熱力學第二定律相悖。
- 區域IV：與本宇宙（區域I）對稱、對應於另一個獨立的「鏡像宇宙」。在理論上，物質可以從白洞（區域 III）流入我們的宇宙（區域 I）或鏡像宇宙（區域IV），但無法逆行穿過白洞的事件視界，因為時間流向不允許這種過程發生。
正所謂「山重水復疑無路，柳暗花明又一村」，克魯斯卡爾座標系在數學上揭示了奇異點也許並非黑洞盡頭的可能性。
黑洞的時空結構，可能遠比想像中來得複雜？
克魯斯卡爾圖的可視化方式進一步催生出了「潘洛斯圖」（Penrose diagram），它能夠更直觀地展現時空區域之間的因果關係：
- 在圖中，光速對應於 45 度的對角線，這也是事件視界所在的位置。
- 奇異點則被描繪為位於未來（上）與過去（下）的波浪線。
與克魯斯卡爾圖相同，潘洛斯圖表明，任何落入事件視界的物體最終都無法避免撞上奇異點（謹記時間軸是向上的縱軸），從而使黑洞的因果結構一目了然。
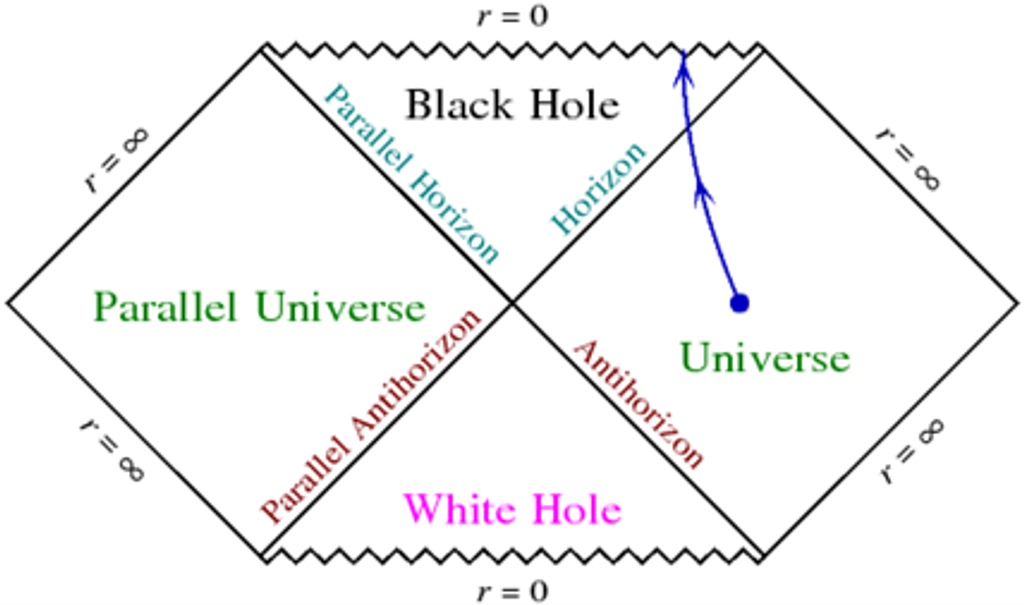圖2：黑洞的潘洛斯圖。（Source: https://jila.colorado.edu/~ajsh/insidebh/penrose.html）
在克魯斯卡爾座標系的潘洛斯圖中，你或許會產生一個疑問：我們是否能從自身所處的宇宙（圖1的區域I）直接穿越到對應的平行宇宙（區域IV）？事實上，這兩個區域之間的假想通道在歷史上被稱為「愛因斯坦-羅森橋」(Einstein-Rosen bridge)，後來物理學家約翰·惠勒(John Wheeler)為其取了一個更通俗的名稱——「蟲洞」(wormhole)。順帶一提，「黑洞」這個名詞最早也是在惠勒的一次會議上提出的。
從潘洛斯圖（圖2）可以看出，這種愛因斯坦-羅森橋的開口只允許在空間中的水平穿越（因為縱軸是時間），也就是說，它屬於「類空」(space-like)蟲洞。這意味著，想要通過它，你必須在「瞬間」完成穿越、甚至可能需要超光速運動——而這將違反因果律，因此在物理學上是不可能實現的。
但因為我們目前討論的是靜態黑洞的解，即史瓦西黑洞的情況。如果我們考慮旋轉的「克爾黑洞」(Kerr black hole)、帶電的「萊斯納-諾德斯特姆黑洞」(Reissner-Nordström black hole)，或者同時具有旋轉與電荷的「克爾-紐曼黑洞」(Kerr-Newman black hole)，那麼情況就可能變得不同！
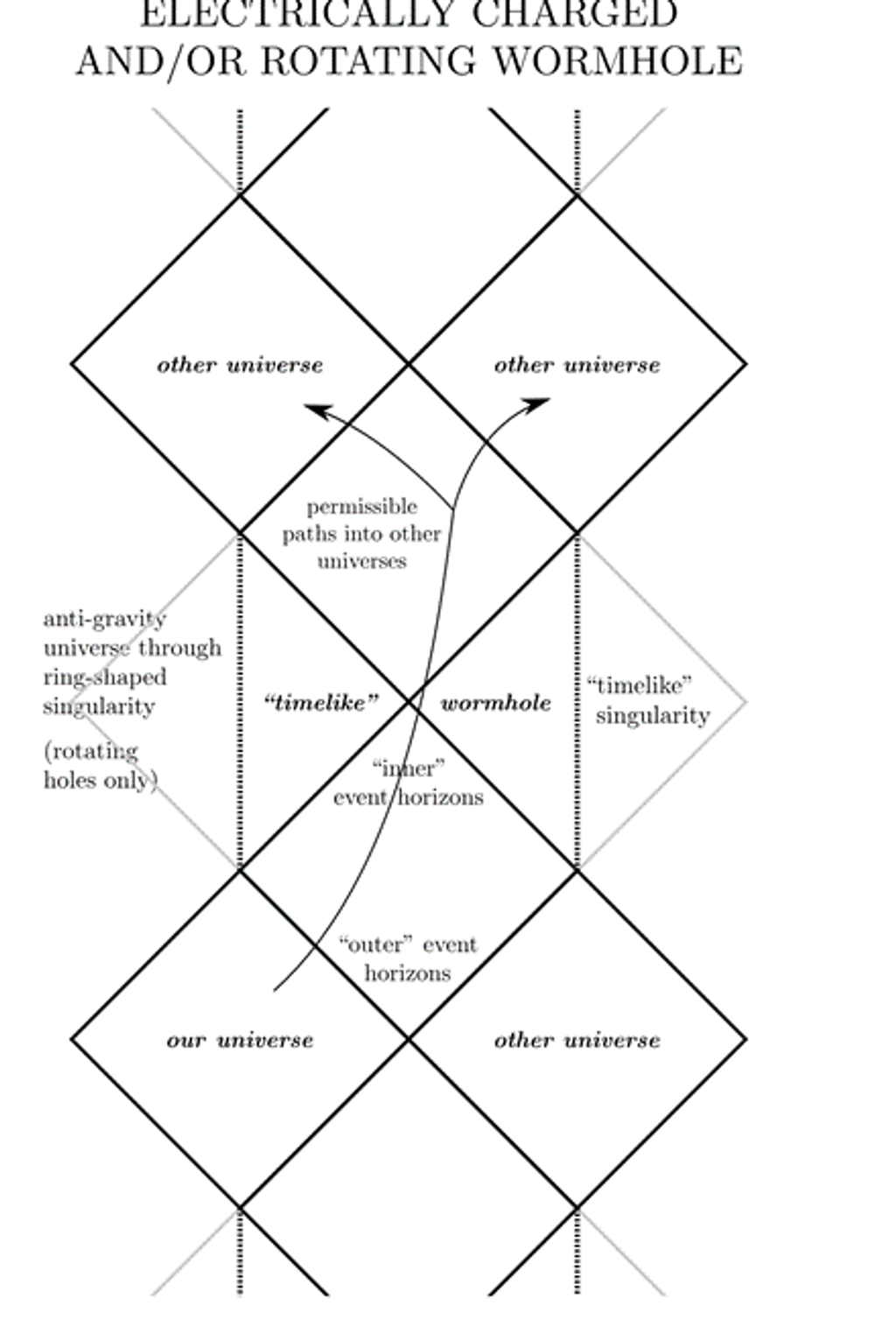
圖3：帶電黑洞的潘洛斯圖。若是旋轉帶電黑洞，則會多出奇異環的結構（Source: Wikipedia）
這些黑洞的時空結構更加複雜（圖3），可能會出現內、外層事件視界，甚至還有奇異環(ring singularity)這樣的結構。從潘洛斯圖來看，這類黑洞的時空可能允許「類時」(time-like)蟲洞的存在，即通道沿著時間軸（縱軸）方向開放、允許物體在有限的時間內穿越並抵達未來。
此外，帶電黑洞的潘洛斯圖詮釋了「鏡像宇宙」在數學上存在的合理性。而在某些旋轉黑洞的解中，穿越奇異環甚至可能通向一個遵循不同物理法則的「反宇宙」(negative universe)。
這些看似科學又更像科幻題材的概念往往引人入勝，然而它們都是「理論中的理論」，蟲洞、白洞、平行宇宙的存在仍未被證實。即便蟲洞確實存在，也極可能非常不穩定，甚至微小的擾動——例如你身上的一顆電子——都可能導致其崩塌。因此，與其將潘洛斯圖視為多重宇宙之間的地圖，不如將其當作一種工具、幫助我們更直觀地理解時空結構，這樣的視角或許更具實際意義。
但無論如何，從愛因斯坦場方程式的提出、史瓦西度規的解、一直到克魯斯卡爾座標系以及潘洛斯圖的發明，人們也逐漸意識到：黑洞內部的時空結構，其實可能遠比想像中來得更錯綜複雜。
而在20世紀廣義相對論奠基後，短短數十年間，黑洞也從以前被視為最令人頭疼的知識領域、到後來掀起了一陣陣研究熱潮；甚至在量子場論逐漸鞏固後，物理學家發現黑洞具有一些耐人尋味的量子性質，這也讓黑洞成為了研究廣義相對論與量子力學的重要窗口。
參考文獻
● S. M. Carroll (2019). Spacetime and geometry: An introduction to general relativity. Cambridge University Press.
