首先讓我們複習一下質量與電子伏特（electron volt, eV）的概念。粒子物理學中，電子伏特相當於一顆電子在一伏特電壓下所帶的能量，約為 $1.602 \times 10^{-19}$ 焦耳。質能等價公式（$E = mc^2$）意味著質量與能量是一體兩面的，因此粒子物理學通常會省略常數 $c$，直接將質量用 eV 等單位來表示。電子與原子核之間的能級差約在 eV 尺度，這個能量大約就是將電子彈出原子的大小；假設原子核的束縛能落在 MeV，那麼一旦擁有 MeV 級的能量，就可以拆散原子核。對於日常生活而言，我們可能很難感知這個能量有多強大，畢竟：即使能量高達 $1\ \mathrm{GeV} \simeq 1.602 \times 10^{-10}$ 焦耳，但現實中一顆果子從樹上掉下來的能量大約就是 $1$ 焦耳、將近 $10^{10}\ \mathrm{eV}$（$10\ \mathrm{GeV}$）了——所以我們應該用微觀的角度想：假設一顆蘋果由 $10^{25}$ 個基本粒子所組成，如果每個粒子都擁有 $10\ \mathrm{GeV}$ 的能量，蘋果所攜帶的總能量將高達 $10^{35}\ \mathrm{eV}$，相當於 $10^{16}$ 焦耳——這個能量大概可以撞出直徑一公里的隕石坑了！
      在上一篇文章中，我們提及了微中子探測的歷史沿革、以及微中子一些耐人尋味的神奇性質。本篇文章將帶領大家探索微中子最核心的議題——微中子振盪、以及微中子如何挑戰現有的物理學模型。

一、謎之質量？——微中子振盪

       從1960年代的實驗探測、一直到2015年的諾貝爾物理學獎，「微中子振盪」(neutrino oscillation)這個議題逐漸浮上檯面，同時也指出了一項事實：微中子的質量並不為零。這也意味著——定義出微中子與身俱來「質量為零」的粒子物理標準模型恐怕將需要改寫。

      不過，想必不少讀者會好奇：「微中子振盪」為什麼意味著微中子具有「質量」？雖然對於微中子質量的生成機制我們尚未有個明確的論述，但微中子振盪倒是容易解釋得多，甚至用基礎的量子力學就足以說明。一言以蔽之就是：微中子振盪源於「微中子的質量與味特徵態(eigenstate)得以被區辨」這個假設。粒子物理學背後是場論的框架，場論的基礎是量子力學，而量子力學則是建構在向量空間之上。量子力學告訴我們粒子有各種不同的狀態（特徵態），其行為透過觀測所決定，不同的物理行為也會呈示出不同的表徵；就像是你在家說中文、在國際會議時就得說英文一樣，對於微中子而言，在自由空間傳播時會以「質量特徵態」描述、參與弱交互作用時則用以「味特徵態」描述。而我們所觀測到的微中子，其實也是不同特徵態的混合：如果用紅、綠、藍三原色來描述微中子的質量或味特徵態，我們所謂的「電微中子」大概就像是黃色——也就是紅色與綠色的「疊加」；至於混合的比例，則取決於混合角(mixing angle)的搭配。

      聽起來可能有些抽象，但用數學式反而更好表達。為了簡潔性，我們在此僅考慮兩種不同味的微中子，對應到的特徵態分別是 $|\nu_e\rangle$ 與 $|\nu_\mu\rangle$，為了解釋微中子振盪、也就是不同「味」特徵態如何「混合」，量子力學的態疊加原理要求引入混合角 $\theta$ 以及對應到質量分別為 $m_1$、$m_2$ 的特徵態 $|\nu_1\rangle$、$|\nu_2\rangle$：

$\being{pmatrix} |\nu_e \rangle \\ |\nu_\mu \rangle \end{pmatrix}= \begin{pmatrix} \cos{\theta} & \sin{\theta} \\ -\sin{\theta} & \cos{\theta} \being{pmatrix} |\nu_1 \rangle \\ |\nu_2 \rangle \end{pmatrix}$

      其中的矩陣在正式文獻中會是 $3 \times 3$ 的，也就是更廣義的 PMNS 矩陣（Pontecorvo–Maki–Nakagawa–Sakata matrix），不過我們在這裡就簡化討論。其實從上面這個式子，我們幾乎就可以總結說微中子振盪意味著它們具有質量了：因為從中可以看出，微中子振盪（也就是 $|\nu_e\rangle$ 與 $|\nu_\mu\rangle$ 的混合）的產生條件源於 $|\nu_1\rangle$、$|\nu_2\rangle$ 的不同，也就是 $m_1 \ne m_2$，這就表示至少有一者質量不為零；否則若 $m_1 = m_2 (= 0)$，即 $|\nu_1\rangle = |\nu_2\rangle$，振盪就不會發生！

      不過為了完整性，我們還是繼續推導下去。考慮 $|\nu_\mu\rangle \to |\nu_e\rangle$ 此一過程，在 $t = 0$ 時 $|\nu_\mu(0)\rangle = -\sin\theta\, |\nu_1\rangle + \cos\theta\, |\nu_2\rangle$，而在時間演化下則有

$|\nu_{\mu}(t)\rangle = -\sin{\theta} e^{-iE_{1}t} |\nu_{1}\rangle + \cos{\theta} e^{-iE_{2}t} |\nu_{2}\rangle$

---

¹如同夸克的例子中，描述「味混合」現象對應到的就是CKM矩陣。

注意：我們在此皆使用自然單位制（$c = \hbar = 1$）。由於微中子以相對論性速度運動（即 $p \gg m$），其中的能量將會是 $E = \sqrt{p^2 + m^2} \simeq p + \frac{m^2}{2p}$。根據量子力學，在一段時間內觀測到微中子從 $|\nu_\mu\rangle$ 轉變成 $|\nu_e\rangle$ 的機率會是：

$P(\nu_{\mu} \rightarrow \nu_{e}) = |\langle\nu_{e}|\nu_{\mu}(t)\rangle|^2$

簡單整理後（$E = p$，外加考量相對論性粒子傳播距離 $L \simeq t$），最後可以得出：

 $P(\nu_{\mu} \rightarrow \nu_{e}) = \sin^2 2\theta \, \sin^2{\left( \frac{\Delta m^2 L}{4E} \right)}$

其中 $\Delta m^2 = m_2^2 - m_1^2$。而上述這就是微中子振盪的重點公式，從中我們可以歸納出幾個重點：

1. 從 $\sin^2\theta$ 等週期函數項能看出，微中子轉變到不同「味」的機率呈週期變化，這也是「振盪」一詞的由來。
2. 除了能量、質量與混合角，微中子振盪的發生機率也與粒子傳播距離 $L$ 有直接關聯。
3. 如果任一微中子質量為零，$\Delta m^2 = 0$，則振盪發生機率為零。微中子振盪的實驗證據，意味著微中子具有非零質量。
4. 我們無法從振盪機率直接推斷微中子的確切質量 $m_1$、$m_2$，只能量測出質量的平方差值 $\Delta m^2$，以及至少其中一者具有非零質量的事實。

在現有的微中子探測實驗中，可控的參數基本上就是能量 $E$ 與距離 $L$，比如筆者所在的美國費米實驗室（Fermilab），其中「短基線微中子計畫」（Short-Baseline Neutrino Program, SBN）就透過三台分別與粒子源有不同距離的探測器，測量微中子振盪。

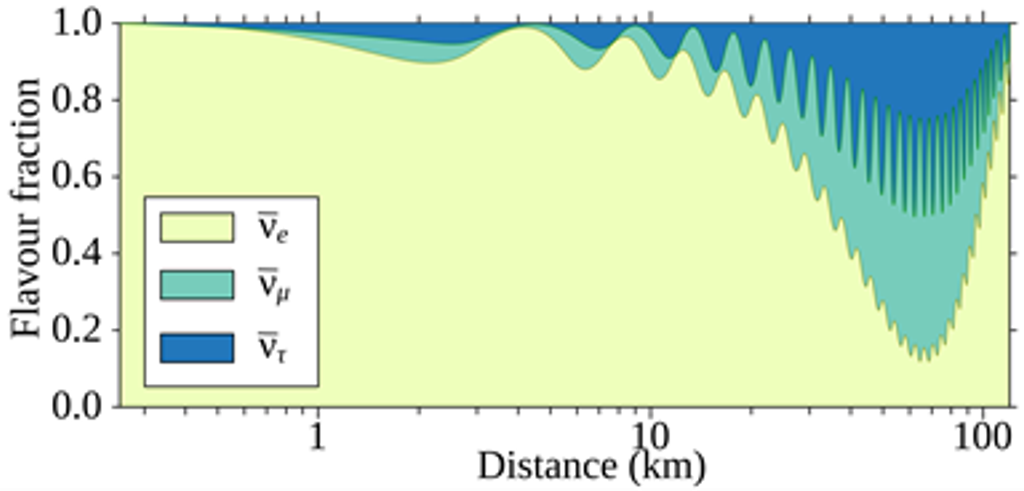
圖5-1: 同樣能級下，三種微中子發生振盪的可能性與傳播距離的關聯。（圖源：Wikipedia）

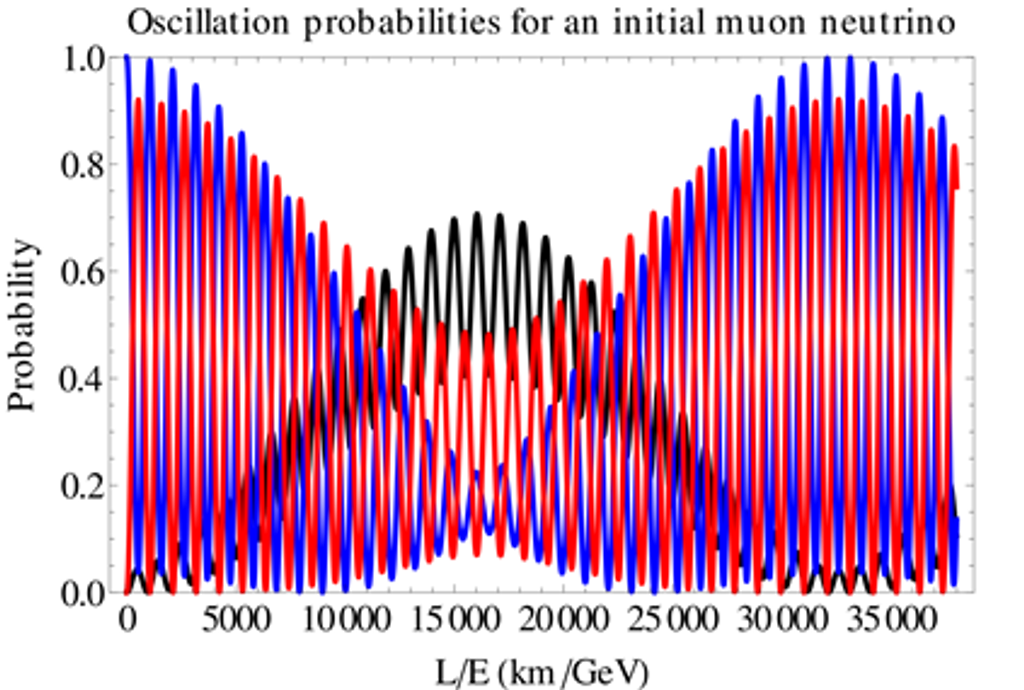
圖5-2: 緲微中子振盪的發生機率與距離-能量比值的關聯：藍色曲線為緲微中子、黑色為電微中子、紅色為淘微中子。由圖中可見，在L/E比值於15,000至20,000左右，緲微中子有最高機率會轉變為電微中子。（圖源：Wikipedia）

 

二、尚未露面——最神秘的「第四種」微中子？

在上一篇探討微中子左右手性（螺旋度）的章節中有提到，我們目前尚未觀測到右手性的微中子。理論上來說，一旦微中子獲得質量，將不可能恆定以光速運動，這使得左、右手性得已被區分開來，意味著必然會觀測到左、右手兩種特徵態。然而，弱交互作用中只有左手性微中子的參與，這就產生了一個矛盾：要不是標準模型錯了、可能就是那些右手性微中子連弱交互作用也不參與！「惰性微中子」(sterile neutrino)就是其中一類右手性微中子。

對於eV級別的惰性微中子，理論上通常會建構擴充版的4x4 PMNS矩陣，也就是所謂的「3+1模型」，亦即把第四種味納入現有的三種微中子框架中 。至於惰性微中子是否存在、是否會參與微中子振盪，這些尚屬目前學術界的活躍領域，諸如上一節提到的SBN計畫等短基線實驗，也會在不久的將來透過更高精度的探測來驗證惰性微中子的可能性。

 

三、插曲：淺談粒子質量、能量與探測難度

值得一提的是，上一段落提到的短基線實驗主要是針對能量落在「eV」等級的惰性微中子、從而驗證「3+1」模型的正確性。那麼還有其他能級的嗎？而這些不同質量、能量對應到的惰性微中子，又會對標準模型產生什麼樣的影響？

首先讓我們複習一下質量與電子伏特（electron volt, eV）的概念。粒子物理學中，電子伏特相當於一顆電子在一伏特電壓下所帶的能量，約為 $1.602 \times 10^{-19}$ 焦耳。質能等價公式（$E = mc^2$）意味著質量與能量是一體兩面的，因此粒子物理學通常會省略常數 $c$，直接將質量用 eV 等單位來表示。電子與原子核之間的能級差約在 eV 尺度，這個能量大約就是將電子彈出原子的大小；假設原子核的束縛能落在 MeV，那麼一旦擁有 MeV 級的能量，就可以拆散原子核。對於日常生活而言，我們可能很難感知這個能量有多強大，畢竟：即使能量高達 $1\ \mathrm{GeV} \simeq 1.602 \times 10^{-10}$ 焦耳，但現實中一顆果子從樹上掉下來的能量大約就是 $1$ 焦耳、將近 $10^{10}\ \mathrm{eV}$（$10\ \mathrm{GeV}$）了——所以我們應該用微觀的角度想：假設一顆蘋果由 $10^{25}$ 個基本粒子所組成，如果每個粒子都擁有 $10\ \mathrm{GeV}$ 的能量，蘋果所攜帶的總能量將高達 $10^{35}\ \mathrm{eV}$，相當於 $10^{16}$ 焦耳——這個能量大概可以撞出直徑一公里的隕石坑了！

---

²只不過MiniBooNE所探測到的低能級過剩(low energy excess, LEE)反常也超出了3+1模型的預期，雖說有可能指向新的振盪模式、但也有可能源於光子與電子訊號的辨別偏誤。

 

      粒子對撞機的概念也是如此，不同的能量等級可以撞出結構更基本的粒子，當然，能量愈大也愈難實現，目前全球最大的對撞機LHC能產生的能量約13.6 TeV (約13,600 GeV)，這個能量雖然對應到的不過是一隻蒼蠅起飛的動能，但在微觀世界中已經是足以模擬早期宇宙的能量級。好消息是，對於eV尺度的惰性微中子，我們並不需要用那麼高能的對撞機去尋找，而是透過「微中子探測器」、藉由微中子與原子或其他粒子的交互作用來推論它們的存在。

      不過，惰性微中子也有可能攜帶更高能量，對於落在keV尺度的惰性微中子，則有可能是「溫暗物質」的候選者。甚至在一些理論中，它們的質量有可能達到更高的能量級，而這也使得我們目前尚未能從微中子探測器中觀測到。

 

四、未解之謎：從惰性微中子到物質起源

      說到微中子質量生成的機制，我們目前所提到的假設都是微中子透過希格斯機制獲取質量，而這類型的微中子屬於「狄拉克費米子」(Dirac fermion)。但其實還有另一種可能性，認為微中子可能是「馬約拉納費米子」(Majorana fermion)，即粒子本身就是反粒子，這種情況下質量則會透過「翹翹板機制」(seesaw mechanism)所獲得 。這種機制可以解釋超重的惰性微中子質量起源：在電弱對稱性發生自發破缺的槓桿上，如果一端的微中子愈輕，另一端惰性微中子的質量就愈重，總之兩者的乘積為一常數。我們目前觀測到的微中子質量幾乎是微乎其微，這就代表了翹翹板機制下的惰性微中子質量將會非常大、約落在低於「GUT能量」的幾個數量級——GUT即大統一理論(Grand Unified Theory)，一旦能量高達1016 GeV，電弱交互作用與強交互作用會變得無法區辨、也就是除重力以外的三種交互作用將被「統一」，我們也相當於能重啟宇宙誕生後

---

³更具體來說，是「第一類」(type I)翹翹板機制。

10^-36 秒時的情景。然而目前實驗尚遠無法達到此能標，而這也是和前述短基線實驗指向的eV能級、或者作為暗物質候選keV能級惰性微中子最大的不同。

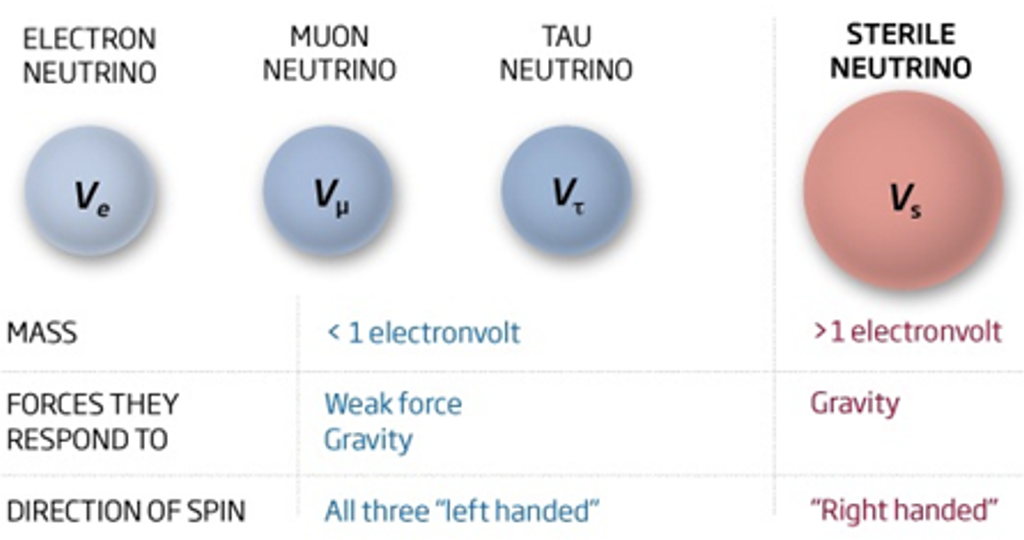圖6-1: 三種微中子與惰性微中子的比較。(圖源: www.quantumdiaries.org/2014/07/27/sterile-neutrinos/)

      此外，高於GeV或TeV尺度的惰性微中子也可以解釋宇宙中粒子多於反粒子的起源。在粒子物理學中，弱交互作用會在一定程度上打破CP對稱性，其中C是電荷共軛（即粒子與反粒子互換）、P是宇稱（鏡像對稱），這就是所謂的「CP破壞」(CP violation)。如今的宇宙幾乎不見反物質的蹤跡、我們也得以存在，這其實是個反常的現象，因為理論上宇宙早期正反物質數量應當是均等的。而根據薩哈洛夫三要件(Sakharov conditions)，CP破壞就是其中一個導因，當正反粒子數量上微小的平衡被打破後，就會像天秤最終徹底往一端傾斜那樣，在正反粒子湮滅的過程中、所剩的粒子以數量略多的優勢主宰了整個宇宙。這一系列過程就是「重子生成機制」(baryogenesis)，而CP破壞至今仍是物理與宇宙學中相當重要的課題。

圖6-2: 我們身在物質主宰的宇宙，但宇宙中物質與反物質的不對稱性仍是未解之謎。（圖源：https://legend-exp.org/science/neutrinoless-bb-decay/the-matter-antimatter-asymetry）

      雖然CP破壞已從夸克的交互作用與CKM矩陣中被證實，但這似乎還不足以解釋宇宙中為何幾乎沒有反物質的存在。換句話說，夸克家族的CP破壞太弱了，無法單獨解釋宇宙中重子不對稱的現象。也因此，人們把目光從夸克移向輕子家族，並嘗試引入了「輕子生成機制」(leptogenesis)。理論上此一機制會發生在重子生成之前：宇宙早期的大質量馬約拉納粒子（如惰性微中子）會先衰變成微中子與輕子，其中正、反輕子數的不對稱將進一步轉化成重子與反重子數目的不對稱，這也能允許較大的CP破壞相位、解釋宇宙中為何幾乎只有物質存在。

      值得注意的是，輕子生成目前尚屬於超越標準模型（BSM）的新物理課題，且由於能量侷限，我們目前自然也無法透過加速器實驗來證實超重惰性微中子的存在。然而，CP 破壞相位 $\delta_{\mathrm{CP}}$ 其實與微中子振盪也有關聯：誠如 CP 破壞的首次驗證來自於夸克的 CKM 矩陣，微中子與輕子家族的 CP 相位本身也是前面提過 PMNS 矩陣中的其中一個參數。在不久的將來，諸如 DUNE（Deep Underground Neutrino Experiment）這類長基線實驗，將有可能探測出 CP 相位 $\delta_{\mathrm{CP}}$ 的精確值，簡單來說就是正反微中子的振盪發生率是否吻合，比如 $P(\nu_\mu \to \nu_e)$ 與 $P(\bar{\nu}_\mu \to \bar{\nu}_e)$ 是否相等，如果相位角夠大則將成為支持輕子生成機制的重要證據之一。

這裡最有意思的地方在於：雖然我們遠遠無法觸及翹翹板機制所描述的能量級，但卻能透過相對可行的微中子振盪來驗證CP破壞、甚至進一步支持諸如大質量惰性微中子這類馬約拉納粒子的存在，而這根本的原因就在於：兩者都源自於湯川耦合的交互作用模型——看似全然不同的兩套理論，其實內在邏輯都是息息相關的。

 

五、結語

微中子作為宇宙中相當古老、也是數量次多的基本粒子，它們無所不在，不僅遍佈了整個空間，也橫越了從宇宙太初時期至今的時間長河，時至今日依然有許多謎團等待科學家們逐一解開。我們也從這兩篇文章中探討了微中子的發現史、探測方法、質量之謎、以及微中子振盪、乃至於與宇宙學的關聯。從微中子振盪被觀測後，人們也意識到這些現象背後似乎也更深層、我們尚未理解的機制存在，這也使得微中子物理在近幾十年來都是粒子物理學的研究前沿。我們也期望在不久後的未來透過新一代探測器，將微中子的謎團、甚至宇宙的神秘面紗逐一揭開。