光譜學(optical spectroscopy)是研究溶液、薄膜和塊材中的化學組成、結構特性與光物質交互作用最廣泛使用的技術之一，根據激發源的頻譜範圍，頻譜學可分類成X-射線光譜學(X-ray spectroscopy)、光譜學(特別在可見光範圍)、電子能譜學(electron spectroscopy)等。X-射線光譜學廣泛應用在探測各種材料的原子局部結構、元素化學組成與電子態，而電子能譜學分析放射或散射電子的能量，能夠辨識元素並確定其電子結構。同時，利用紅外(IR)光源的光譜技術可用來探索分子與固體中的鍵結機制及振動模式(vibrational modes)，因為大部分的分子在電磁光譜的紅外區(4000–400 cm–1)具有特徵的吸收特性，即所謂的分子指紋(molecular fingerprints)，這裡，這些指紋對應特定的電子、振動或自旋態的共振頻率。然而在IR波段以下的低頻範圍，資訊無法由傳統IR光譜學取得，作為代替，一般是利用拉曼散射光譜學(Raman scattering spectroscopy)來探測低能量的振動模式。最近，一種操作於兆赫(terahertz，THz)頻率範圍的新光譜學技術開始興起，提供獨特的機會來表徵材料。如圖1所示，一般可見光源的操作在1015 Hz的數量級，而兆赫波是頻率範圍從幾百GHz (109 Hz)到幾個THz(1012 Hz)的電磁波。值得注意的是，大約在0.1到10 THz的波段 (對應於波長3 mm – 30 μm或3 – 300 cm-1)經常被稱作是「兆赫間隙」(THz gap)，因為這個頻率區間內，傳統電學或光學技術缺乏有效率的光源和適合的偵測器，因此長久以來電磁波的產生和偵測一直備受挑戰。克服這個限制，將驅動能夠操作於THz 範圍的新元件與技術之迫切發展。
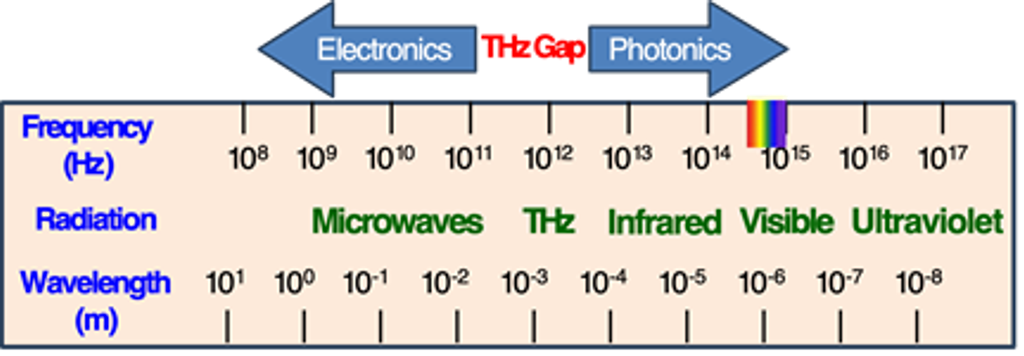圖1、隨著奧斯頓（Auston）開創性地展示以超快雷射脈衝激發的光導天線後，兆赫茲波的產生與量測才得以實現。
隨著雷射技術的重大進展，兆赫波的產生與偵測在超快雷射脈衝激發Auston光導(photoconductive，AP)天線的開創性演示後，變得可行[1]。超快雷射脈衝的脈寬通常在次皮秒（10⁻¹² 秒）等級，並具有極高的峰值功率。這類雷射對於兆赫茲波的產生至關重要，因為它們能在皮秒時間尺度上產生所需的快速變化電流。
過去幾十年已有各種兆赫產生技術之發展，包括光導天線(photoconductive antennas)、非線性晶格電光效應(electro-optic effects)、空氣或氣體電漿產生、量子級聯雷射(quantum cascade lasers)激發量子阱中電子子帶間(intersubband)躍遷，以及基於超穎介面(metasurface)的方法，這些技術可產生連續波或脈衝模式的窄頻或極寬頻兆赫波。1 兆赫茲波的光子能量僅約 4 毫電子伏（meV），比可見光或X光低了數個數量級，這使得兆赫茲成像相較於其他許多成像技術具有顯著的優勢。低的光子能量讓兆赫波能以非侵入性的方式探測電子系統和引發躍遷，將樣品的損害或是擾動減到最小，這讓兆赫波特別適合非破壞性的影像應用，像是機場安檢等。相較之下，高能量的X光與物質之間的交互作用極為強烈，常會導致電離或使材料結構發生改變。
兆赫光譜學另一個獨特優勢在於它的偵測方法。傳統可見光光譜學裡，偵測器只測量光強 $I = |E|^2$，無法得到電場的相位。相較之下，兆赫茲偵測系統可在時間域中直接記錄電場隨時間變化的訊號，常利用光電導天線或電光取樣等方法進行量測。這種直接量測同時保留電場振幅與相位的兩種資訊。這種能力通常被稱為兆赫時域光譜學(THz time-domain spectroscopy，THz-TDS)，容許同時汲取光響應函數如折射率、介電函數、光導率(optical conductivity)等的實部與虛部，而無需借助Kramers–Kronig轉換。除此之外，THz-TDS具有次皮秒的時間解析度，能精確探測超快載子動力學，其直接測定導電率的獨特能力更是傳統光強偵測器無法提供的。
圖2顯示一個典型的 THz-TDS 實驗配置，使用光電導天線同時作為 THz 產生與偵測元件。經緊密聚焦的飛秒雷射（~100 fs）激發發射端 PC 天線，並以拋物面鏡匯聚與整形 THz 光束（一般玻璃透鏡在 THz 區段吸收強，故改用金/銀鍍膜鏡面）。樣品置於 THz 光路中，系統以幫浦–探測延遲掃描量測穿透波形。圖 2(b) 與 2(c) 分別示出時間域 THz 波形，以及經傅立葉轉換得到的頻譜。透過此法，可在頻域中系統性鑑別材料之分子指紋與特徵振動模態。
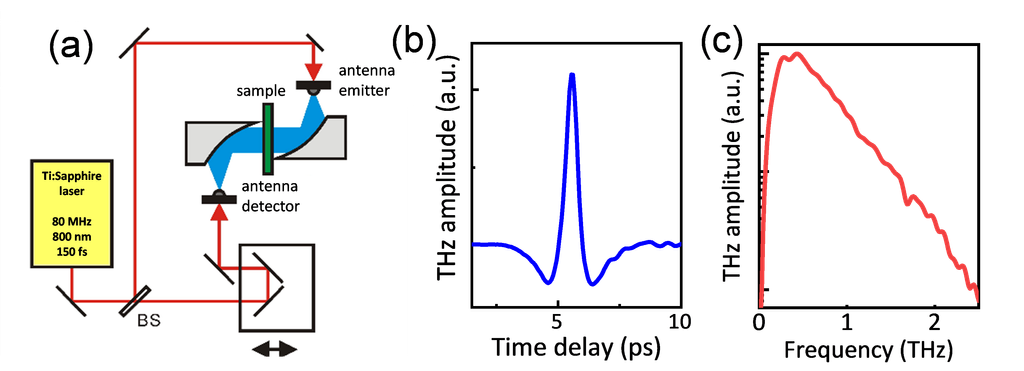圖 2｜兆赫茲時域光譜（THz-TDS）實驗系統。(a) 光電導天線在雷射激發下產生 THz 脈衝；延遲的探測光配合同型 PC 天線進行偵測。拋物面鏡負責集光與準直，樣品置於光路中。(b) 量得的時間域 THz 波形。(c) 對 (b) 波形進行傅立葉轉換所得的 THz 頻譜。
下文將以案例示範利用兆赫光譜學探測鈣鈦礦結構振盪模式以及表徵材料電特性的應用實例。
兆赫光譜學表徵電特性與滲流轉變
對許多難以透過電極接觸且會改變其本徵性質的材料（尤其是奈米結構）而言，能以光學量測取得電性資訊格外珍貴。傳統上，電學特性如載子濃度、遷徙率和導電率常是透過霍爾效應的技術來測量，但這需要電極和特定的樣品幾何，相較之下，THz-TDS提供一種無接觸的非破壞方式探測這些參數，使其成為一個能表徵精細或奈米尺度系統的重要工具。
高透光且具導電性的透明導電電極（TCE）對平面/電漿顯示器與太陽能電池等眾多光電元件至關重要。最常見的 TCE——氧化銦錫（ITO）雖性能良好，但偏脆且成本高，不利於可撓或低成本應用。近年來，銀奈米線（AgNW）薄膜成為具潛力的替代方案：它可用旋轉塗佈或噴塗等簡單室溫製程沉積於幾乎任何基板，同時兼具可撓、透光與低成本等優點。這些薄膜中，奈米線形成高度透明的隨機金屬網路(random metallic network)，然而，隨著奈米線的密度增加，導電率提升卻犧牲了透明度，使這兩種性質之間產生了權衡關係。因此，要同時達到高透明度與高導電率，需仔細地最佳化奈米線的密度，這個平衡由滲流閥值(percolation threshold)的概念所控制，即當奈米線密度 $D$ 在此閥值 $D_c$ 之上，薄膜變為導電性；反之薄膜則維持絕緣 [2]。
利用 THz-TDS，可測量金屬 AgNW 薄膜的複數 THz 導電率，如圖 3(a) 所示。這結果揭示了導電率的實部 $\sigma_r(\omega)$ 隨著頻率持續下降，而虛部 $\sigma_i(\omega)$ 增加，這個頻率相依的行為可用簡單 Drude 模型描述，
$$\sigma(\omega) = \frac{\varepsilon_0 \, \omega_p^2 \, \tau_0}{1 - i \omega \tau_0}$$
其中 $\varepsilon_0$ 為真空介電常數、$\omega_p^2 = \frac{Ne^2}{m^* \varepsilon_0}$ 為電漿頻率、$\tau_0$ 為載子散射時間、$N$ 為載子濃度、$e$ 為基本電荷、而 $m^*$ 為載子的有效質量。值得注意的是，低密度 AgNW 薄膜（$D < D_c$）的複數電導頻譜行為與高密度樣品大不相同，如圖3(b)所示，$\sigma_r(\omega)$ 隨著頻率逐漸增加，而 $\sigma_i(\omega)$ 減少，這不尋常的頻率相依性是如奈米結構的低維材料的典型特徵，可有效地以經驗性 non-Drude 模型（即 Drude–Smith 模型）描述，寫成 [3]
$$\sigma(\omega) = \frac{\varepsilon_0 \, \omega_p^2 \, \tau_0}{1 - i \omega \tau_0} \left[ 1 + \frac{C}{1 - i \omega \tau_0} \right]$$
其中 $C$ 為參數，描述載子在散射後保留原速度方向的比例，範圍介於 $-1$ 與 $0$ 之間。接著，從 Drude–Smith 參數 $C$ 自 $-1$ 到 $0$ 的相變變化，可決定 AgNW 的滲流密度 $D_c$，如圖3(c)所示。插圖描繪當 $D < D_c$ 時電流路徑未連通，換言之，$C$ 值可作為一種評估奈米線網絡連通性的指標。
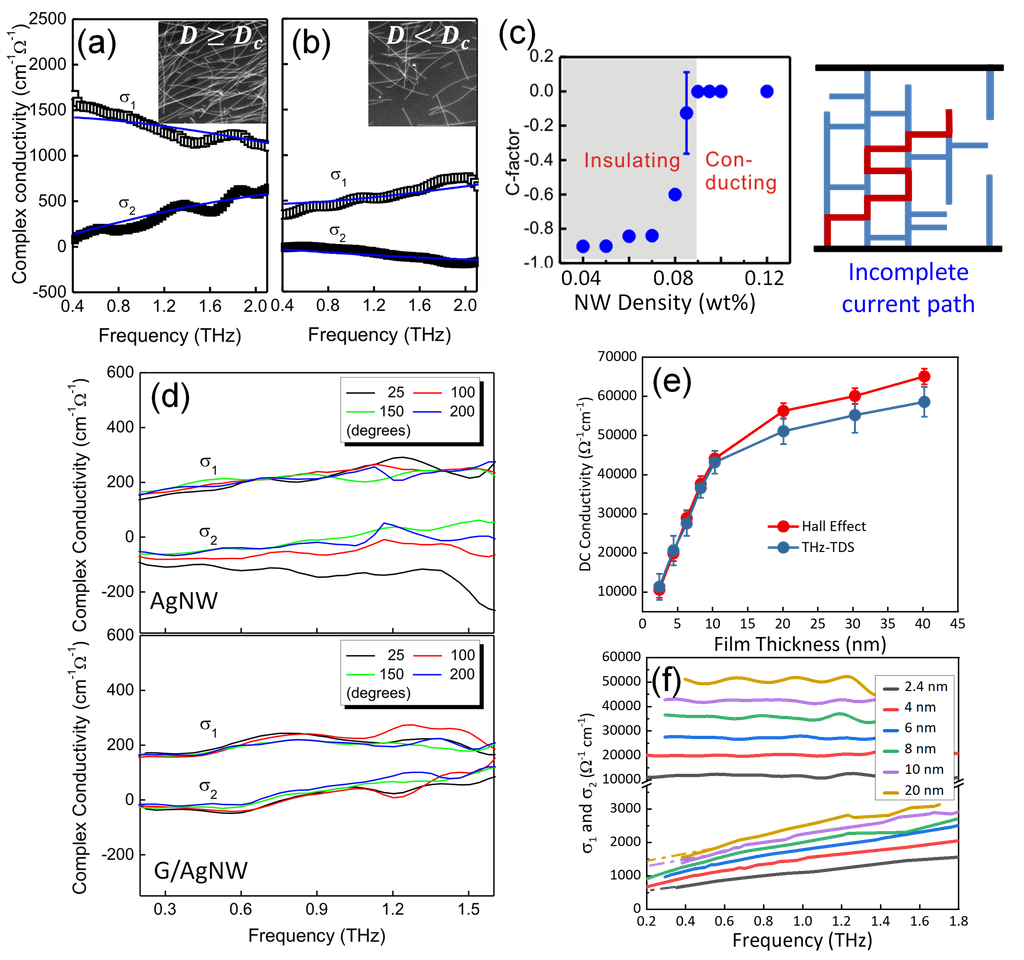圖3、AgNW薄膜的複數導電率對頻率的關係，實線為數據根據(a)簡單Drude與(b) Drude-Smith模型的最佳擬合結果。(c) Drude–Smith C-因子對NW密度的關係，顯示一個清楚的絕緣至金屬的相變。(d) AgNW薄膜與石墨烯覆蓋的AgNW薄膜(GAgNW)在增加退火溫度測量的THz導電性。(e) 以霍爾效應和THz-TDS測量的電導率之比較。(f)厚度小於20 nm的超薄薄膜之複數(包含實部與虛部) THz導電率頻譜。
THz光譜學還能夠研究AgNW網路中的熱引發滲流(thermally induced percolation)與穩定性。網路的高導電率維持到~200 °C，遠低於銀塊的熔點(~960 °C)，當高於200°C，接點(junction)會失效導網路崩潰，造成金屬網路元件的性能損失。石墨烯具有高平面熱導率、穩定性、和可撓性，可緊密黏附在AgNW薄膜上，促進散熱並阻絕空氣與溼氣。如圖3(d)所示，無覆蓋 AgNW 薄膜的 $\sigma(\omega)$ 在 200 °C 附近顯示金屬到絕緣體的相變，而石墨烯覆蓋的 AgNW 薄膜 ($\mathrm{G/AgNW}$) 維持類 Drude 的導電率，展示增強的熱穩定性、電學性能及光學透明度 [4]。
除了奈米金屬線網路外，金屬薄膜在厚度增加時也會發生滲流轉變。貴金屬如金(Au)透過蒸發或濺鍍沉積的過程中，一開始呈現不連續的粗糙形態，一直到厚度超過滲流閥值~6–10 nm，才形成連續的導電薄膜。相比之下，具有岩鹽結構的氮化鈦(TiN)透過分子束磊晶(molecular beam epitaxy ，MBE)成長時，在超薄厚度就能形成平滑連續的薄膜。TiN的滲流厚度可用THz 時域光譜學(THz-TDS)來決定。圖3(e)顯示，霍爾效應與THz-TDS測得的DC電導率相當吻合，和其它方法成長出來的超薄TiN膜成鮮明對比，後者通常在光學與電學測得的電導率有很大的差異。此外，圖3(f)揭示，即使在 $2.4\,\mathrm{nm}$ 的厚度仍呈現金屬的類 Drude $\sigma(\omega)$ 行為，表示 MBE 成長的 TiN 之滲流厚度小於 $2\,\mathrm{nm}$。這些詳細資訊無法透過傳統霍爾效應的技術獲得，證明 THz-TDS 能提供超越霍爾效應測量可得的互補價值。
THz光譜學在理解鈣鈦礦上的角色
幾十年來，矽基太陽能電池因其高效率、穩定性和可擴展性主導了整個光伏(photovoltaic)市場，然而，儘管有這些優點，矽太陽能電池的製程卻涉及複雜且昂貴的過程，而大量研究已經投入尋找擁有可調性質、低成本製造和高功率轉換效率(power conversion efficiencies，PCEs)的新一代材料。混合鹵素鈣鈦礦(hybrid halide perovskites)是目前的研究重點，因為它具備低成本、簡單製程、強光吸收、高載子遷移率等多項優點。如圖4(a)所示，3維有機-無機混合式(organic–inorganic hybrid，OIH)鈣鈦礦具有特定晶格結構ABX3，其中A為小單價有機陽離子(small monovalent organic cation)，B為過渡金屬，X通常為鹵素離子，可由多種化學元素組成，賦予它們高度可調控的光學與電學特性。鈣鈦礦含有BX6結構，有機A陽離子佔據了無機架構內部的空間，最被廣泛研究的是甲基氨基碘化鉛(Methylammonium lead iodide)鈣鈦礦(MAPbI3)，它展現卓越的光學與電學特性，像是寬太陽吸收譜線及高效率電荷傳輸，讓它成為新一代太陽能電池最有希望的候選材料之一。
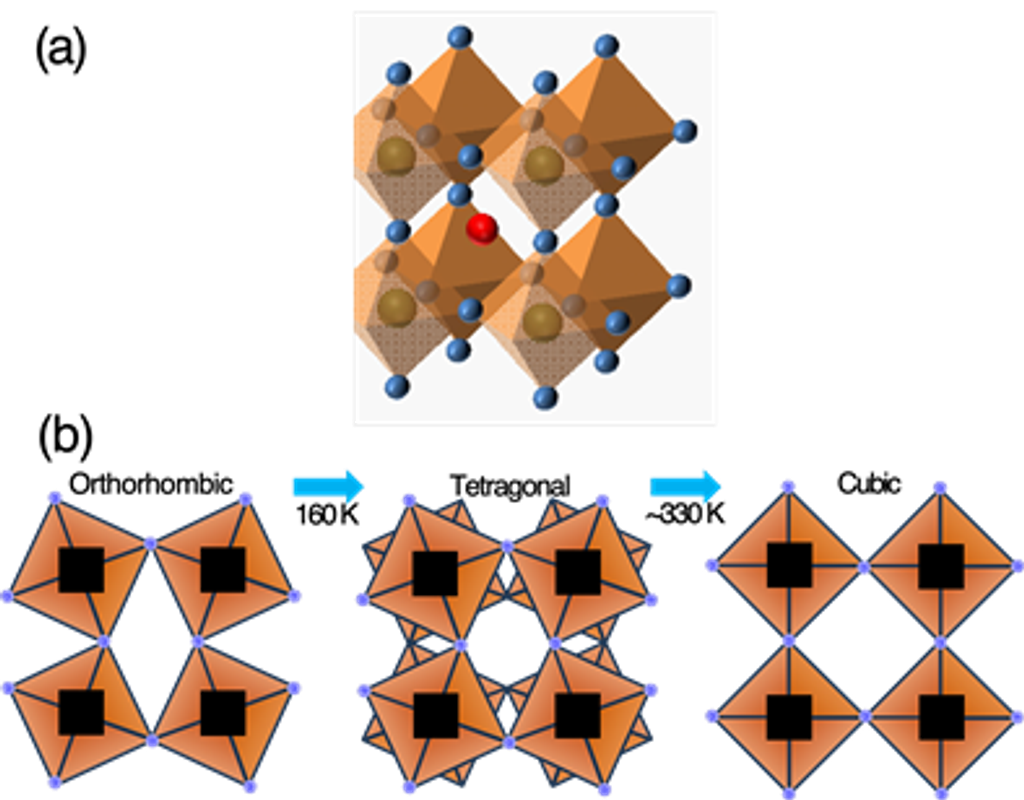圖4、(a)3維有機-無機混合式鈣鈦礦之示意圖。A為小單價有機陽離子，B為過渡金屬，而X為鹵素離子。(b)溫度引發MAPbI3鈣鈦礦的相變，明顯改變八面體結構(octahedral cages)的振動模式。
眾所周知，鈣鈦礦的對稱狀態會隨著溫度改變，圖4(b)中，MAPbI3鈣鈦礦於室溫的相為四方晶系(tetragonal)，當溫度低於160 K時轉變為正交晶系(orthorhombic)[6]。由於八面體架構中的鉛-鹵素成分原子質量較大，特徵振動模式如I–Pb–I彎曲與Pb–I拉伸，一般分別出現在1和2 THz附近。要全面表徵穩定性的不同本質，需結合多種實驗技術，其中紅外/拉曼光譜學常用於了解結構相變與振動模式，但它們的靈敏度在低的頻率範圍(<100 cm-1)大幅下降。因此，0.4到3 THz範圍內擁有高靈敏度的THz-TDS，對表徵鈣鈦礦的聲子模態特別有用處。
圖5(a)和(b)分別為MAPbI3鈣鈦礦的光致發光(photoluminescence，PL)與THz導電率頻譜對溫度的關係，在溫度160 K附近，PL峰值出現約50 nm的突然紅移，同時，低溫下觀察到的兩個清晰THz峰值在1和2 THz附近合併為單一峰值。這些顯著的變化對應MAPbI3鈣鈦礦從正交晶系到四方精細的相變。PL量測與THz光譜學測得的相變溫度一致，表明THz-TDS是檢測鈣鈦礦結構相變的強大技術。
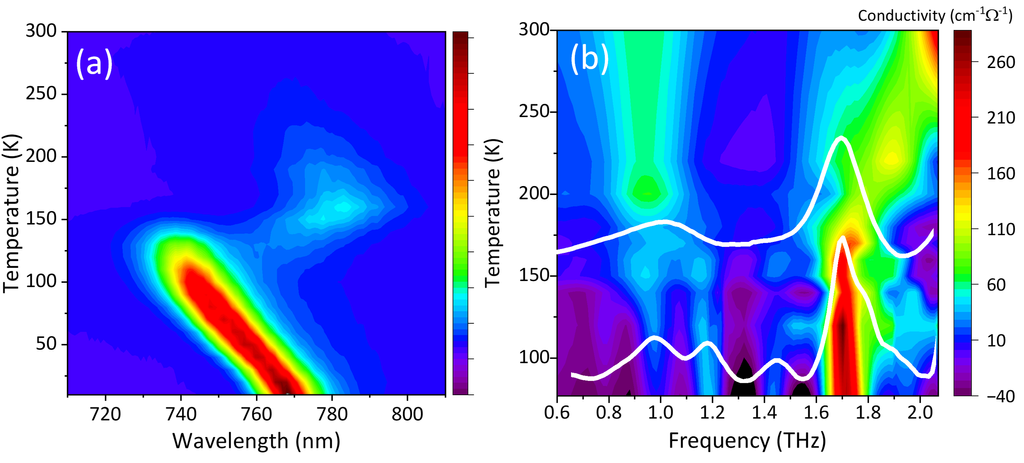圖5、MAPbI3鈣鈦礦的光致發光對溫度相依的等高線圖(a)與THz導電率頻譜(b)。在160 K的臨界溫度附近，PL峰值明顯紅移，並且兩個清晰的THz峰值在~1到2 THz合併為單一峰值。圖(b)中的白色曲線為50和170K測得的THz導電率。
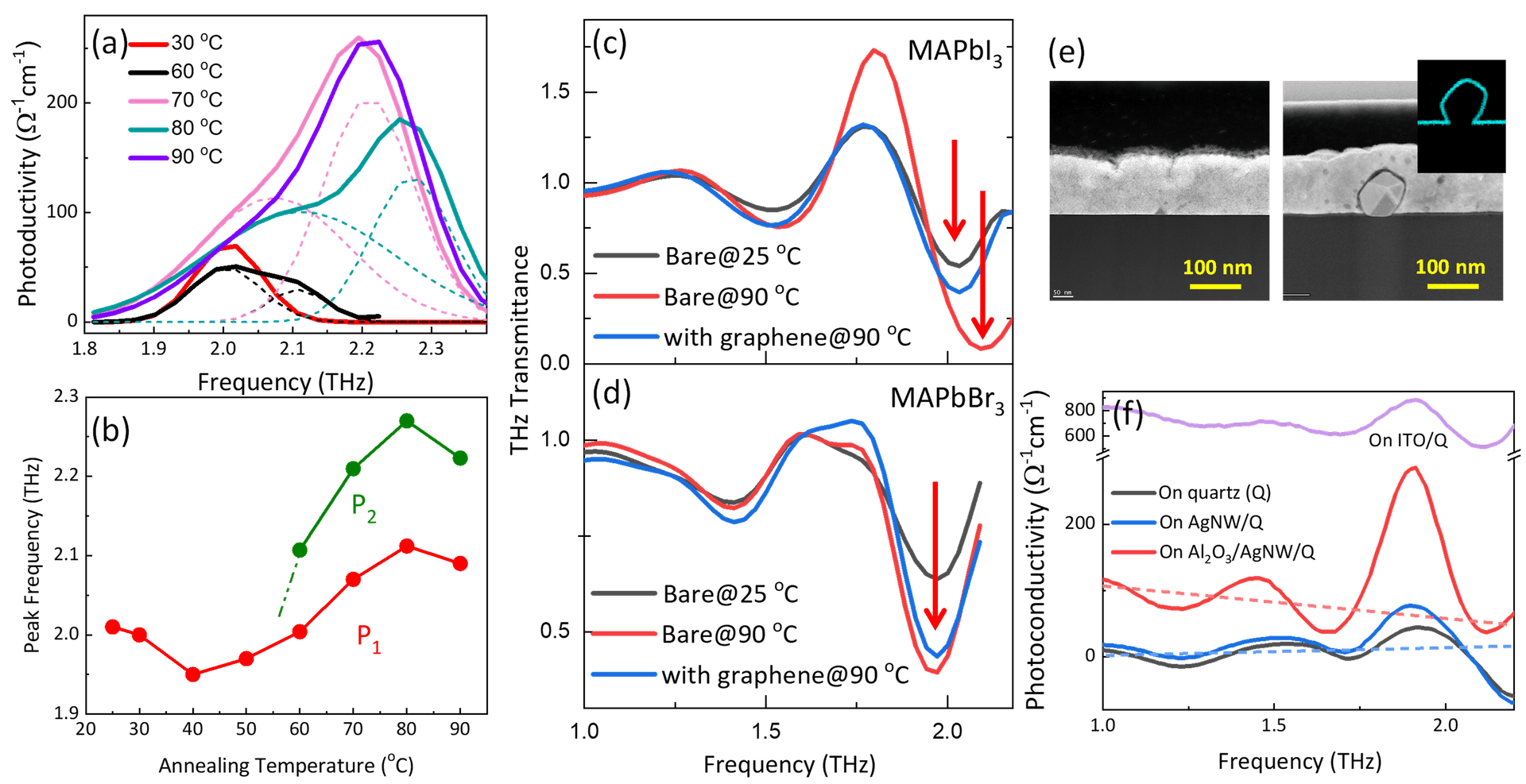
但同時，MAPbI3因各種內在和環境因素導致的嚴重不穩定性，引發人們對實際元件效能的質疑。除此之外，對於在戶外長期接受太陽輻射的太陽能電池，不斷加熱也可能會導致熱不穩定性，這個問題在基於MAPbI₃的太陽能電池中特別關鍵，因為MAPbI₃在約60–65 °C會經歷另一種從四方晶系到立方晶系的結構相變，這溫度明顯低於太陽能電池一般最高的操作溫度(~85 °C)。因溫度引起相變導致的PbI6架構扭曲，直接造成元件的熱不穩定性。圖6(a)為MAPbI₃薄膜隨溫度從室溫增加到90 °C的THz 導電率，當溫度小於60 ℃，為一中心於2 THz的單一峰值，但到了60 ℃，在2.1 THz處出現一個新的小峰[7]。圖6(b)中，峰值的分離變得更加明顯，並且溫度的進一步增加，導致峰值向更高頻率的更大位移。這和MAPbI3在~160 K的模式分裂類似，但後者是歸因於正交晶系到四方晶系的相變。
為了解決升高溫度所產生的熱不穩定性問題，我們引進石墨烯覆蓋層，其水平面與垂直面方向之間的熱流異向性超過100倍。圖6(c)為MAPbI₃的THz穿透(transmittance)光譜，對於MAPbI₃，當在90 °C退火時，因為相變，接近2 THz的峰值移動到更高的頻率，而具石墨烯覆蓋層的樣品並無顯示此位移。為驗證這個觀察，我們在另一種室溫下以立方相存在的OIH鈣鈦礦MAPbBr3進行相同的量測。圖6(d)顯示，即使模式強度增加，在退火過程並中未偵測到MAPbBr3 THz穿透光譜的頻率位移，證實石墨烯覆蓋層能有效鈍化鈣鈦礦太陽能電池的熱。
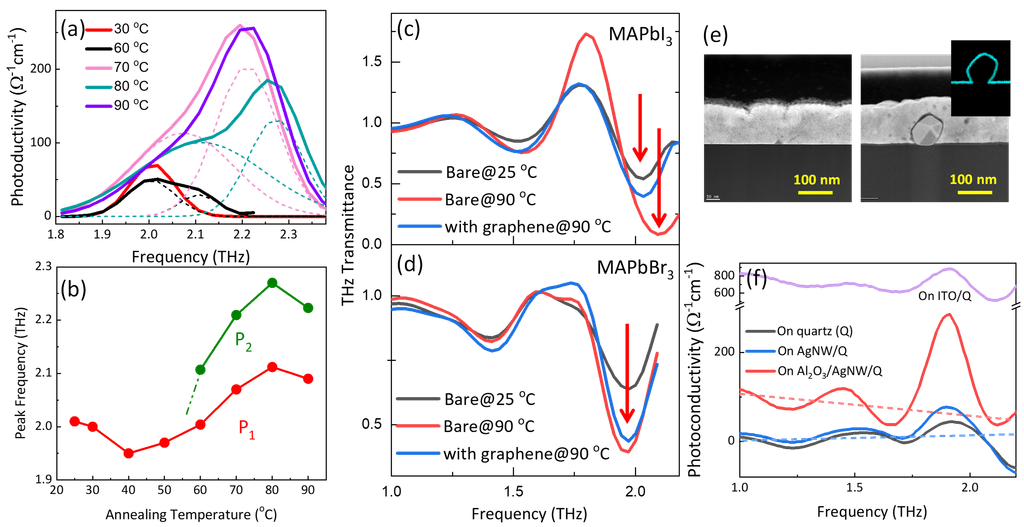圖6、(a) ~2 THz共振聲子模態的光導率(photoconductivity)頻譜與峰值擬合曲線。(b)分離峰值於不同退火溫度的頻率位移。(c)(d) 分別為MAPbI3與MAPbBr3在有、無石墨烯覆蓋層下於25 和 90 ℃的THz穿透率。(e) MAPbI3/AgNW 和 MAPbI3在石英基板上的橫截面(Cross-sectional)TEM影像，插圖為鋁(Al)元素的X射線能量色散光譜(energy-dispersive spectroscopy mapping，EDS mapping)。(f) MAPbI3於石英、AgNW及AgNW上的光導率頻譜，以及AgNW於導體氧化物―銦 錫氧化物上的光導率頻譜。
同時，在垂直整合的複合元件中，不同組件之間的接觸介面也可能會產生關鍵的不穩定性，特別是，太陽能電池中的透明導電電極(TCE)直接接觸鈣鈦礦層，其在介面的穩定性對決定元件的效能至關重要。在前面章節，我們證明AgNW網路是卓越的TCE材料，然而，對於AgNW網路層上的MAPbI3 (MAPbI3/AgNW)，銀原子和碘離子之間的化學反應不僅嚴重損害鈣鈦礦層，也降低系統的導電率。近年來的大量研究發現，插入薄金屬氧化層(例如：Al2O3)可以有效防止相鄰層之間的離子擴散與化學反應。圖6(e)展示了MAPbI3/AgNW的穿隧電子顯微鏡(TEM)影像，在覆蓋至少10 μm區域的TEM影像中(遠大於NWs間的平均空隙≤5 μm)，未發現AgNW，這可能歸因於未受到保護的AgNWs發生分解。相比之下，對於MAPbI3/Al2O3/AgNW，可清楚觀察到被鈣鈦礦層覆蓋的5邊形AgNW，此外，插圖展示Al元素的能量色散X射線光譜圖，其完全沿著AgNW的輪廓分布，證實超薄Al₂O₃中間層共形覆蓋了AgNW的表面。接下來，我們利用THz-TDS方法測量MAPbI3合併 AgNW 底部電極的 $\sigma_1(\omega)$，，有趣的是，圖6(f)顯示，當未受保護的AgNWs合併MAPbI3，MAPbI3/AgNW的THz響應與石英基板上的單層MAPbI3幾乎相同，表示在MAPbI3層沉積後，AgNW網路的連續導電路徑消失。MAPbI3/石英與MAPbI3/AgNW之間觀察到的類似響應，表明在溶解過程中，鈣鈦礦可能滲入AgNWs的間隙並與Ag原子作用，導致AgNW網路的滲流路徑斷開。同時，對於MAPbI3/Al2O3/AgNW，$\sigma_1(\omega)$ 表現出明顯的類 Drude 頻率相依性，其 DC 導電率遠高於 MAPbI$_3$/AgNW。
兆赫光譜學已成為一個探測材料基本特性的強力工具，透過直接存取所謂THz間隙頻率範圍的低能量激發與聲子模態，它揭示傳統電學或光學技術一般無法得到的見解。本文中，筆者經由幾個範例研究，證明THz光譜學對導電率、振動指紋及結構相變具有高靈敏度，對研究新興材料像是鈣鈦礦、奈米結構、超薄金屬膜等特別有用。除此之外，兆赫時域光譜學能夠實現無接觸、非破壞及空間解析的電學特性量測，補足霍爾效應等傳統方法。總而言之，這些能力不但讓THz光譜學成為了解材料特性的基本研究工具，亦有望成為指引次世代光電與能源元件設計與最佳化的關鍵技術。
參考文獻:
[1]D. H. Auston, K. P. Cheung, and P. R. Smith, Picosecond photoconducting Hertzian dipoles, Appl. Phys. Lett., 45, 284-286 (1984).
[2]Y.-J. Tsai, C.-Y. Chang, Y.-C. Lai, P.-C. Yu, and H. Ahn, Realization of metal−insulator transition and oxidation in silver nanowire percolating networks by terahertz reflection spectroscopy, ACS Appl. Mater. Interfaces 6, 630 (2014).
[3]N.V. Smith, Classical generalization of the Drude formula for the optical conductivity Phys. Rev. B, 64, 155106–4 (2001).
[4]J.-Z. Chen, H. Ahn, S.-C. Yen, and Y.-J. Tsai, “Thermally induced percolational transition and thermal stability of silver nanowire networks studied by THz spectroscopy,” ACS Appl. Mater. Interfaces, 6, 20994 (2014).
[5]I Hong Ho, C.-W. Chang, Y.-L. Chen, W.-Y. Chang, T.-J. Kuo, Y.-J. Lu, S. Gwo, and H. Ahn, Ultrathin TiN epitaxial films as transparent conductive electrodes, ACS Appl. Mater. Interfaces. 14, 16839–16845 (2022).
[6]Whitfield, P., Herron, N., Guise, W. et al. Structures, phase transitions and tricritical behavior of the hybrid perovskite methyl ammonium lead iodide. Sci Rep 6, 35685 (2016).
[7]Z.-W. Huang, Y.-H. Hong, Y.-J. Du, T.-J. Kuo, C.-C. Huang, T. S. Kao, and H. Ahn, THz analysis of CH3NH3PbI3 perovskites associated with graphene and silver nanowire electrodes, ACS Appl. Mater. Interfaces. 13, 9224–9231 (2021).
