自1960年代起，超導技術已成功應用於 SQUID 磁通感測器與高靈敏度的光子/輻射感測器，展現出超導電路在精密量測上的獨特優勢。進入1980年代後，隨著一系列關鍵實驗逐步證實巨觀尺度下的量子行為可在超導電路中被操控與量測，超導系統不再僅被視為經典電子元件，更是成為可用於探索與應用量子力學的實體平台。這些奠基性的成果，推動了量子資訊科學的快速發展，亦在去年的諾貝爾物理獎中獲得高度肯定。

在此背景下，超導量子電腦逐漸成為實現可擴展量子運算的主要路線之一。本文將從超導電路的量子特性出發，介紹超導量子位元與其運作原理，並探討超導量子電腦在發展過程中所面臨的關鍵挑戰與未來方向。

超導電路的量子性

1957 年，John Bardeen、Leon Cooper 與 John Schrieffer 提出著名的 BCS 理論，從微觀角度說明超導態源於電子透過晶格振動形成庫珀對 (Cooper pairs)，並集體凝聚於同一量子基態，展現長程相位同調的巨觀量子行為[1]。這一理論奠定了理解傳統超導體量子性質的基礎。在此基礎上，Brian Josephson 於 1962 年預測，在兩個超導體之間夾有一層極薄的絕緣層，超導態的波函數仍可延伸穿越此能障，使電流在無電壓降的情況下流動[2]。此結構被稱為約瑟夫森接面 (Josephson junction)。此超導電流 $I$ 與兩側超導體波函數的相位差 $\delta \equiv \delta_2 - \delta_1$ 之間關係，可由第一約瑟夫森關係式描述：

$$I = I_0 \sin \delta$$                                                                                                         (1)

其中 $I_0$ 是約瑟夫森接面的臨界電流。當接面上存在電壓降 $V$ 時，超導相位差會隨時間演化，其動力學行為可由第二約瑟夫森關係式描述：$\frac{d\delta}{dt} = \frac{2e}{\hbar}V$。

$$V = \frac{\Phi_0}{2\pi} \dot{\delta}$$                                                                                    (2)

其中 $\Phi_0 \equiv h/2e$ 為磁通量量子、$h$ 為普朗克常數、$e$ 為電子電荷量。這兩個約瑟夫森關係式揭示了超導相位差與電流、電壓之間的量子關聯性，使約瑟夫森接面成為一種可將量子相位直接轉換為可觀測電路物理量的非線性量子元件，並奠定超導量子電路的核心物理基礎。

這項理論預測隔年由貝爾實驗室的Philip Anderson與John Rowell實驗驗證[3]，確立了約瑟夫森效應的物理實在性。物理學家進一步發現，將兩個約瑟夫森接面構成超導閉合環路，可形成超導量子干涉元件（SQUID，Superconducting Quantum Interference Device），其能承載的超導電流會隨穿過環路的磁通量呈現週期性變化。此一量子干涉效應使SQUID成為目前最靈敏的磁場感測器之一，並廣泛應用於基礎研究與精密量測領域。

1970 年代末期，Anthony Leggett 提出著名的問題，量子力學是否同樣適用於巨觀系統？他進一步指出，約瑟夫森接面所構成的超導電路，因其具備可調控的非線性與低耗散特性，是檢驗巨觀量子行為的理想實驗平台，特別可用來觀測量子穿隧效應[4]。在此脈絡下，John Clarke、Michel Devoret 與 John Martinis 三人合作，於 1980 年代，利用以約瑟夫森接面為核心的超導電路（如圖一(a)）進行一系列實驗，成功驗證巨觀量子現象的存在。此類系統可由 RCSJ (Resistively and Capacitively Shunted Junction) 模型加以描述，如圖一(b) 所示，一個具有臨界電流 $I_0$ 的約瑟夫森接面，並聯描述損耗的等效電阻 $R$ 及三明治結構所形成的等效電容 $C$，並施加外部電流偏壓 $I$。根據科希荷夫電流定律與前述兩個約瑟夫森關係式（式(1)、(2)），可得到接面相位差 $\delta$ 的運動方程式：

$$I = \frac{\hbar C}{2e}\ddot{\delta} + \frac{\hbar}{2eR}\dot{\delta} + I_0 \sin\delta$$                                            (3)

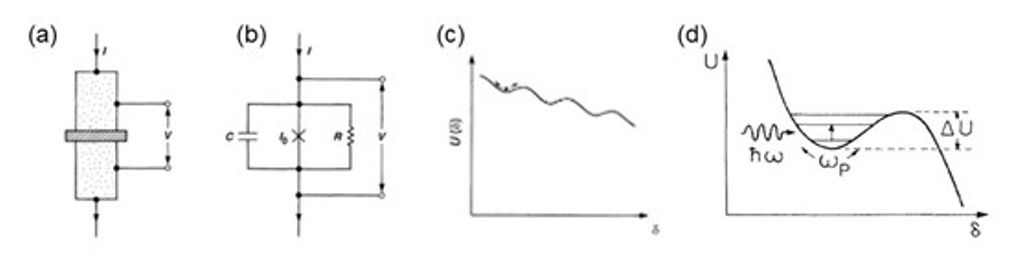
圖一：約瑟夫森接面的 RCSJ (Resistively and Capacitively Shunted Junction) 等效電路模型[6,39]。(a) 約瑟夫森接面電路示意圖。(b) RCSJ 等效電路，包含具臨界電流 $I_0$ 的約瑟夫森接面、並聯電阻 $R$、電容 $C$，以及外加電流偏壓 $I$。(c) RCSJ 模型對應的傾斜洗衣板位能隨相位差 $\delta$ 作圖。當電流偏壓 $I < I_0$ 時，相位粒子侷限於局部位能井中，系統處於超導無電壓降狀態 ($V = 0$)。(d) 局部位能井示意圖。相位粒子可透過熱激發或量子穿隧效應逸出位能井，進入具有電壓降狀態。位能井量子化後形成離散能階，圖中示意由頻率為 $\omega/2\pi$ 的光子誘發，相位粒子由基態躍遷至第一激發態。（圖(a)-(c) 取自參考文獻[39]，圖(d) 取自參考文獻[6]）

其中 $\hbar \equiv h/2\pi$。此方程式等效於描述一個具質量與阻尼的粒子在一維位能中的運動，該等效粒子被稱為相位粒子。其感受到的位能可寫為：

$$U(\delta) = -\frac{\hbar I_0}{2e} \cos\delta - \frac{\hbar I}{2e} \delta$$                                                    (4)

此位能形狀類似一個傾斜洗衣板，如圖一(c) 所示。當 $I < I_0$ 時，相位粒子被侷限於局部位能井中，電路處於超導狀態（無電壓降），此表現與約瑟夫森效應預期一致。隨著 $I$ 接近 $I_0$，位能屏障高度逐漸降低。在有限溫度下，當位能屏障高度與環境熱擾動相當時，相位粒子可藉由熱激發跨越位能屏障，使電路由超導態切換至具有電壓降的狀態。此切換率隨溫度下降而減小，符合波茲曼統計預期[5]。然而，在極低溫下，實驗觀察到切換率隨溫度下降呈飽和表現，揭示相位粒子透過量子穿隧效應穿越位能屏障[5]。

此外，當電路處於上述束縛態時，相位粒子會在局部位能井中進行小振幅振盪，如圖一(d) 所示，其振盪頻率由約瑟夫森接面所表現出的非線性電感，及其三明治結構所形成的等效電容共同決定，整體行為可視為一個非線性 LC 振盪器。對此電路施加微波輻射，實驗上可觀察到在特定偏壓電流 $I$ 下，電路由超導態切換至電壓態的機率明顯增加[6]。此現象發生於微波頻率所對應的光子能量，恰好與電路中基態與激發態之間的能量差相符，表示電路可吸收微波光子躍遷至激發態，進而更容易跨越位能屏障。這類微波誘發躍遷實驗，進一步確認超導電路中能階具有離散量子化結構[6]。John Clarke、Michel Devoret 與 John Martinis 三位物理學家這一系列實驗成果，首次在無歧義的情況下證實，即使是由大量電子組成、具備巨觀自由度的超導電路系統，仍嚴格遵循量子力學的描述。三人相關工作是巨觀量子現象與量子工程領域的里程碑，在去年獲得諾貝爾物理獎的肯定。這些結果不僅為超導量子位元的實現奠定了關鍵實驗基礎，也確立了電路量子化 (circuit quantization) 的物理實在性。在電路量子化的框架下，電荷量 $q$ 與節點磁通量 $\phi$ 構成一對共軛觀察量，完全類比於量子力學中的位置與動量。並且約瑟夫森接面所提供的強非線性電感，以及 SQUID 結構中可透過外加磁通調控的有效電感，至今仍是各類超導量子位元中不可或缺的核心元件。

超導量子電腦發展

量子電腦的概念可追溯至Richard Feynman於 1980 年代初期所提出的洞見，由於自然界本身遵循量子力學，以量子系統來模擬物理系統，有望有效解決古典電腦難以處理的物理問題[7]。此一構想奠定了量子計算的理論動機。隨後，Peter Shor於 1994 年提出可在通用量子電腦上有效率執行質因數分解的演算法[8]，顯示量子電腦在特定計算任務上具備指數級差異的潛在優勢，是量子計算從概念性研究邁向實用性探索的重要里程碑。

眾多量子位元實現平台中，超導電路迅速成為備受矚目的候選方案。其關鍵優勢在於超導電路可利用微影與薄膜沉積等成熟製程製作，與現代積體電路工藝高度相容，且電路拓撲及參數與具有高度可設計性，為大規模系統擴展提供可行路徑。儘管超導量子電路需在極低溫環境下運作，典型工作溫度約為0.02 K絕對溫度，這一技術門檻並未阻擋其快速發展，反而促成低溫工程與量子控制技術的同步進步。1999年，Yasunobu Nakamura、Yuri Pashkin與Jaw-Shen Tsai首次在超導電路中，於不同電荷數狀態之間實現可觀測的量子相干振盪[9]，成功展現量子態的相干控制。這項突破性實驗標誌著第一個超導量子位元，電荷量子位元（charge qubit）的誕生，同時也是首個在固態系統中實現的量子位元，正式揭開超導量子計算研究的序幕。

物理學家陸續提出多種不同型態的超導量子位元設計，如磁通量子位元（flux qubit）與相位量子位元（phase qubit），各自於可操控性、相干時間與可量測讀取性上展現不同優勢與限制[10]，推動了超導量子電路在設計與控制技術上的快速演進。2004 年，電路量子電動力學（circuit quantum electrodynamics）架構被提出[11]，將超導量子位元與高品質因子的線性微波共振器耦合，形成可控的光與物質交互作用系統。隨後的實驗結果顯示，量子位元與共振器之間的能量交換速率可大於系統的耗散率，系統進入強耦合範疇（strong coupling regime）[12]。微波共振器也首次被利用作為量子位元狀態的量測讀取元件，達到量子態的非破壞性讀取，奠定了目前超導量子位元讀取技術的基本架構。2007年提出的 transmon 量子位元設計[13] ，透過提高約瑟夫森能量與電荷能量之比值，大幅抑制電荷雜訊對量子位元的影響，顯著延長相干時間，同時仍保有足夠的非線性以實現量子控制。由於其電路結構相對簡單、製程成熟、且易於透過電容或共振腔進行耦合，transmon 量子位元逐漸成為發展可擴展超導量子處理器的主流選擇，被多數超導量子電腦平台採用。

在超導量子電路的材料選擇上，長期以來主要採用鋁（Aluminum）與鈮（Niobium）等傳統超導金屬。其中鋁因其表面可在常溫、純氧環境下自然形成品質穩定的氧化鋁（AlOx）薄層，成為製作高品質約瑟夫森接面的首選材料。此製程成熟、可重現性高，是目前多數超導量子位元的標準作法。相較之下，鈮具有較高的臨界溫度與臨界磁場，早期常用於微波共振腔與超導電路佈線，但其氧化層品質與介面損耗較難精準控制，使其在接面品質與相干時間上存在一定挑戰。近年來，鉭（Tantalum）逐漸受到重視。實驗顯示，以鉭製作的電容與量子位元，可顯著降低介面損耗，並展現出優異的能量弛豫時間T_1表現[14]。這一發現突顯材料科學在提升超導量子位元相干性上的關鍵角色，也促使研究重心從單純的電路設計，進一步延伸至材料純度、薄膜結構與介面工程的系統性優化。

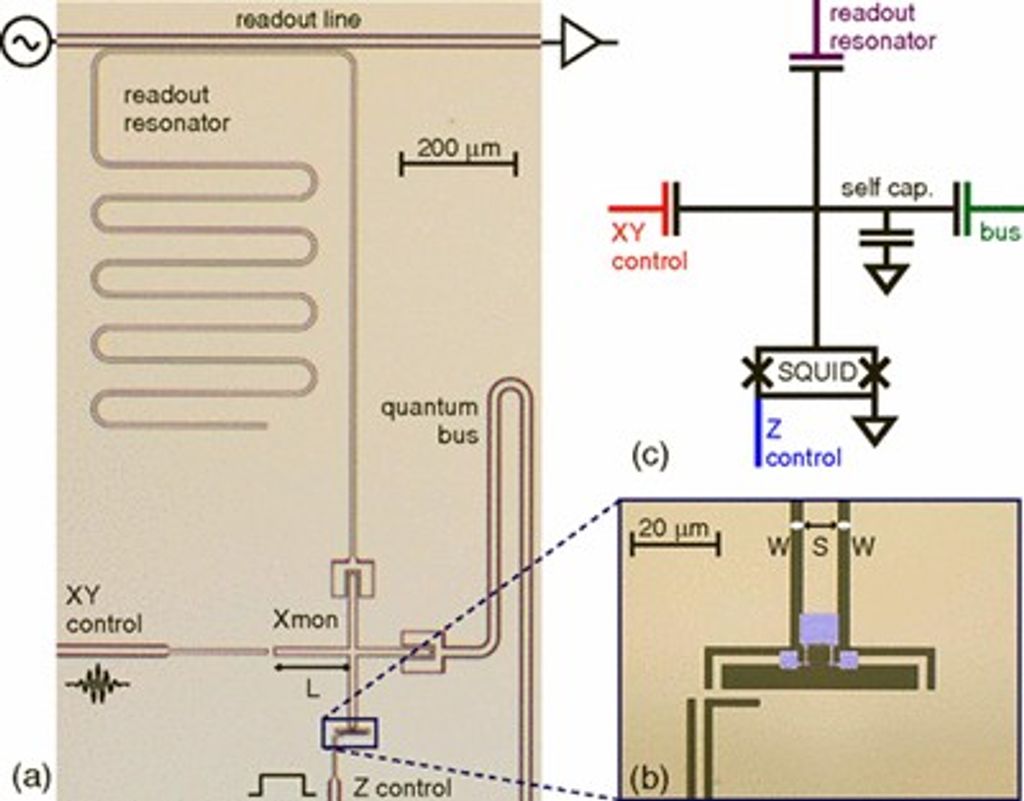
圖二：超導量子位元基本結構[15]。(a)電路佈局照片。中間十字結構搭配下方連接的SQUID形成頻率可調的量子位元。量子位元上方的1/4波長振盪器為量子位元讀取元件。左方傳輸線做為x-y單位元邏輯閘訊號輸入埠。下方傳輸線做為z單位元邏輯閘訊號輸入埠。右方經由傳輸線振盪器與其他量子位元耦合。(b) SQUID放大近照。(c)電路簡圖。（圖取自參考文獻[15]）

圖二(a)、(c) 展示典型 transmon 量子位元的基本架構[15]。中央的十字形金屬結構與周圍接地金屬共同形成電容，其典型尺寸約為數百微米，而十字下方所連接的 SQUID 則提供可調的非線性電感。兩者結合後構成一個頻率可調的非線性振盪器，其能譜中最低的兩個能階被選作量子位元的邏輯態 $|0\rangle$ 與 $|1\rangle$。量子位元的工作頻率由 $|0\rangle$ 與 $|1\rangle$ 之間的能量差除以普朗克常數 $h$ 決定，通常選擇在 5 GHz 左右。此頻率所對應的能量尺度，明顯高於稀釋製冷機所提供之極低溫環境（約 0.02 K）下的熱擾動能量，使量子位元較不易受到熱激發影響；同時，該頻段的微波元件與控制電子設備相對成熟且成本可控，因而成為目前超導量子電腦的主流選擇。

在量子位元的上方，十字結構透過電容與一個四分之一波長微波共振器耦合。此共振器與量子位元的頻率差遠大於其耦合強度，使系統運作於色散（dispersive）耦合區間。該共振器負責量子位元狀態的讀取，當接近共振器頻率的微波脈衝通過系統被散射後，其相位或振幅將攜帶量子位元狀態的資訊。在十字結構左側，量子位元透過電容與一條傳輸線耦合，與量子位元頻率相近的微波脈衝可由此送入，藉由調控脈衝的強度、相位與持續時間，可實現 $|0\rangle$ 與 $|1\rangle$ 間的相干轉換，對應於 $x$ 與 $y$ 軸方向的單位元邏輯閘。下方的 SQUID 可經由與另一條傳輸線的互感耦合（見圖二(b)），注入電流脈衝以改變穿過 SQUID 的磁通量，進而調整量子位元頻率。此頻率調控對應於 $z$ 軸方向的單位元邏輯閘操作。在右側，量子位元可透過電容耦合、共振腔傳遞、或可調耦合器 (tunable coupler) 等方式，與其他量子位元連結，進行雙位元邏輯閘。其中可調耦合器的優勢在於能完全關閉量子位元之間的耦合，對於提升邏輯閘的保真度至關重要。

在雙量子位元耦合機制確立、且具備足夠控制與讀取線路的條件下，量子位元數目便可依相同架構持續擴充。超導電路中第一個雙位元邏輯閘與量子糾纏實驗於2003年實現[16]。經過二十餘年的技術累積與工程化發展，目前已能實作包含百個以上量子位元的超導量子處理器，標誌著超導量子電腦邁入可擴展系統的階段。

近年來，多家科技巨擘與新創公司相繼投入超導量子電腦的研發，使此領域進展顯著。大型科技公司如IBM、Google與Fujitsu，持續在超導量子處理器與系統整合方面進行長期投資。同時也有多家新創公司專注於以超導電路為核心的量子計算技術，例如Rigetti與IQM。此外，D-Wave則以超導電路實現量子退火（quantum annealing）系統聞名，雖其計算模型不同於通用型（閘式）量子電腦，仍在特定最佳化問題上展現獨特應用潛力。在這些努力之下，超導量子電腦在系統層級整合方面已取得領先地位，涵蓋多量子位元晶片、低溫控制、微波操控與即時讀取等關鍵技術。其中，Google於 2019 年發表的實驗成果，首次宣稱達成量子霸權（quantum supremacy）[17]，在特定隨機量子電路取樣任務上，其超導量子處理器完成的計算量，被認為在當時已超出古典超級電腦於合理時間內可達成的範圍。此一結果隨後也引發廣泛討論。後續研究顯示，透過改進古典演算法與高效能運算資源，該任務在古典電腦上仍可於合理時間內完成，這些回應本身亦推動了古典演算方法的顯著進步。但更重要的是，在不同計算任務與實驗設定中，量子優勢（quantum advantage）或量子霸權的展示仍陸續出現，顯示量子硬體在特定問題類型上，已逐步展現超越傳統計算架構的潛力。

然而，量子位元不可避免地會與周遭環境交互作用，導致相干性喪失與操作錯誤。在此情況下，若要實現真正通用型量子電腦，執行具實用價值的長深度量子演算法，量子邏輯閘的錯誤率必須被壓到極低水準。根據不同演算法與容錯架構的估計，所需的邏輯錯誤率通常需低於約10^-12至10^-16，遠低於目前單一超導量子位元可直接達成的10^-3水準。因此，量子糾錯（quantum error correction，QEC）成為通往實用量子計算不可或缺的關鍵技術。其核心概念是利用多個實質量子位元（physical qubits），以糾錯碼的形式共同編碼一個用於運算的邏輯量子位元（logical qubit），並透過持續狀態讀取與解碼來偵測與修正錯誤，從而將邏輯量子位元的有效錯誤率大幅降低。

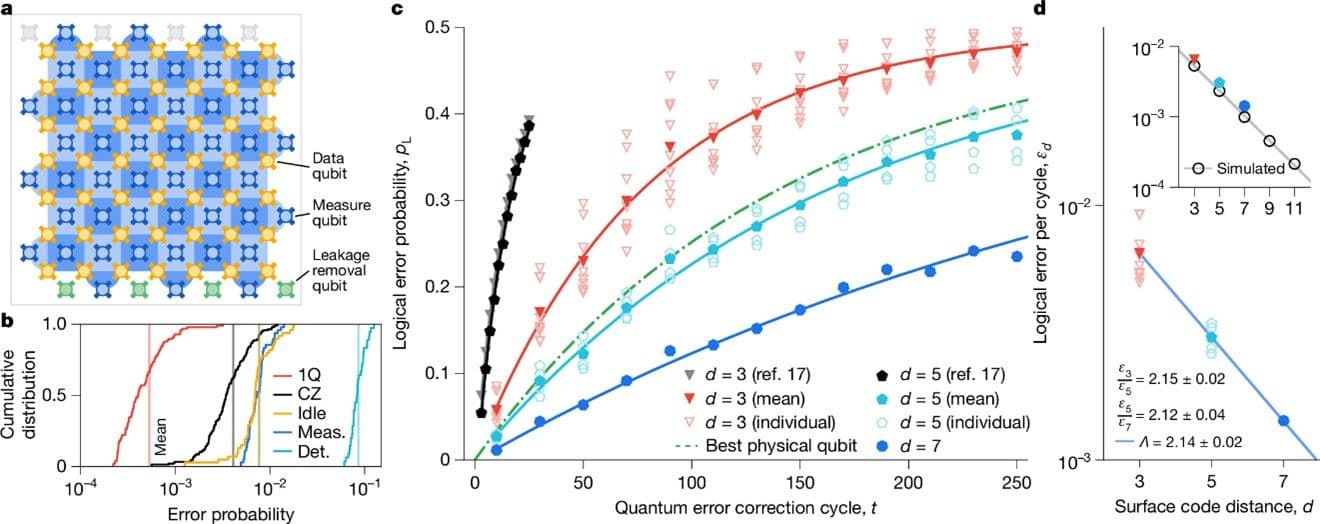
在眾多量子糾錯方案中，surface code因其只需近鄰耦合，且對局部錯誤具高度容忍性，被視為最適合超導量子電路實現的糾錯架構之一[18]。2024 年底，Google 宣布其超導量子處理器在實驗上首次明確展現 surface code 量子糾錯[19]。如圖三所示，隨著編碼距離 (code distance) $d$ 的增加，也就是使用更多實質量子位元來編碼單一邏輯量子位元，邏輯錯誤率持續下降，符合量子糾錯理論的預期，顯示量子糾錯確實進入有效運作的區域。此結果標誌著超導量子電腦發展中的一項關鍵里程碑。未來的核心挑戰，將是在有限且可工程化的實質量子位元數目下，持續提升量子位元品質與糾錯效率，使邏輯量子位元的錯誤率最終達到通用量子計算所需的 $10^{-12}$ 至 $10^{-16}$ 等級，真正邁向可規模化、具實用價值的量子電腦。

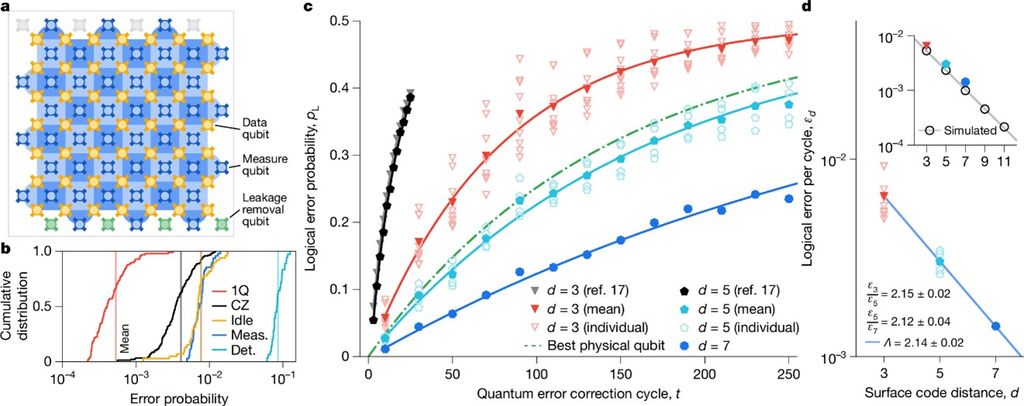
圖三：Google surface code 量子糾錯成果[19]。(a) 在 Willow 105 位元處理器上實作距離 $d = 7$ 的 surface code 示意圖。金色為形成 $d \times d$ 陣列的資料量子位元，藍色為量測量子位元，整體構成一個 $d = 7$ 的邏輯位元。(b) 量子位元處理器上控制量測的錯誤機率累積分布，包括單位元邏輯閘、雙位元 CZ 邏輯閘、資料量子位元閒置時的錯誤、狀態讀取識別錯誤。(c) 不同記憶時間下的邏輯錯誤機率。$d$ 越大，錯誤率越低，且使用 $d = 7$ 執行量子糾錯的邏輯位元錯誤率低於最佳實質位元的錯誤率，顯示量子糾錯具體成果。(d) 每循環邏輯錯誤率隨距離 $d$ 增加而降低。透過擬合決定誤差抑制參數 $\Lambda = 2.14$。（圖取自參考文獻[19]）

隨著量子糾錯實驗逐步取得突破，IBM 與 Google 等主要研究團隊相繼提出通往真正具備糾錯能力之量子計算（error-corrected quantum computing）的長期技術藍圖（roadmap），描繪超導量子電腦的發展路徑。以 Google 為例，其規劃可概略分為六個里程碑：首先，在特定任務上展現計算能力超越古典電腦；其次，利用約一百個實質量子位元，實驗性地證明量子糾錯能有效降低邏輯量子位元錯誤率；第三，將系統擴展至約一千個實質位元，使單一邏輯位元的錯誤率降至約10^-6；第四，實現對邏輯位元的可控制邏輯閘操作；第五，透過工程化方法擴充系統規模，建構包含約一百個邏輯位元的處理器；最終目標則是實現約一千個邏輯量子位元、且邏輯錯誤率可低至10^-13等級的通用型、具糾錯能力之量子電腦。至目前為止，前兩項里程碑已分別於2019年與2024年達成，而後續階段仍屬長期研究與工程挑戰，尚未設定明確完成時程。相較之下，IBM提出的roadmap在時間規劃上更為積極，目標是在2030年代初期，於超導量子電路平台上逐步完成模組化擴展與量子糾錯整合，並在約2033年具備實現數千個邏輯量子位元之通用型量子電腦的潛在能力。無論最終路徑與時程如何，這些roadmap皆清楚顯示，超導量子電腦的發展已由單純增加量子位元數目，正式邁入以量子糾錯、系統工程與可擴展性為核心的全新階段。

值得一提的是，去年諾貝爾物理獎得主，John Clarke在UC Berkeley、Michel Devoret在Yale、 與John Martinis在UC Santa Barbara，長期引領約瑟夫森接面與超導量子電路的實驗研究，奠定了今日超導量子位元的物理與工程基礎。當前投入超導量子電腦發展的主要公司，其技術與學術領導者很多與其有直接淵源。IBM超導量子電腦計畫的早期推手 Matthew Steffen 即出身於Martinis 的學術系統，而現今 IBM 量子部門的關鍵人物如Jay Gambetta、 Jerry Chow、Hanhee Paik等，也多承襲自此研究脈絡。2014年，Google更直接延攬Martinis及其 UCSB 團隊，成立 Quantum AI Lab，推動超導量子處理器的快速發展。新創公司方面，Rigetti創辦人Chad Rigetti為 Devoret 的學生，顯示學術傳承在產業化過程中的關鍵角色。近年來，Martinis創立Qolab，嘗試以半導體產業商用製程發展超導量子晶片；而 Devoret 於學術生涯後期亦加入 Google，持續投入量子工程研究。這些科學家不僅對超導量子電腦的誕生做出根本性貢獻，也持續以實際行動投入其中，反映出學界與產業界對超導量子電腦終將實現的深刻信念與期待。

在尚未達到真正具備糾錯能力的量子計算之前，且量子位元數目仍在數十至數千個的規模下，現階段的量子電腦通常被稱為Noisy Intermediate-Scale Quantum（NISQ）裝置，此一名詞由 John Preskill 於 2018 年提出[20]，用以描述當前量子硬體已有一定量子位元數量、但仍受雜訊與錯誤率限制的過渡階段。以Google的量子處理器Willow為例，可具體反映目前NISQ超導量子電腦的技術水準[19]。Willow 採用 105 個 transmon 量子位元，排列成二維網格拓撲，以支援 surface code 量子糾錯研究；其能量弛豫時間 $T_1$ 約為 70 至 100 $\mu$s，相干時間 $T_2$ 與之相當，單量子位元與雙量子位元閘的保真度分別約為 99.97% 與 99.9%，讀取保真度約 99.5%。雖然此類 NISQ 裝置尚不足以執行長深度、完全糾錯的量子演算法，但已在特定問題上展現應用潛力，例如利用變分量子演算法 (VQE)，在有限量子位元與電路深度下，模擬小型分子能譜或材料模型，是目前量子計算最具實驗可行性的應用之一。

另一方面，IBM亦在推動超導量子電腦生態系上扮演關鍵角色。自2016年 起，IBM率先透過 IBM Quantum Experience對外提供雲端存取的超導量子處理器，讓全球研究人員與學生能實際操作真實量子硬體。此一策略雖需投入大量硬體與維運資源，卻有效促進量子演算法、編譯技術與誤差抑制方法的快速發展。透過開放雲端平台，IBM不僅能蒐集使用者在實際量子計算任務中的需求與創意，也能從大量使用回饋中辨識硬體瓶頸與系統性誤差，反過來優化量子位元設計、控制方法與整體架構。這種硬體與使用者共同演化的發展模式，對於加速超導量子電腦由實驗室研究走向可擴展工程系統，發揮了深遠影響。

美國以外，世界其他科技大國，包含歐洲、日本等，也加大力道發展超導量子電腦，特別是中國長期且系統性地投入，相關研究多以國家級科研計畫與大型研究機構為主導，並與大學密切合作。近年來，中國研究團隊也在特定任務上展示量子計算能力超越古典電腦的實驗成果[21,22]。整體而言，其發展節奏與國際主要研究團隊高度同步，往往能在國際重要里程碑發表後的一至數年內，完成具可比性的實驗示範。這顯示超導量子電腦已成為全球高度競逐的前沿科技，將其視為未來資訊科技與基礎科學的重要戰略方向。

超導量子電腦的挑戰

要真正實現具備量子糾錯能力的通用型量子計算，仍需克服多項根本挑戰，其中系統擴充與量子位元錯誤率同等重要。John Martinis曾明確指出，通往糾錯量子計算的路徑並非僅靠增加量子位元數目，必須同時持續降低單位元、雙位元邏輯閘與讀取的錯誤率。圖四所示的概念性圖表，是Google用以說明量子處理器在量子位元數目與操作錯誤率之間所需同時推進的發展方向，此一觀點亦與quantum volume等量子處理器綜合性效能指標的精神相呼應。量子位元的錯誤來源與其相干時間、材料與製程缺陷、以及控制與讀取精度密切相關。特別值得注意的是，超導量子位元本質上屬於連續變數的類比系統，其操控仰賴精細調制的類比微波脈衝，然而量子邏輯閘卻要求高度可重現的數位化操作結果。這種以類比控制實現數位邏輯的根本張力，使得控制電子學、脈衝成形技術與校準方法，成為降低錯誤率、推進超導量子電腦發展的關鍵工程課題之一。

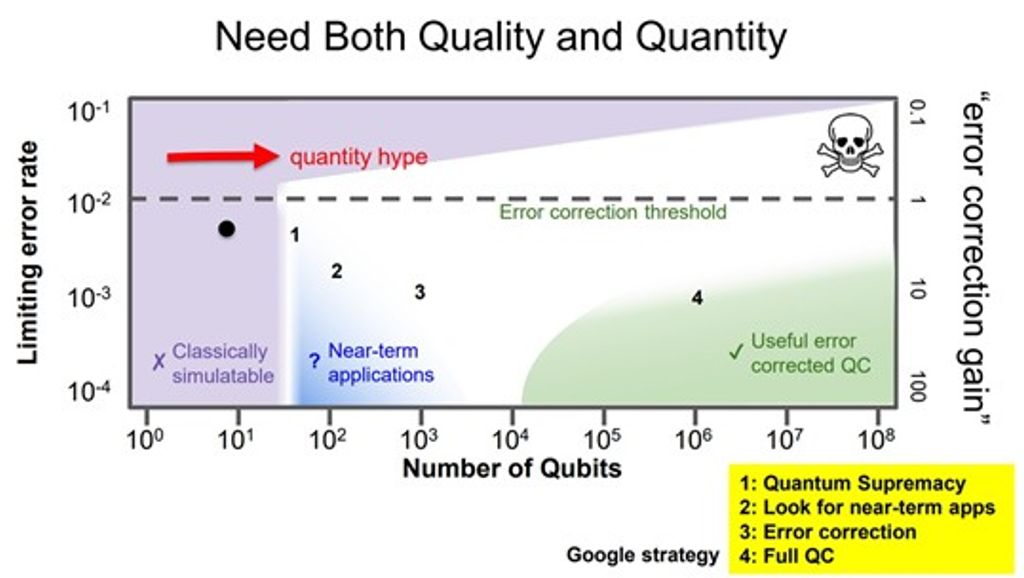圖四：超導量子電腦在位元數目與錯誤率間發展進程選擇的二維概念圖。Google Quantum AI的研究發展方向以數字標記，目標是實現具備糾錯能力的量子電腦，並在過程中探索近程應用。
（圖取自HPCwire網站 https://www.hpcwire.com/2018/04/26/google-frames-quantum-race-as-two-dimensional/）

量子位元的相干時間 $T_2$ 與其能量弛豫時間 $T_1$ 密切相關，也是影響量子閘錯誤率的關鍵指標。過去二十五年間，超導量子位元的 $T_1$ 已取得驚人進展，從最早期僅數奈秒的紀錄，提升約 $10^5$ 倍，目前 transmon 量子位元的 $T_1$ 已突破 1 毫秒等級[23]。圖五整理了超導量子位元 $T_1$、$T_2$ 的歷史演進[24]。以典型邏輯閘操作時間約 50 奈秒估計，若期待單個邏輯閘錯誤率達到 $10^{-4}$，量子位元的相干時間至少需在 500 微秒以上。錯誤率越低，則能以更少的實質量子位元實現邏輯位元，對系統擴充性更有利。因此，延長量子位元的相干時間仍然是超導量子電腦工程的重要課題，也是降低錯誤率、達成糾錯量子計算的基礎條件之一。

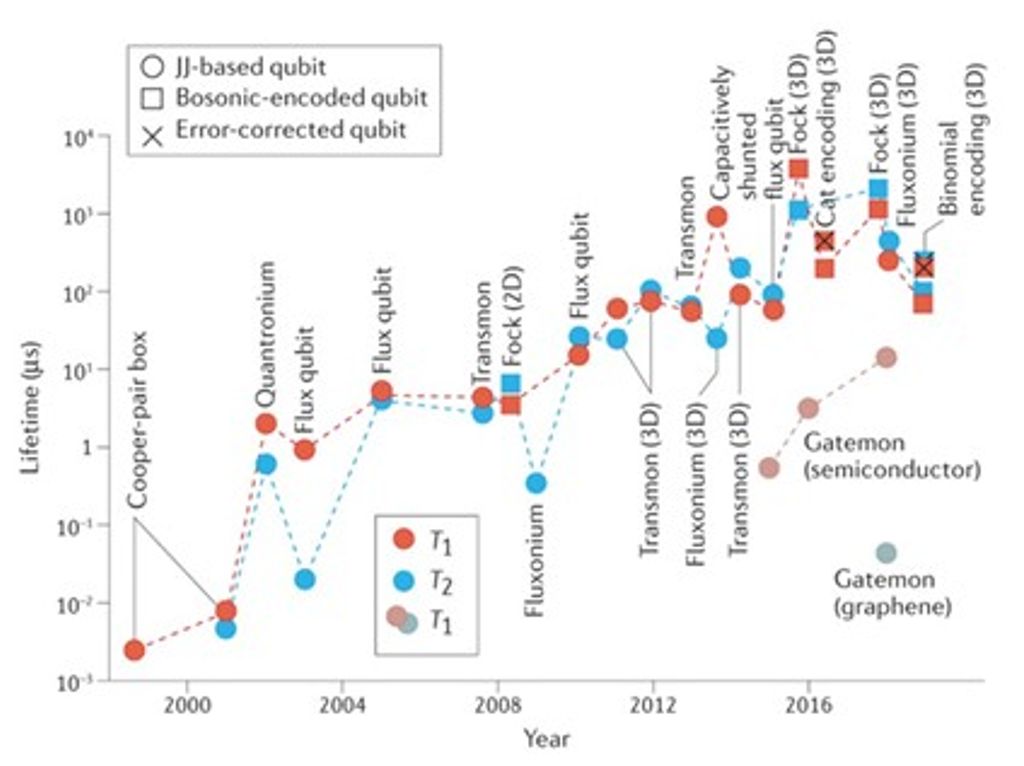圖五：超導量子位元的相干時間 ($T_1$、$T_2$) 從 1999 年以來的演進資料[24]，並涵蓋以微波腔光子編碼的架構以及採用錯誤緩解技術的裝置。（圖取自參考文獻[24]）

目前已知影響超導量子位元T_1的主要機制可概分為數類。首先，量子位元的控制與讀取線路會不可避免地將量子位元耦合至外在環境，導入額外的輻射與阻抗損耗。此類損耗可透過電路設計加以抑制，例如最佳化耦合電容或互感大小、加入濾波器與阻抗轉換結構，以在操控效率與環境隔離之間取得平衡。其次，量子位元材料與其介面缺陷亦是能量耗散的重要來源。特別是在金屬/介電層或金屬/基板介面中，往往存在高密度的兩能階系統（two-level systems, TLS），會與量子位元電場耦合並吸收能量。降低此類損耗的策略包括改善薄膜與基板製程品質、選用低損耗材料，以及透過電路幾何設計，減少電磁能量分佈於高缺陷密度介面中的比例[25,26]。

另一項關鍵機制為超導體內準粒子（quasiparticle）濃度過高所導致的能量耗散。準粒子的產生可能來自多種因素，包括有偏高的環境溫度、黑體輻射中遠紅外光對晶片的照射[27]、宇宙射線及其產生的次級粒子撞擊晶片[28]、以及薄膜或封裝材料中的機械應力釋放所引發的聲子激發[29]。這些作用皆可能破壞古柏對，增加準粒子濃度，進而與量子位元耦合造成能量損失。對應的抑制方法包括提升晶片與冷頭之間的熱連結以確保有效降溫、加強光學遮蔽以阻絕遠紅外光輻射、利用高原子序材料或地下設施降低宇宙射線通量[30]、或藉由聲子阻斷結構減少能量在晶片內的傳播[31]、搭配適當的真空膠選擇與烘烤程序以釋放封裝應力。

此外，在量子位元狀態讀取過程中，為了提高讀取保真度或縮短讀取時間，往往需要施加較強的微波讀取訊號；然而，過高的讀取功率可能引發量子位元的躍遷[32]，進而縮短其有效相干時間。因此，讀取設計必須在讀取精度與對量子位元狀態干擾之間取得最佳折衷，這亦是目前超導量子電腦系統工程中持續優化的重要課題。

除了單一量子位元本身的性能外，系統規模擴充（scalability）是超導量子電腦邁向糾錯計算時所面臨的另一項核心挑戰。在現行架構中，從室溫電子設備延伸至低溫量子晶片的控制與讀取線路，隨量子位元數目等比例增加，同時引入相應的熱負載。然而，極低溫設備稀釋製冷機在mK溫度區域所能提供的冷卻功率極為有限，實際上僅能支撐約數千至上萬條低溫線路。這一限制對於未來需容納百萬個實質量子位元的糾錯量子電腦而言，構成明顯且迫切的系統瓶頸。

為緩解此問題，低溫CMOS控制電路（cryoCMOS）已成為重要的發展方向之一，其核心理念是在約 4 K 環境中實現穩定運作的控制與讀取電路，並將部分控制功能由室溫下移至低溫級板，從而大幅減少自室溫延伸至低溫的控制線路數目與對冷卻系統的負擔。更具前瞻性的構想則是採用由約瑟夫森接面構成的單一磁通量子（Single Flux Quantum, SFQ）邏輯電路[33]，可於 mK 環境下運作，並以極低能耗產生精確的數位脈衝；若能與量子位元有效整合，將有潛力大幅降低室溫至 mK 的控制線路需求。另一種替代途徑是利用光纖引入光學訊號，並在低溫端透過轉頻器將其轉換為微波訊號以操控量子位元[34]，由於光纖的熱導極低，此方法在熱負載管理上具有潛在優勢。

此外，隨著系統規模擴大與控制精度要求提高，控制線路間的串擾（crosstalk）亦成為不可忽視的工程挑戰。在小規模量子處理器中，串擾已會影響控制脈衝的準確性；在大規模且高保真度需求的量子處理器中，其影響更為顯著。因此，未來的超導量子電腦系統必須結合周密的電磁屏蔽與接地設計、合理的線路佈局，以及高度一致性的製程工藝，方能有效抑制串擾，確保量子控制在大規模系統中的可靠運作。

目前主流的超導量子電腦架構中，所使用的量子位元多以電路系統的最低能階本徵態作為計算基底。在此架構下，實現量子糾錯最成熟的方法為 surface code，其需透過大量實質量子位元來編碼單一邏輯量子位元。前述 Google 已成功示範利用 surface code 實現邏輯錯誤率隨編碼距離增加而下降，顯示量子糾錯在超導電路中的可行性，然而其對量子位元數目、控制複雜度與系統穩定性的要求極高，工程難度不容小覷。

另一方面，Daniel Gottesman、Alexei Kitaev、與John Preskill（GKP）於2001年提出以連續變數系統編碼量子資訊的構想，利用共振器中具有週期性相空間結構的GKP狀態來表示一個邏輯量子位元[35]，其最大優勢在於單一物理共振器即可承載具糾錯能力的邏輯量子位元，能有效修正小幅位移型錯誤。近年來，超導電路平台已在此方向取得重要進展，實驗上成功製備近似GKP狀態，並示範透過持續量測讀取與回饋機制降低邏輯錯誤率[36]。GKP 量子位元為實現糾錯量子計算提供了不同於 surface code 的路徑，具有潛在的資源效率優勢。然而，其在邏輯閘操作上的挑戰依然顯著，一旦需要在多個 GKP 量子位元之間引入耦合以實現邏輯閘，系統的控制複雜度、誤差傳播與狀態保真度維持，都成為高度非平凡的問題。因此，如何在保持糾錯優勢的同時，實現高保真度的多量子位元邏輯操作，仍是 GKP 架構邁向實用量子計算所需突破的關鍵課題之一。

結語

回顧超導量子電腦的發展歷程，可以看見一條由競爭、合作到共同開放所交織而成的道路。早期學界之間高度交流，研究成果迅速共享，使超導量子電路在材料、控制與系統工程上得以快速累積進展。然而，隨著量子電腦逐步走向商業化，國際競爭加劇，資訊交流趨於保守，如何在保護智慧財產與維持學術開放之間取得平衡，將成為影響整體技術進展速度的重要課題。

從全球角度來看，各國與研究機構已大舉投入量子科技發展。歐洲 IMEC 已啟動 12 吋超導量子積體電路相關研究[37]，顯示量子電腦正逐步邁向與先進半導體製程深度整合的階段。在此背景下，台灣長期累積的半導體製造與製程整合經驗，使其在超導量子積體電路的發展上備受國際期待。中研院於南部院區關鍵議題研究中心建置量子電腦專題中心，其中 QC-Fab 專注於 8 吋超導量子積體電路製程開發，QC-Test 則致力於量子晶片效能的量測與系統展示。近期中研院團隊更與 Qolab 合作，成功以 8 吋半導體相容製程製作 window junction 量子位元，並展示 $T_1$ 可達 57 $\mu$s[38]，具體驗證了以成熟製程推動超導量子電路的可行性。

展望未來，超導量子電腦的發展或許不應僅侷限於單一平台，而需與量子網路、光學系統等其他量子技術相互連結，加速邁向具實用價值的量子計算能力。最終，量子電腦的目標不僅是技術突破本身，更在於促進科學研究、產業創新與整體社會福祉。如何在競爭中保持合作精神，並善用各地的技術優勢，將是下一階段量子科技能否真正落地的關鍵。

 

參考文獻：
[1]    J. C. Bardeen, L. N.J. R. Schrieffer, J. R., Physical Review 108, 1175 (1957).
[2]    B. D. Josephson, Physics Letters 1, 251 (1962).
[3]    P. W. Anderson and J. M. Rowell, Physical Review Letters 10, 230 (1963).
[4]    A. J. Leggett, Progress of Theoretical Physics Supplement 69, 80 (1980).
[5]    M. H. Devoret, J. M. Martinis, and J. Clarke, Physical Review Letters 55, 1908 (1985).
[6]    J. M. Martinis, M. H. Devoret, and J. Clarke, Physical Review Letters 55, 1543 (1985).
[7]    R. P. Feynman, International Journal of Theoretical Physics 21, 467 (1982).
[8]    P. W. Shor, Siam Journal on Computing 26, 1484 (1997).
[9]    Y. Nakamura, Y. A. Pashkin, and J. S. Tsai, Nature 398, 786 (1999).
[10]    J. Clarke and F. K. Wilhelm, Nature 453, 1031 (2008).
[11]    A. Blais, R. S. Huang, A. Wallraff, S. M. Girvin, and R. J. Schoelkopf, Physical Review A 69, 062320 (2004).
[12]    A. Wallraff, D. I. Schuster, A. Blais, L. Frunzio, R. S. Huang, J. Majer, S. Kumar, S. M. Girvin, and R. J. Schoelkopf, Nature 431, 162 (2004).
[13]    J. Koch et al., Physical Review A 76, 042319 (2007).
[14]    A. Place et al., Nature Communications 12, 1779 (2021).
[15]    R. Barends et al., Physical Review Letters 111, 080502 (2013).
[16]    Y. Pashkin, T. Yamamoto, O. Astafiev, Y. Nakamura, D. Averin, and J. Tsai, Nature 421, 823 (2003).
[17]    F. Arute et al., Nature 574, 505 (2019).
[18]    A. G. Fowler, M. Mariantoni, J. M. Martinis, and A. N. Cleland, Physical Review A 86, 032324 (2012).
[19]    R. Acharya et al., Nature 638, 920 (2025).
[20]    J. Preskill, Quantum 2, 79 (2018).
[21]    Y. L. Wu et al., Physical Review Letters 127, 180501 (2021).
[22]    D. Gao et al., Physical Review Letters 134, 090601 (2025).
[23]    M. P. Bland et al., Nature 647, 343 (2025).
[24]    I. Siddiqi, Nature Reviews Materials 6, 875 (2021).
[25]    J. Wenner et al., Applied Physics Letters 99 (2011).
[26]    C. Wang, C. Axline, Y. Y. Gao, T. Brecht, Y. Chu, L. Frunzio, M. H. Devoret, and R. J. Schoelkopf, Applied Physics Letters 107 (2015).
[27]    T. Connolly, P. D. Kurilovich, S. Diamond, H. Nho, C. G. L. Bøttcher, L. I. Glazman, V. Fatemi, and M. H. Devoret, Physical Review Letters 132, 217001 (2024).
[28]    C. D. Wilen et al., Nature 594, 369 (2021).
[29]    R. Anthony-Petersen et al., Nature Communications 15, 6444 (2024).
[30]    G. Bratrud et al., Nature Communications 16, 9906 (2025).
[31]    V. Iaia, J. Ku, A. Ballard, C. P. Larson, E. Yelton, C. H. Liu, S. Patel, R. McDermott, and B. L. T. Plourde, Nature Communications 13, 6425 (2022).
[32]    D. Sank et al., Physical Review Letters 117, 190503 (2016).
[33]    C. H. Liu et al., PRX Quantum 4, 030310 (2023).
[34]    G. Arnold, T. Werner, R. Sahu, L. N. Kapoor, L. Qiu, and J. M. Fink, Nature Physics 21, 393 (2025).
[35]    D. Gottesman, A. Kitaev, and J. Preskill, Physical Review A 64, 012310 (2001).
[36]    V. V. Sivak et al., Nature 616, 50 (2023).
[37]    J. Van Damme et al., Nature 634, 74 (2024).
[38]    C.-T. Ke et al., arXiv e-prints, 2503.11010 (2025).
[39]    J. Clarke, A. N. Cleland, M. H. Devoret, D. Esteve, and J. M. Martinis, Science 239, 992 (1988).