微中子振盪:通往新物理的大門
在前刊《無所不在的幽靈粒子——微中子探秘》中,我們介紹了微中子的發現史、基本物理性質,以及它們在宇宙學中的角色。然而,隨著實驗技術的進展,物理學家逐漸意識到,微中子不僅僅是「難以捉摸」的粒子,它們的行為本身,甚至正在挑戰我們對基本粒子與自然界對稱性的既有認知。
本文將聚焦於一個看似反直覺、卻極具深遠意義的現象——微中子振盪。正是這項發現,首次明確指出微中子並非如標準模型所假設的那般簡單,也開啟了通往輕子混合、質量生成,以及潛在的 CP 破壞等關鍵議題的大門。
一、探測簡史:消失的微中子何去何從?
微中子是宇宙中數量最多的費米子,也是僅次於光子、最無所不在的基本粒子。我們先來複習一下微中子家族。它們的種類分別是:電子(e)微中子、緲子(μ)微中子、淘子(τ)微中子——在物理學上,我們稱之為三種「味」(flavor)。它們質量幾乎為零(注意這邊用的詞是「幾乎」)、也因此幾乎都趨近光速運動;此外,微中子只參與重力、弱交互作用,因此並不像光子那樣能輕易被感測到。綜合這兩大特性,這便可以解釋了為什麼每秒有數兆個微中子穿過你我的身體、我們卻從未感知到——對於微中子而言,所有物質、就算是最精密的探測器擺在面前,幾乎都是透明的——而光是這點,就足以讓這個看似無所不在的粒子、成為最「難以捉摸」的幽靈粒子。
那麼,微中子是從哪來的?
對於地球而言,太陽是微中子的最大產生源。86%的太陽微中子(solar neutrinos)會從核融合的質子-質子鏈反應中產生,由於參與反應的是電子,因此太陽微中子基本上就是電微中子。而在1960年代晚期的霍姆斯特克實驗(Homestakes experiment)中,人們發現:實驗探測到的微中子數量,僅有預測數量的約1/3——這就是著名的「太陽微中子問題」(solar neutrino problem)。於是物理學家們做出了這樣的猜想:會不會是這些電子微中子在抵達地球被觀測前,轉變成其他型態(味)的微中子,導致了數量上的缺陷?而這個假說就是「微中子振盪」(neutrino oscillation)理論的雛形。直到將近三十幾年後的2001年,加拿大薩德伯里微中子觀測站(Sudbury Neutrino Observatory, SNO)的實驗,驗證了微中子會發生「味變換」的說法,可以視為微中子振盪的首個實驗論證。
而微中子的產生源並不止於太陽,當宇宙射線與大氣層交互作用時,也會產生微中子。這類大氣微中子(atmosphric neutrinos)最常見的莫過於緲微中子,畢竟緲子(muon)算是最容易被地表觀測到的宇宙射線之一(圖1-1)。日本超級神岡探測器(Super-Kamiokande)在1998年發現了類似太陽微中子的「數量缺失」,而後也被證實了就是大氣微中子的振盪現象。
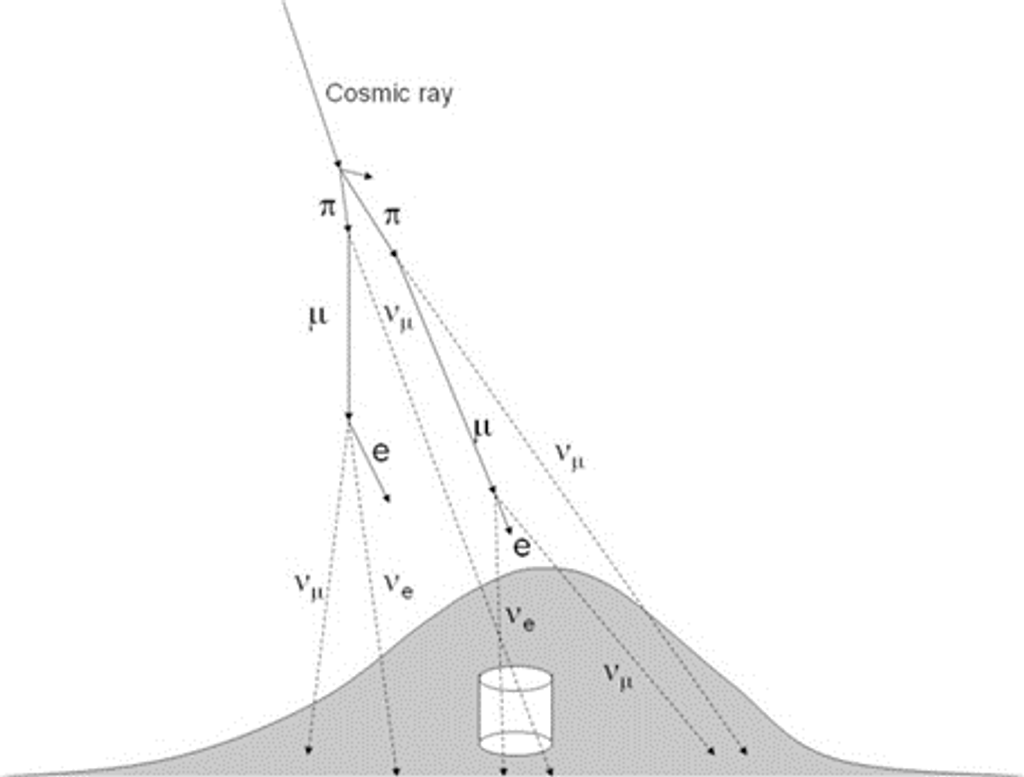 圖 1-1:以緲子 ($\mu$) 為主的宇宙射線,是大氣微中子的主要探測來源。圖源:Takaaki Kajita in the Proceedings of the Japan Academy, Series B, Physical and Biological Sciences (10.2183/pjab.86.303)
圖 1-1:以緲子 ($\mu$) 為主的宇宙射線,是大氣微中子的主要探測來源。圖源:Takaaki Kajita in the Proceedings of the Japan Academy, Series B, Physical and Biological Sciences (10.2183/pjab.86.303)
領導SNO實驗的亞瑟·麥克唐納(Arthur McDonald)和超級神岡探測器的梶田隆章,也因此獲頒2015年的諾貝爾物理學獎(圖1-2),根據官方說法,其成就在於:
「觀測到微中子振盪,並因此證明了微中子具有質量」
(“For the discovery of neutrino oscillations, which shows that neutrinos have mass”)
讀到這裡,大家應該就知道微中子振盪的實驗沿革了。然而這裡我們卻忽略了一個核心問題:微中子振盪何以成為微中子具有質量的鐵證?
 圖1-2: 2015年諾貝爾物理學獎的官方海報,獲獎者分別是梶田隆章(左)與亞瑟·麥克唐納(右)。圖源:http://www.nobelprize.org/nobel_prizes/physics/laureates/2015/
圖1-2: 2015年諾貝爾物理學獎的官方海報,獲獎者分別是梶田隆章(左)與亞瑟·麥克唐納(右)。圖源:http://www.nobelprize.org/nobel_prizes/physics/laureates/2015/
二、微中子振盪:顛覆標準模型的粒子行為?
我們在之前的文章中已經展示過微中子振盪的數學模型、也推導出了微中子振盪的機率形式,這裡帶大家簡單複習一下。
儘管關於微中子質量究竟如何生成,目前仍缺乏一個確立的理論機制,但微中子振盪本身其實相對容易理解——甚至只需要大學程度的量子力學概念便足以說明。一句話總結就是:微中子振盪源於「質量特徵態」與「味特徵態」並不重合這個事實。
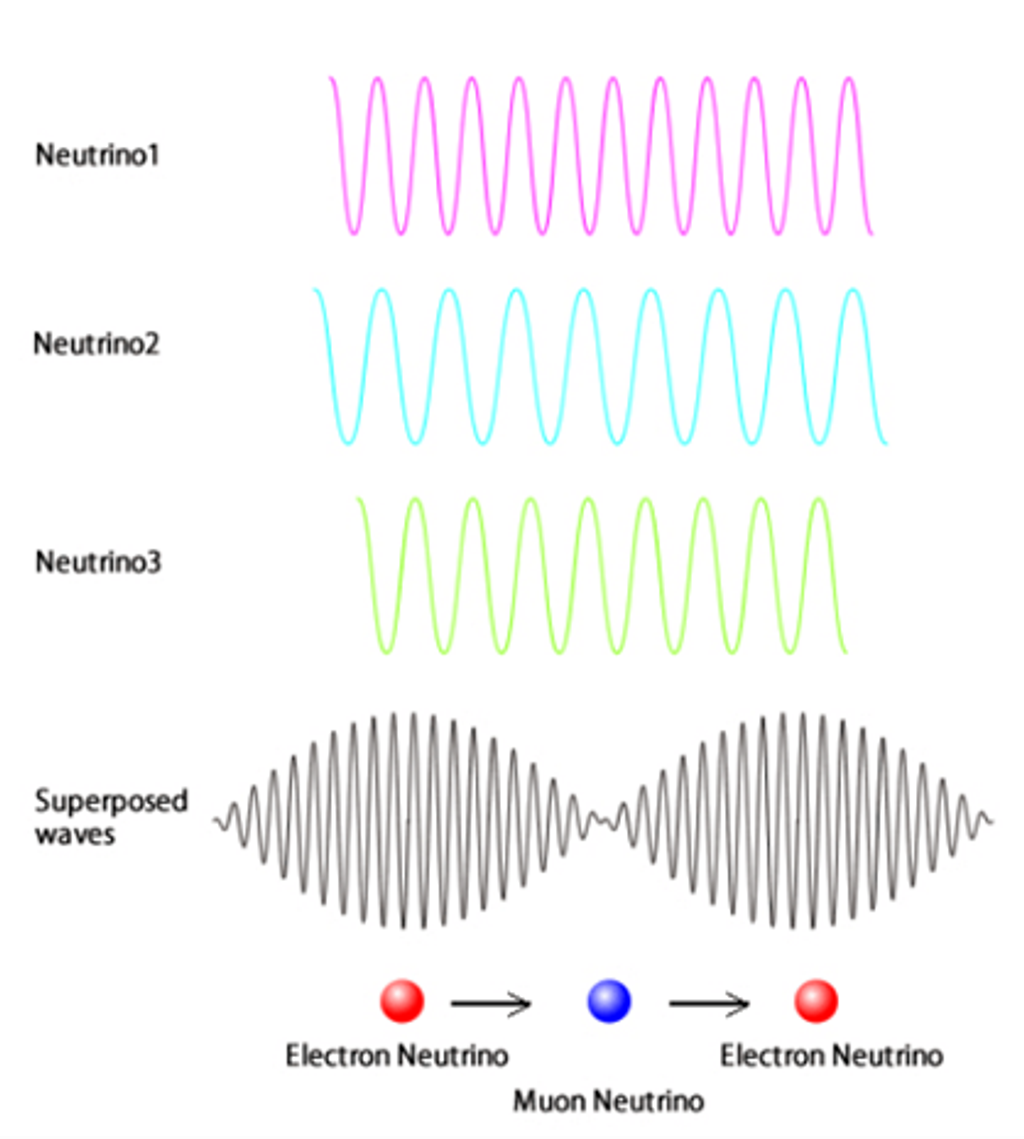 圖2-1: 以「波段」的疊加來理解微中子振盪:不同味的微中子可以視為不同頻率的波段,任兩者的疊加則可形成「波包」,當振盪發生時,相當於轉變成不同的味特徵態,圖中是以緲微中子與電微中子為例。圖源:https://www-sk.icrr.u-tokyo.ac.jp/en/sk/neutrino/kajita/vibration/
圖2-1: 以「波段」的疊加來理解微中子振盪:不同味的微中子可以視為不同頻率的波段,任兩者的疊加則可形成「波包」,當振盪發生時,相當於轉變成不同的味特徵態,圖中是以緲微中子與電微中子為例。圖源:https://www-sk.icrr.u-tokyo.ac.jp/en/sk/neutrino/kajita/vibration/
現今粒子物理學建立在量子場論的框架之上,而場論的數學基礎來自量子力學。量子力學本質上則是一套建構於向量空間之中的理論,它告訴我們,粒子可以處於各種不同的「狀態」、用線性代數的語言就是特徵態(eigenstate),而不同的物理過程,往往偏好用不同的基底(basis)來描述。哪些狀態會被「觀測」,取決於我們探測的行為——還記得嗎?量子力學本身強調的,無非就是觀測的行為與狀態之間的交互作用。對微中子而言也是如此:在自由空間中傳播時,最自然的描述方式是質量特徵態;而一旦參與弱交互作用、從而被探測器「感測」,我們所量測到的將會是味特徵態。就像是我們在見到一個人時,通常可以立刻描述對方的外表、衣著(味特徵態),但我們卻無法直接說出對方的體重數值(質量特徵態)。
微中子振盪之所以發生的關鍵在於:「質量」和「味」這兩組特徵態並不相同。我們在實驗中所稱的「電微中子」、「緲微中子」或「淘微中子」,其實都不是單一的量子態,而是多個質量特徵態的疊加。就像之前提過的,如果用紅、綠、藍三原色來類比微中子的質量或味特徵態,那麼所謂的「電子微中子」,或許更像是黃色——也就是紅色與綠色以特定比例混合後的結果;而這些混合的比例,正是由所謂的「混合角」(mixing angle)所決定。混合的比例決定了振盪的程度;若混合角為零,則振盪就不會發生。正因為質量特徵態彼此具有不同的質量,它們在傳播過程中會累積不同的量子相位,這種相位差隨著時間與距離改變,最終使得微中子被觀測到的「味」發生轉換——這便是我們所說的微中子振盪。
微中子振盪的行為可以用下列式子表述:
$$|\nu_i\rangle = \sum_j U_{ij} |\nu_j\rangle,$$ (1)
從上面不難看出,味特徵態 ($i \in e, \mu, \tau$) 可以視為質量特徵態 ($j \in 1, 2, 3$) 的疊加,且味變換可以透過么正矩陣 $U_{ij}$ 來聯繫。我們在之前的文章中用了簡化版的雙味近似 (two-flavor approximation) 來推導,所得到的振盪機率方程會是:
$$P(\nu_\alpha \rightarrow \nu_\beta) = |\langle \nu_\beta | \nu_\alpha(t) \rangle|^2 = \sin^2 2\theta \sin^2 \left( \frac{\Delta m^2 L}{4E} \right)$$(2)
這裡 $\theta$ 代表混合角,$m$、$L$ 與 $E$ 分別代表微中子的質量、傳播距離以及能量。那麼,微中子振盪又如何佐證了微中子「質量非零」的事實?我們不妨換個角度思考:如果微中子質量為零,三種微中子將自然而然滿足 $m_1 = m_2 = m_3 = 0$,而這也正是標準模型原先的假設。然而,實驗率先觀測到了微中子振盪——而振盪的存在,意味著不同質量特徵態發生相位疊加,這只有在質量平方差 ($\Delta m^2$) 非零的情況下才可能發生(留意式(2)的質量項)。換言之,至少必須存在某些不相等的質量特徵態,例如 $m_1 \neq m_2$(不論第三個質量為何),這便直接導致一個不可避免的結論:至少有一種微中子質量不為零。僅憑這一點,就已足以打破標準模型既有的框架。至於標準模型為何會有「微中子質量為零」的設定,我們已在前文討論過,這裡不再贅述。
三、PMNS矩陣:隱藏其中的宇宙學謎團
現在讓我們回到式(1),這條式子表達了微中子振盪的行為。值得注意的是,在推導式(2)時我們採用了簡化版、即只考量兩種味特徵態的微中子,因此 $U_{ij}$ 是個簡單的二階矩陣。但廣義來說,如果我們考量三種微中子的特徵態,這個矩陣將可以寫成如下形式:
$$U_{\text{PMNS}} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & c_{23} & s_{23} \\ 0 & -s_{23} & c_{23} \end{pmatrix} \begin{pmatrix} c_{13} & 0 & s_{13}e^{-i\delta_{CP}} \\ 0 & 1 & 0 \\ -s_{13}e^{i\delta_{CP}} & 0 & c_{13} \end{pmatrix} \begin{pmatrix} c_{12} & s_{12} & 0 \\ -s_{12} & c_{12} & 0 \\ 0 & 0 & 1 \end{pmatrix}$$(3)
這看似比想像中複雜不少的矩陣形式,就是代表輕子家族的「PMNS矩陣」(Pontecorvo-Maki-Nakagawa-Sakata matrix)。在粒子物理學中,三代夸克的弱交互作用是由CKM矩陣(Cabibbo-Kobayashi-Maskawa matrix)所描述的,同樣也是一個3x3矩陣。
這兩種矩陣的共通點在於:它們皆包含了三個混合角、以及一個 CP 相位因子。在式(3) 中,$s = \sin \theta$,$c = \cos \theta$,代表了混合角;$\delta$ 則是相位因子,在這裡表示 CP 破壞的相位,若 $\delta_{CP}$ 非零,則說明了微中子振盪具有 CP 破壞的性質——這將成為提供理解宇宙早期物質與反物質不對稱的重要線索,也是當前與未來中微子實驗所高度關注的核心問題之一。從實驗物理學的角度來論,我們所能量測到的關鍵參數,無非就是三個混合角 ($\theta_{12}$, $\theta_{23}$, $\theta_{13}$) 以及 CP 相位 ($\delta_{CP}$)。一旦這些參數被更精確地量測出來,它們不僅能完整描述微中子振盪的行為,也將成為連結理論模型與實驗觀測的關鍵橋樑——而這,正是現代微中子實驗的重點目標。
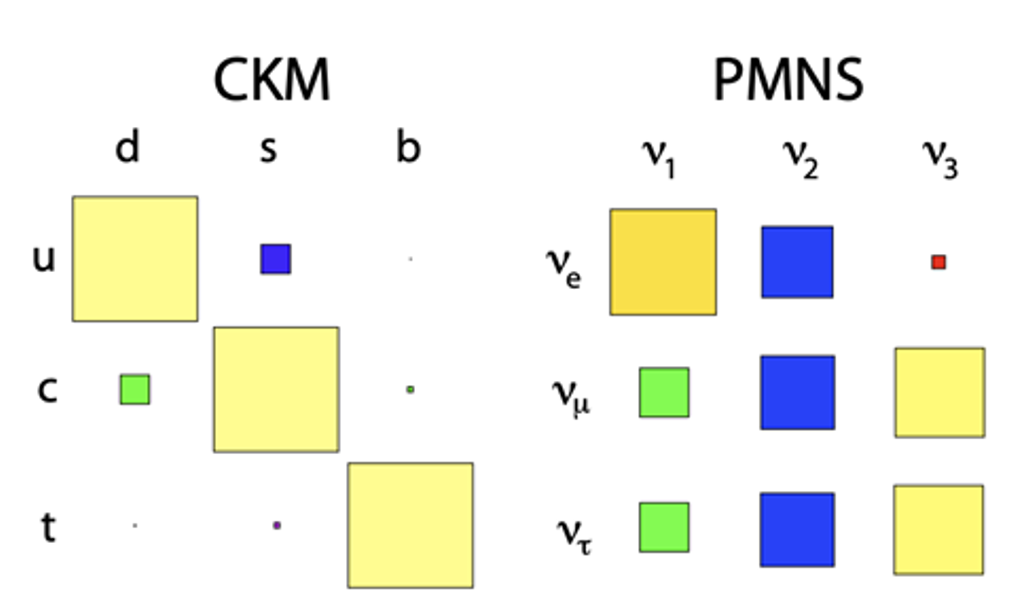
圖 3-1:描述夸克混合的 CKM 矩陣(左)與描述微中子混合的 PMNS 矩陣(右)。方塊的面積大小代表該矩陣元素的平方 $|U_{ij}|^2$,也就是該味特徵態包含某一質量態的比例。CKM 矩陣幾乎由對角線上的元素主導,意味著夸克的味與質量特徵態高度一致、混合效應相對微弱;PMNS 矩陣中的多個元素都具有相近且顯著的大小,顯示微中子具有較大的混合幅度。此一差異也意味著輕子與夸克的質量生成、混合,可能源自不同的物理機制。圖源:Sheldon Stone, DOI: 10.22323/1.174.0033
相較於夸克家族的CKM矩陣,人們對於輕子家族的PMNS矩陣尚未理解透徹。CKM矩陣的參數在過去數十年間已被精確驗證,比如CP相位因子不為零、這就足以解釋了K介子衰變中的CP破壞。然而對於PMNS矩陣中的CP相位究竟是否為零,至今依然有待驗證,這也是當前實驗探測的首要任務。從這點也不難看出,微中子的探測難度比夸克來得高。
四、持續解碼:21世紀的實驗展望
回到 PMNS 矩陣,如果你仔細端詳式(3),便會發現,$\theta_{12}, \theta_{23}, \theta_{13}$ 分別嵌於三塊矩陣中,其中只有中間那方陣包含有 CP 相位因子。事實上,這三個被拆分的矩陣各自代表著不同類型的實驗意義:
| PMNS矩陣項 | 振盪模式 | 粒子源 | 實驗代表 |
| $\theta_{23}$ 矩陣(左) | 𝜈μ →𝜈τ | 大氣微中子/加速器 | Super-Kamiokande, IceCube, T2K, NOvA |
| $\theta_{13}$ 矩陣(中) | 𝜈e → 𝜈e 𝜈μ → 𝜈e | 加速器/核反應爐 | T2K, NOvA, DUNE, Daya Bay, RENO, Double Chooz |
| $\theta_{12}$ 矩陣(右) | 𝜈e → 𝜈μ/𝜈τ | 太陽微中子/反應爐 | SNO, Super-Kamiokande, Borexino, KamLAND |
而我們在前一章節已經討論過太陽微中子與大氣微中子的實驗了——這兩項的觀測足以支持微中子振盪的存在,但卻還不足以量測CP相位。因此,第三種實驗類型就派上用場了——加速器實驗。這類型的微中子並非直接來源於自然界,而是透過核反應爐、或者粒子加速器的撞擊與衰變所產生。
對於這類型的微中子實驗,最常用到的方程式莫過於以下這條:
$$P(\nu_\alpha \to \nu_\beta) = \sin^2 2\theta \sin^2 \left( 1.27 \frac{\Delta m^2 [\text{eV}^2] L [\text{km}]}{E [\text{GeV}]} \right)$$ (4)
這條公式其實就是式(2)的SI制版本,它表述了任兩種微中子發生味特徵態轉變 $\alpha \to \beta$ 的機率。從方程式可以看出,微中子振盪的機率除了取決於混合角 $\theta$ 以外,也取決於能量 $E$ 與距離 $L$。這也間接催生出了加速器實驗的優勢:我們可以掌握粒子源的能量,同時設定微中子傳播的基線 (baseline) 長度。
如果CP破壞存在,就意味著以下不等式將會成立:
$P(\nu_\alpha \to \nu_\beta) \neq P(\bar{\nu}_\alpha \to \bar{\nu}_\beta)$
因此這時探測的重點就在於「反微中子」的數量了,我們可以從探測到的正、反微中子比值,來推斷出CP破壞是否存在。對於太陽或者大氣微中子實驗而言,不是反微中子的數量相當有限、就是比例和能量分布特別複雜。因此,諸如加速器這類的「人造」微中子實驗反而會更直觀,因為我們將能更精確地掌控粒子的生成、衰變與分支比(branching ratio)等等,才更有機會將微妙的不對稱性從實驗數據中體現出來,而這類型的實驗也成為當代微中子探測器的開發重點。
五、結語
至此,數十年下來的實驗已經向我們闡明:微中子振盪並非只是某種數學上的巧合,而是深深植根於量子力學與粒子物理結構中的現象。從特徵態的可區辨性到PMNS 矩陣的推廣,這些看似抽象的參數,實際上承載著關於微中子質量、CP破壞,甚至宇宙早期演化的重要線索。
那麼,物理學家究竟是如何追蹤這些幾乎不與物質互動的粒子?實驗又必須如何被精心設計,才能在雜訊之中捕獲微弱而關鍵的訊息?在下一篇文章中,我們將把目光從理論轉向實驗,介紹微中子的主要探測方式、加速器微中子實驗的基本原理。現今對於微中子物理圖像的建立,是從極其稀少的交互作用事件中,一次又一次地重建、推論與驗證而來。微中子物理因此成為一門橫跨理論與實驗邊界的學問——它既挑戰我們對自然界基本架構的理解,也迫使實驗物理不斷突破探測技術的極限。

