
計算新時代的最早應用之一,也許是模擬驅動化學反應的量子效應。
想到化學,「量子」(quantum)也許不是第一個會聯想到的詞,不過在原子層級,分子的物理與化學性質會受到量子力學交互作用的影響。例如,電子的自旋是一個基本量子特性,而電子自旋會影響電子所在分子的反應性,因此,每一個化學反應皆遵循量子理論的定律。
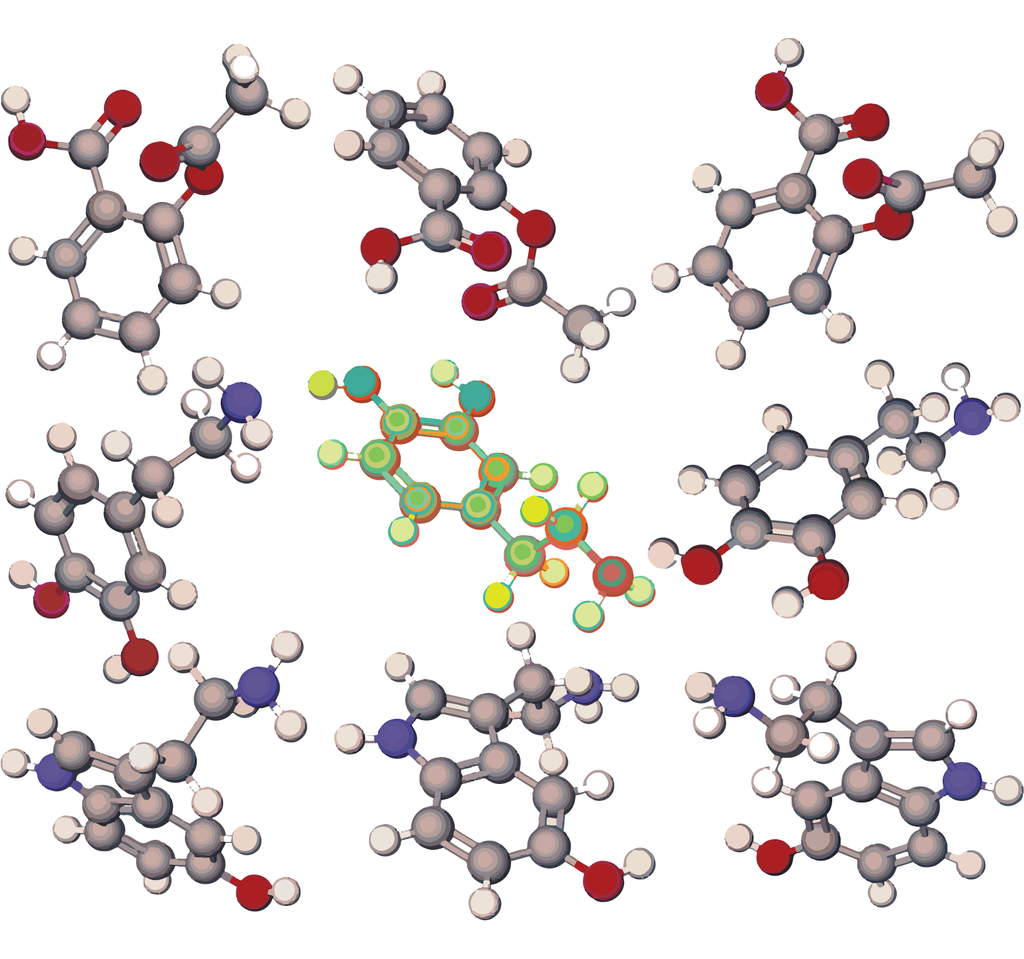
然而,量子性質的建模是困難的,因此對於需要了解此效應的產業,其研發成本非同一般。一個製藥公司平均花費24億美元研發一種新藥,絕大部分的成本用在臨床前研究(preclinical research)。由於化學家通常仰賴試誤(trial-and-error)過程來測試大約1000個小分子是否適用於臨床試驗,僅有約10%的臨床試驗能夠成功開發產品,所以許多化學公司尋求能夠提高分子建模的效率1,2。
計算化學領域的一個首要任務,是利用直接建模來取代目前的試誤方法,這種建模具有足夠精確度來分析所有的相關過程,像是室溫分子的反應速率等,有這樣的精確度,系統的行為可以被預測,成為量子化學一個關鍵基準。雖然許多方法可以在古典高性能電腦上模擬量子效應,但它們難以達到某些化學系統所需要的精確度,特別是對幾百或幾千個分子、具有強電子關聯或是耦合振動與電子關聯的大型系統。
不過,數十到數百分子的中型強關聯系統很快可以用量子電腦來分析,效率超過古典電腦(見圖1)。例如,一台約有100個防錯量子位元(error-protected qubits)的小型量子電腦,能夠計算約100個自旋軌道的能量,每個自旋軌道皆是一個能給出電子的位置與自旋的波函數3,4。這種功能對眾多應用很有用處,包括尋找適當的過渡金屬作為化學過程的有效催化劑。
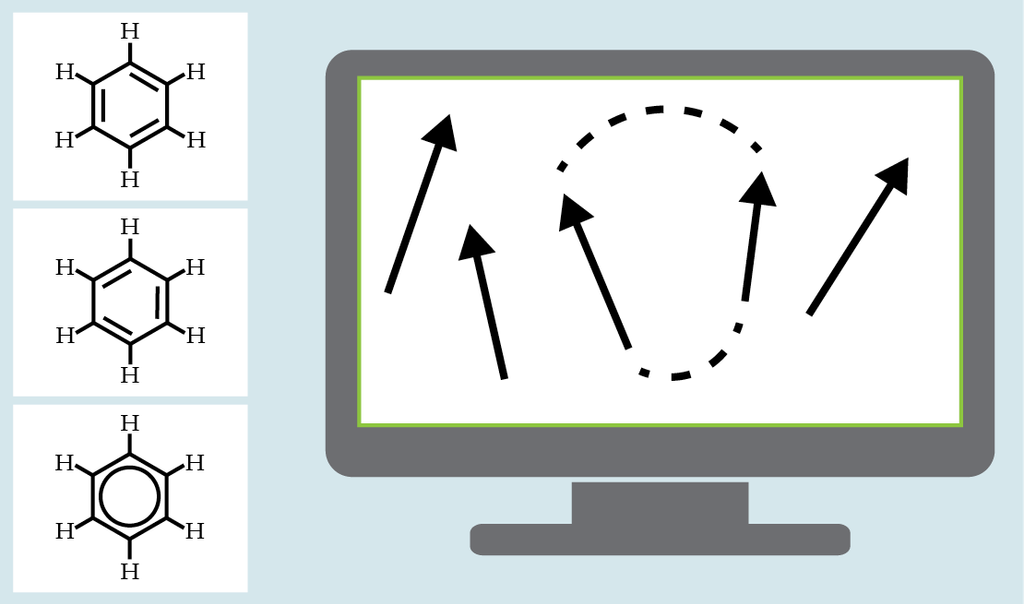
圖1、分子中的電子以量子力學來描述。像苯(benzene)這樣的分子相對簡單,其各種電子組態可用量子電腦的量子位元來表示,所取的值不僅是古典的0 (在這例子為自旋向上)和1(自旋向下),還有這些二元值的疊加 (在圖中標示為斜向自旋)。量子電腦本身為一個可控的量子系統,它的量子位元能夠被操控,並取出資料來產生模擬,未來目標是實現比古典電腦更精確的模擬。(Freddie Pagani製圖)
以Haber–Bosch過程為例,其用在製造化肥所需的氨已有超過100年的歷史,這個過程消耗了全世界約2%的能量。從長遠的角度來看,量子化學能夠模擬各種催化劑如何改進Haber–Bosch過程的氮還原反應與其它反應,使之更為節能。不過這種模擬現在還做不到,因為它需要大量的量子位元,Haber–Bosch過程一個抗錯(error-resilient)模擬需要約100萬個實體的量子位元。許多公司正努力建造更大量子位元數的量子電腦,甚至一些人誇口未來10年可達到100萬量子位元數的大關(見圖2)。
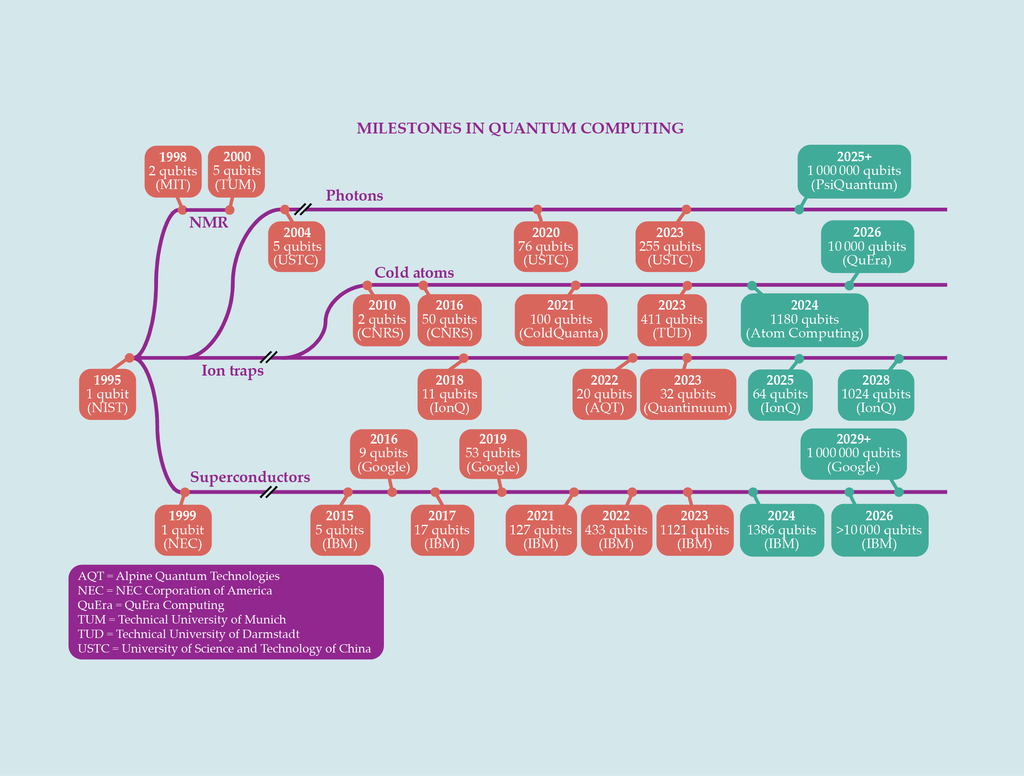
圖2、增加的量子位元數。雖然僅憑量子位元數不足以判斷一台量子電腦的性能,但許多研究發展已大幅提高了一台電腦所能承載的量子位元數。有了足夠的高品質量子位元,研究人員得以致力於一種「通用量子電腦」(universal quantum computer),能處理更多古典物理無法處理的計算。(Freddie Pagani製圖)
量子計算與量子演算法
化學的古典計算方法通常著眼於研究特定系統的勢能面(energy landscape)。化學系統的基態,也就是特定分子的最低能態,為分子中的所有原子核與電子之組態(configurations)的量子波函數。但要確定此基態,研究人員通常只調查所有可能組態的一小部分,因為有些分子態的量子疊加產生糾纏,導致完整組態太過龐大,無法在合理的時間內透過古典電腦來徹底分析。為了忽略其中許多組態而讓分析更容易處理,古典的計算演算法使用幾種近似,一些詳述於方框1中。
一些古典計算方法
為了模擬分子大量的電子組態,在某些情況下有幾種近似是有效的。以波恩–歐本海默近似(Born–Oppenheimer approximation)為例,它將分子的原子核和電子分開處理,因前者與後者的質量相差3個數量級,原子核可當作靜止點來分析,加速分子計算。這個近似看的不是電子的位置,而是它們一般被發現的組態(以所謂的自旋軌道)。
這個方法和其它方法可以幫助研究人員找到弱作用存在下化學系統的基態,但是大部分化學上有趣的系統,例如,有關化學鍵斷裂的強關聯系統,或是溶劑(solvation)化學的分散(dispersive)電子交互作用的系統,都是由表現高度糾纏的波函數所描述,在這些例子,波恩–歐本海默近似與其它類似的方法可能失效。
這些情況下的一種選擇,是透過一個稱為「精確對角化」(exact diagonalization)的程序來計算整個系統的能量。由於過去幾十年計算能力的快速成長,進行精確對角化的工具可以完整分析諸如氨之類的小分子,但對於較大的分子,比如說有10個電子分布在50個或更多的軌道,其組態太多超出現代電腦的能力。
除了分子基態,有限溫度內發生的動力學過程也是描述的重點。對於強關聯系統與數百原子的大型系統,計算相當困難,而近似法一般難以得到高精確度的結果,這些工具僅在量子效應可忽略的情況下有用,例如擴散計算和共形(conformal)過程的研究 (像是蛋白質摺疊等),但鑒於需要模擬的系統很大,這種計算預計不會太快在量子電腦上實現。
量子計算背後的基本想法,是將0或1的古典位元代換成可以以開和關的疊加態存在的量子位元。所有可能的量子態中,有些展現出獨特的量子特性:一個量子位元態的測量可能影響另一個量子位元態的測量之機率。在這情形下,量子位元是糾纏的,只要量子位元能抵抗雜訊,並且外部來源導致的誤差能得到修正,量子電腦的儲存容量就會呈指數性成長。因為2個量子位元可存在4種可能的疊加態,3量子位元可存在8個可能的疊加態,以此類推,n量子位元能用來儲存2n位元的資訊,一旦量子電腦約有60個量子位元,它的儲存容量很快超過古典電腦。
一些量子電腦的高度糾纏態可以有效描述主要由量子效應驅動的化學系統,這些系統可能缺乏古典的描述。事實上,量子電腦支援在根本上不同的計算和模擬方法,當量子電腦的應用比古典電腦更快速有效率時,即達到所謂的「量子優勢」(quantum advantage)(更多有關量子電腦的設計,請參閱Anne Matsuura、Sonika Johri與 Justin Hogaboam在Physics Today的文章,2019年三月號第40頁;還有Harrison Ball、Michael Biercuk 與Michael Hush的文章, Physics Today, 2021年3月第28頁)。
對古典電腦來說,運算是透過邏輯閘進行,邏輯閘利用1個或多個二位元輸入來產生單個二位元輸出;而量子電腦的工作原理類似,但是使用量子邏輯閘。未來的化學系統模擬,可透過模擬中將各個操作分解成通用量子計算邏輯閘組的元素來完成,利用這個方法,多個模擬可以在同一台電腦上進行。
然而,這方法需要大量的量子位元及其它計算資源,考慮到要執行的邏輯運算次數,此方法增加了雜訊敏感度(noise sensitivity)與計算誤差的風險。確實,量子閘要如何忠實地在實際設備上執行,仍然是量子計算的關鍵挑戰,各種因素,包括量子位元與環境之間不受歡迎的作用,以及不完善的量子位元控制,都會降低運算效能。
防範的做法像是創造儲存資訊的多個副本等,已經專適用於量子電腦,並稱作為「量子除錯」(quantum error correction)。儘管這方法亦需要大量的量子位元――早年估計利用1000個量子位元獲得一個防錯(error-protected)量子位元――但糾錯的創新工作正快速發展,近期在錯誤控制方面的突破5-7,有潛力迎來容錯量子計算(fault-tolerant quantum computing,FTQC)的時代,屆時量子電腦將可程式化並且結果可信,如同今日的古典電腦。事實上,有跡象顯示我們正過渡到FTQC時代8,對所有業界而言,特別是化學領域,最有趣的時刻將會是大型容錯量子電腦能充分利用量子優勢的時候。
目前業界正處於雜訊中等規模量子(noisy intermediate-scale quantum,NISQ)時代,NISQ設備能夠執行邏輯閘的演算法,但精度有限,不過我們可以避開邏輯閘方法轉向要求較低的類比量子模擬。分子動力學模擬或其它方法可繞過閘分解,直接模擬有興趣的真實系統的時間演化,此種方法在NISQ時代能否實現量子優勢,目前正在研究中。
無論選擇哪種方法,推動量子計算(特別是化學)的關鍵要素,是持續發展結合量子資訊理論與古典技術的量子演算法,因n量子位元的量子電腦能同時操控與儲存2n 位元的資訊,量子演算法的運作方式和古典電腦演算法可能相當不同。不過,這種演算法仍處在起步的階段,且這領域還未收斂到一種可以保證量子優勢的單一方式。圖3列出了當前模擬量子化學問題有希望的演算法,清單很長,突顯為量子化學模擬的下一階段,理論方面已經有許多工作完成。有關一些具體方法的詳情,請見方框2。
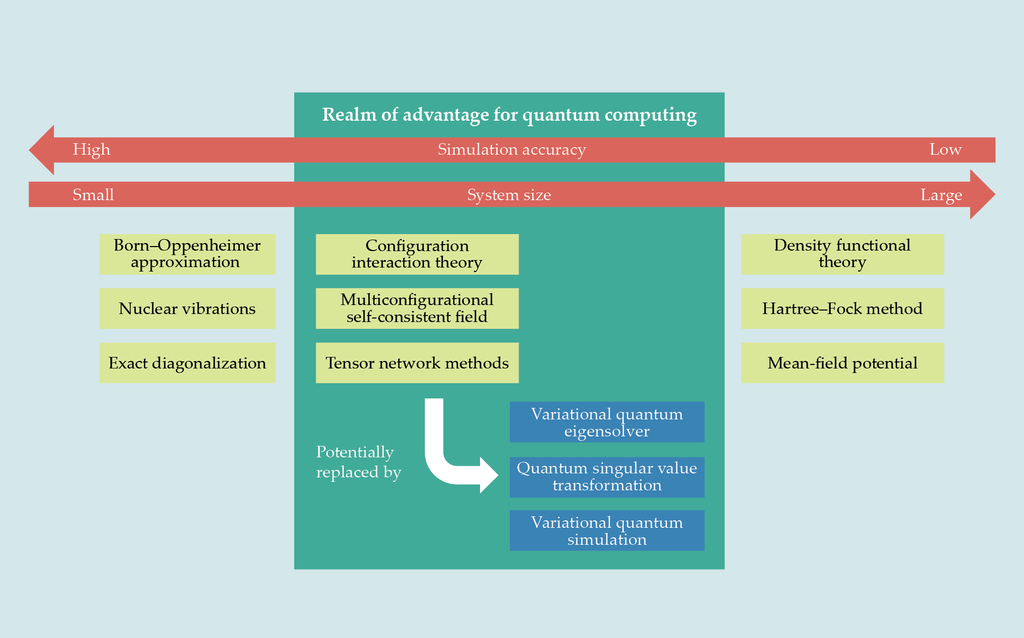
圖3、優勢領域。幾種古典計算方法可模擬量子系統,但精確度隨著系統大小增加(紅色箭頭)而減小。對於數十到數百分子的中型化學系統,量子電腦上運行的新興量子演算法能取代一些古典方法,更高效地模擬某些化學系統。(Freddie Pagani製圖)
量子計算演算法
一些已開發的量子計算演算法常為現有古典方法的延伸。長期以來,人們對於一種稱為「變分量子本徵求解器」(variational quantum eigensolver,VQE)的演算法寄予厚望,希望它能處理像是尋找化學系統基態等問題18。VQE的設計結合了古典與量子的計算方法,此種混合方式更好用,因為它避免長時間的運算 (增加今日易錯量子電腦的錯誤率),並能善用今日高效能古典電腦的強大功能。
藉由古典與量子處理器之間的轉換,這混合式演算法最後以下述方法來訓練量子電腦:VQE將自由控制參數引入特定的量子演算法,接著執行該演算法來準備所需的基態,從讀取終態並測量其能量的結果拿來更新控制參數,經過幾次迭代,控制參數預期會收斂到一個能精確產生基態的最佳化組合。因為這個最佳化程序,VQE能夠採取簡單的演算法,而達到比當今其它量子方法更高的準確度。然而,這最佳化程序隨著系統大小呈指數性增長,所以VQE可能不適用在超過100個實體量子位元的量子電腦。
但量子化學演算法要算的不僅僅是系統能量。例如尋找各種反應的催化劑(包括產生氨的Haber–Bosch過程)還需要仔細研究分子如何隨時間彼此反應,這無法以標準VQE演算法來簡單實現,人們開發了許多方法來對有興趣之特定系統進行時間模擬3,其中兩個著名的例子為Trotterization與變分(variational)量子模擬。
Trotterization將化學反應的時間演化分解成很多個微小步驟,使系統的交互作用可用許多量子閘操作來表示,目前這個程序因量子閘精確度的不足,而有所限制;相比之下,變分量子模擬則如同VQE仰賴控制參數,模擬測試態的短時間演化之演算法,最佳化能收斂到一個適當的化學系統總能量結構的表示,此最佳化演算法可用來模擬Hilbert空間中複雜狀態的長時間演化,而最後產出有用的動力學量,像是粒子相關函數,揭示系統所處的物質相。
硬體
隨著許多演算法的到位及開發,渴望利用預期量子優勢的業界,將注意力轉向硬體供應商,以及何時得到足夠信賴之量子計算設備的時程問題。幾家公司仰賴各樣技術平台,包括自旋量子位元、拓樸系統與光子量子計算等,來開發量子電腦。勝利之道也許涉及幾種技術的整合,市場可能會循者贏者通吃(winner-takes-all)的心態,不過目前,所有這些技術都在考慮之中。
我們的目的是開發一個能夠執行所有可能量子演算法的通用設備,為了成功,任何正在研究的平台都需要解決幾個問題。根據產業界的主流意見,有兩項技術大有可為:原子阱(trapped atoms)9,10與超導量子位元11 (見圖4的概述) 。
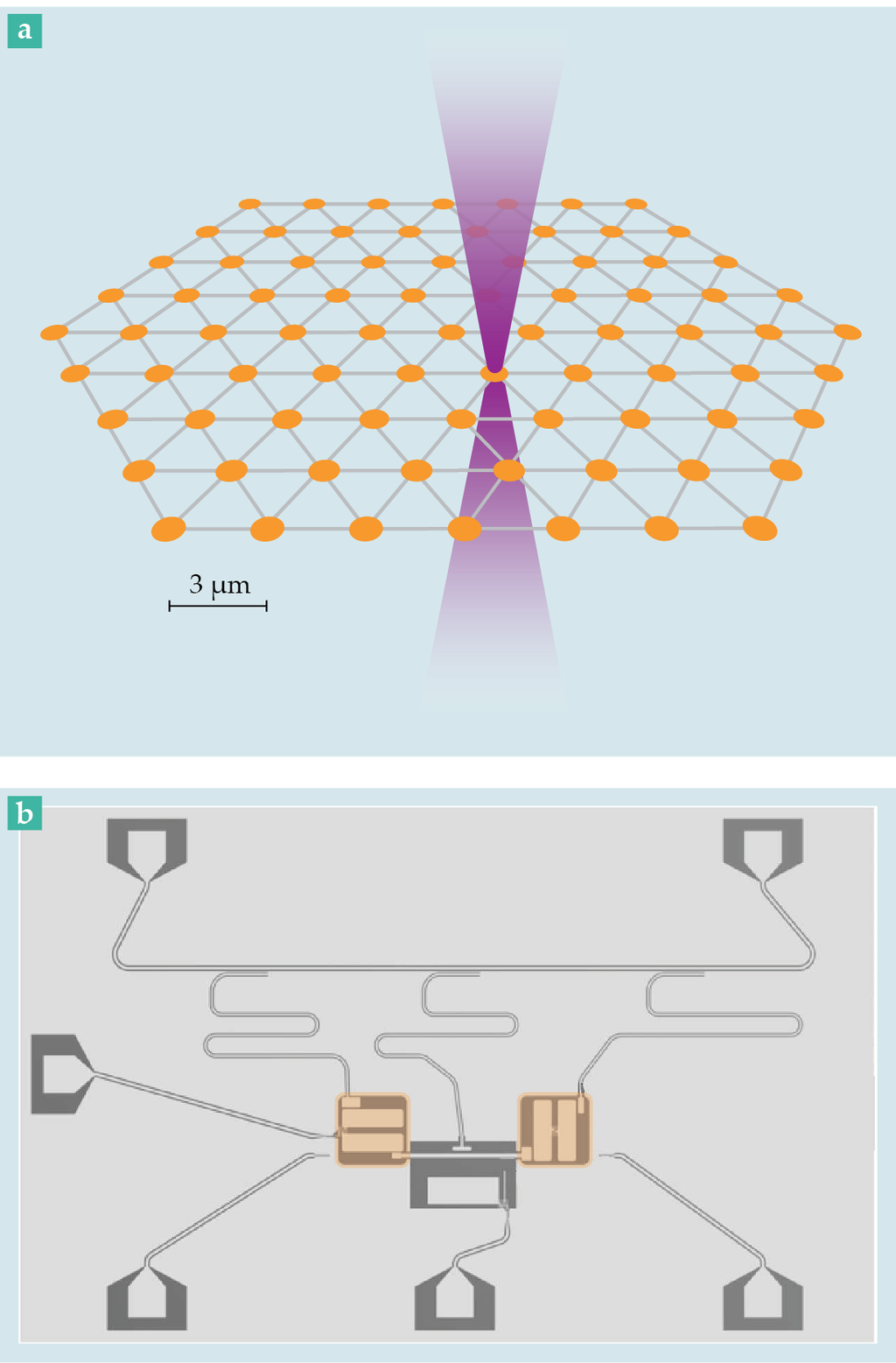
圖4、兩種量子電腦。(a) 被捕獲於真空胞中光學鑷夾陣列的冷原子,可作為量子電腦中的量子位元,小束(beamlets)與反射鏡將雷射光聚焦在量子位元上,所產生的交互作用如同可執行邏輯功能的量子閘(改編自參考文獻9)。(b)電路中包含超導材料(可形成量子位元,以橘色強調)可轉變成量子電腦,電磁訊號透過電路導線發送來執行量子閘與讀取量子位元的狀態。(圖片提供:Walther Meissner Institute)
雷射冷卻技術是研究人員最先使用的方法之一,其將原子個別捕獲後使之冷卻至低於 1 mK 的溫度。當原子被游離時,會被電場困住;對於中性粒子,光學鑷夾則能將它們限制在其中。這兩個方法中,當兩個能階(通常為基態和某種激發態)透過電磁輻射耦合,會形成一個量子位元,結果為一個單量子位元量子閘。如果原子是透過靜電力(對於囚禁離子)或凡德瓦/電偶極交互作用(對於中性原子)作用而被捕獲在陷阱中,會形成雙量子位元量子閘。
近幾年來,限制於光學鑷夾的1、2維中性原子陣列已展示高精確度的多量子位元運算,並成為量子模擬與計算的一個強大平台。此方法中,當原子被激發到雷德堡態(Rydberg states,具有很大的主量子數與大空間範圍的高能態)時,相鄰鑷夾的原子之間產生可控的強作用力。
雷德堡原子作為平台的關鍵優勢是它們已被證明的可擴縮性(scalability),這種系統裡,量子位元數的範圍可從數百到數千不等。藉由動態重組雷德堡原子陣列,研究人員能為各類型的量子閘設計任意的晶格幾何形狀及連接方式,接著,利用高靈敏CCD相機和微米解析度的影像系統來拍攝單原子螢光影像以讀取量子位元。重組原子陣列的技術將促進未來幾年FTQC時代的發展。
對於演算法的應用,一項主要挑戰是量子閘精確度因技術缺陷和導致去同調的物理效應而受到限制,不過,最近的突破性實驗展示了卓越的技術成就,包括精確度99.5%的雙量子位元閘運算,還有數十個邏輯量子位元進行邏輯運算時的誤差壓抑8,邏輯量子位元本身由許多實體量子位元所組成。
另一個有希望的技術平台「超導量子電路」,則採取與原子不同的方式來發展量子位元。超導平台類似古典的計算結構,電路在矽晶片上奈米製程,其組成為諸如電感與電容等古典元件,但除此之外,電路整合了超導元件,即所謂的約瑟夫森接面(Josephson junctions)。有了這些接面,電路就像一個量子位元,展現基態與激發態之間的躍遷頻率,一般介於300 MHz與5 GHz間,取決於超導電路的精確設計與結構。由於各個超導量子電路是單獨製程,它們通常也被稱為人造原子,它們為可能的量子位元性質提供豐富的參數空間,以及提供可預測效能的操作狀態。
許多業者已製造出數百超導量子位元的大型設備,且雙量子位元閘的精確度峰值達99.9%。然而,這些電路需要昂貴、複雜的奈米製程技術來達到最佳的結果;另一個限制是,超導量子位元和其它任何量子位元一樣,容易受到雜訊的影響:例如溫度擾動可能導致量子位元被激發到較高能階,而在計算中引入誤差。因此,任何的超導量子處理器單元都需要在大約10 mK 的低溫操作。(更多關於超導量子位元的除錯,請參閱José Aumentado、Gianluigi Catelani與 Kyle Serniak在Physics Today的文章, 2023年八月號第34頁。)
現代致冷器(cryostats)是可能達到如此低溫,不過假使系統擴展到大數量的量子位元,它們的維護就非常棘手。每一個量子位元是透過專門的線路來控制與讀取,這條線路連接量子處理器與致冷器外部的控制軟體,要利用數千條纜線單獨處理每個量子位元,是很大的佈線考驗,因為如此密集的接線安排會導致不必要的熱輻射干擾量子位元。因此,這個領域出現若干降低接線複雜性的想法,像是相同的線路用在多個量子位元,稱為多工(multiplexing),還有使用低溫下工作的控制電子元件。
雖然幾乎所有的平台都有這些和更多的技術挑戰,但現有的原型(prototypes)已經證明,冷原子技術與超導電路在原則上是可行的,幾家公司正研究減少誤差的策略,並在超導與原子阱平台上進行邏輯量子位元的編碼12,甚至化學系統的應用已展示在20個量子位元的超導量子電腦上13,這個成就使其成為目前為止量子化學在量子電腦上的最大模擬。隨著原理證明的達成,現在的核心問題為,”要縮小與現實生活使用案例(use cases)的差距,還需要什麼步驟?而誰會完成它們呢?”
MOQS聯盟
量子化學的量子計算仍面臨著許多挑戰,特別是高誤差率及現有硬體的低量子位元數,要建構強大的量子處理器單元並確定適當的演算法,需要龐大的技術研發。推動此一發展最著名的公司為Google、Microsoft及IBM等美國科技巨頭,而全世界也湧現超過100家量子新創公司。
歐盟的量子產業正在快速成長,主要是學術的領域,根據麥肯錫公司(McKinsey & Company)於2023年四月的分析,歐盟在量子技術相關的領域培養最多的碩士生,約有135000人。 為了使新的知識領袖與新興量子產業產生連繫,展望歐洲(Horizon Europe)計畫資助了「歐洲分子量子模擬培訓網路」(European Training Network for Molecular Quantum Simulations,MOQS)的計畫。
MOQS聯盟由歐盟的幾家公司與研究單位組成,借助他們的專業,聯盟每年訓練15位實驗物理與理論化學等多個學門的博士生。除了尋找高效率的量子演算法和處理技術難題,MOQS成員也致力於量子計算研究前沿的一系列課題,在某些情況下,他們已突破了新的概念基礎。
譬如說,在瑞士蘇黎世的IBM 研究院(IBM Research),MOQS成員研究邏輯值0與1為計算基底(computational basis)的常用測量之替代方式。正算符值測量(positive operator-valued measurement,POVM)對計算算符的期望值具有優勢,這在許多量子演算法中是重要的,但這些測量被認為需要額外的量子位元,使它們的實現更加困難且需要更多的資源。新的MOQS成果顯示,正算符值測量可在現有的超導量子計算平台上有效實行,而不需要額外的量子位元14。
在荷蘭埃因霍溫理工大學(Eindhoven University of Technology)與法國的史特拉斯堡大學(University of Strasbourg),MOQS成員研究基於交互作用雷德堡原子的量子邏輯閘,他們研發的最佳化雷射脈衝15應可能達到超過99.9%的量子閘精確度,最近剛證明達到99.5%16。除此之外,斯洛維尼亞盧比雅那的新成果,正協助揭開交互作用量子多體系統的複雜動力學17。
與業界的緊密連繫,能進一步保證MOQS的博士生獲得推動量子化學領域前進的必要技能;主要公司包括 BASF、HQS Quantum Simulations 與 Bosch等加入聯盟,亦確保研究計畫能帶給產業可應用的使用案例。只有這樣的緊密配合,才能縮短預期實現量子優勢的時間。
早期採用
化學產業對量子計算的興趣,源自於希望量子方法能協助以更低成本、更少時間開發更好的新產品,儘管如此,在量子電腦創造真正的效益以前,企業很可能還得等待幾年。如前面所提,在100-量子位元的量子電腦上模擬100個自旋軌道的分子是可能的,但即便如此,還是遠不及製藥公司的長期目標:當他們透過量子模擬設計新的藥物與材料時,有95%的批准藥物分子是大於200自旋軌道系統3。
另一個考慮的因子是除錯,多達1000個實體量子位元組合起來產生單個抗錯邏輯量子位元,只有存在抗錯量子位元時,演算法才能正常運作,並且提供比古典演算法更快的量子加速。近期有許多新的進展顯示如何在幾百量子位元的量子設備上實現除錯8,因此,這領域可能比預期的更快超越NISQ時代。
我們三個希望化學產業在這10年底能看到計算上的量子優勢——或,假如技術以目前驚人的速度發展的話,也許會更早。此外,分子建模不是唯一量子效應有用途的領域,雖然化學產業首先看到了先機,但量子計算將影響其它許多種產業,包括設計與開發催化劑與新的材料、電池、半導體、磁鐵,以及高溫超導體等。
我們感謝Daniel Bultrini 與 Christoph Hohmann幫忙圖片與圖形表示,亦感謝歐盟Horizon 2020研究與創新計劃 (補助編號955479)的分子量子模擬(MOQS)聯盟提供有價值的意見及協助。
References
1.F. Budde, D. Volz, “The Next Big Thing? Quantum Computing’s Potential Impact on Chemicals,” McKinsey & Company (12 July 2019).Google Scholar
2.P. Gerbert, F. Ruess, “The Next Decade in Quantum Computing—and How to Play,” Boston Consulting Group (15 November 2018).Google Scholar
3.S. McArdle et al., Rev. Mod. Phys. 92, 015003 (2020). https://doi.org/10.1103/RevModPhys.92.015003Google ScholarCrossref OpenURL
4.Y. Cao et al., Chem. Rev. 119, 10856 (2019). https://doi.org/10.1021/acs.chemrev.8b00803Google ScholarCrossref OpenURL PubMed
5.U. Réglade et al., Nature 629, 778 (2024). https://doi.org/10.1038/s41586-024-07294-3Google ScholarCrossref OpenURL PubMed
6.S. Ma et al., Nature 622, 279 (2023). https://doi.org/10.1038/s41586-023-06438-1Google ScholarCrossref OpenURL PubMed
7.S. Bravyi et al., Nature 627, 778 (2024). https://doi.org/10.1038/s41586-024-07107-7Google ScholarCrossref OpenURL PubMed
8.D. Bluvstein et al., Nature 626, 58 (2024). https://doi.org/10.1038/s41586-023-06927-3Google ScholarCrossref OpenURL PubMed
9.M. Morgado, S. Whitlock, AVS Quantum Sci. 3, 023501 (2021). https://doi.org/10.1116/5.0036562Google ScholarCrossref OpenURL
10.J. I. Cirac, P. Zoller, Phys. Rev. Lett. 74, 4091 (1995). https://doi.org/10.1103/PhysRevLett.74.4091Google ScholarCrossref OpenURL PubMed
11.P. Krantz et al., Appl. Phys. Rev. 6, 021318 (2019). https://doi.org/10.1063/1.5089550Google ScholarCrossref OpenURL
12.Y. Kim et al., Nat. Phys. 19, 752 (2023). https://doi.org/10.1038/s41567-022-01914-3Google ScholarCrossref OpenURL
13.Google Quantum AI, Nature 614, 676 (2023); https://doi.org/10.1038/s41586-022-05434-1Crossref OpenURL [PubMed]
T. E. O’Brien et al., Nat. Phys. 19, 1787 (2023). https://doi.org/10.1038/s41567-023-02240-yCrossref OpenURL Google Scholar
14.L. E. Fischer et al., Phys. Rev. Res. 4, 033027 (2022). https://doi.org/10.1103/PhysRevResearch.4.033027Google ScholarCrossref OpenURL
15.S. Jandura, G. Pupillo, Quantum 6, 712 (2022); https://doi.org/10.22331/q-2022-05-13-712Crossref OpenURL Google Scholar
M. Mohan, R. de Keijzer, S. Kokkelmans, Phys. Rev. Res. 5, 033052 (2023). https://doi.org/10.1103/PhysRevResearch.5.033052Crossref OpenURL Google Scholar
16.S. J. Evered et al., Nature 622, 268 (2023). https://doi.org/10.1038/s41586-023-06481-yGoogle ScholarCrossref OpenURL PubMed
17.Y. Kasim, T. Prosen, J. Phys. A 56, 025003 (2023). https://doi.org/10.1088/1751-8121/acb1e0Google ScholarCrossref OpenURL
18.N. Moll et al., Quantum Sci. Technol. 3, 030503 (2018). https://doi.org/10.1088/2058-9565/aab822Google ScholarCrossref OpenURL
19.A. Matsuura, S. Johri, J. Hogaboam, Phys. Today 72(3), 40 (2019). https://doi.org/10.1063/PT.3.4163Google ScholarCrossref OpenURL
20.H. Ball, M. J. Biercuk, M. R. Hush, Phys. Today 74(3), 28 (2021). https://doi.org/10.1063/PT.3.4698Google ScholarCrossref OpenURL
21.J. Aumentado, G. Catelani, K. Serniak, Phys. Today 76(8), 34 (2023). https://doi.org/10.1063/PT.3.5291Google ScholarCrossref OpenURL
Klaus Liegener 是慕尼黑邁斯納研究所的量子物理學家;Oliver Morsch 是佛羅倫斯國家光學研究所的研究主任,身兼比薩大學的量子科技教授,都在義大利;Guido Pupillo是法國史特拉斯堡大學的量子物理教授。
本文感謝Physics Today (American Institute of Physics) 同意物理雙月刊進行中文翻譯並授權刊登。原文刊登並收錄於Physics Today, Sep. 2024雜誌內 (Physics Today 77 (9), 34–42 (2024); https://doi.org/10.1063/pt.qoys.tiuw )。原文作者:Klaus Liegener; Oliver Morsch; Guido Pupillo。中文編譯:張鳳吟,國立陽明交通大學物理學系博士。
Physics Bimonthly (The Physics Society of Taiwan) appreciates Physics Today (American Institute of Physics) authorizing Physics Bimonthly to translate and reprint in Mandarin. The article is contributed by Klaus Liegener; Oliver Morsch; Guido Pupillo and was published in (Physics Today 77 (9), 34–42 (2024); https://doi.org/10.1063/pt.qoys.tiuw ). The article in Mandarin is translated and edited by F. Y, Chang, National Yang Ming Chiao Tung University.

