在實現光學神經網絡的道路上，顛覆資料編碼的方式可以移除巨大的絆腳石。

人工神經網路不僅正在改變世界，也對全球的能源消耗產生影響。一般大眾和科學界使用的機器學習應用所仰賴的這些由大腦構造所啟發的運算模型，其能力已被證明十分強大（參見《今日物理》，2021年10月，第14頁）。然而，它們的耗能也非常驚人（參見《今日物理》，2024年4月，第28頁）。

減輕能源負擔的一種潛在方法是設計一種以光而非電子來處理資料的電腦。人工神經網路所需的絕大多數運算是線性的，例如加法、減法以及乘以常數。光學電腦可以快速且高效地執行這些操作。

儘管光學計算在處理線性運算方面表現出色，它在處理非線性運算時卻面臨巨大挑戰。非線性運算是人工神經網路計算中佔比不大但不可或缺的一部分，它對光學電腦帶來挑戰的根本原因在於光子通常不會彼此交互作用。一些非線性光學材料可以媒合光與光的相互作用，從而產生非線性響應，但這通常需要高得不切實際的光功率。

上述的思維假設了資訊被編碼在光場中，然後由光學神經網路進行處理與操作。不過，目前已有三個研究小組證明了這並非唯一可行的方式。雖然這些小組的做法各不相同，但他們同樣都想到了：將輸入資料編碼在和光交互作用的某個系統，而非直接編碼於光本身。如此一來，非線性函數的計算變得更為容易，而人工神經網路的實現也將水到渠成。

在德國埃爾朗根的馬克斯‧普朗克光學研究所，克萊拉·萬朱拉（Clara　Wanjura）和弗洛里安·馬庫亞特（Florian Marquardt）從理論上證明，輸入資料可以表示為耦合諧振器系統中的頻率偏移[1]。另一個由耶魯大學的曹蕙（Cao Hui）和巴黎高等師範學院的席爾凡·及剛（Sylvain Gigan）領導的團隊[2]，以及由瑞士洛桑聯邦理工學院（EPFL）的德米特里·普薩爾提斯（Demetri Psaltis）和 克里斯多夫·莫瑟（Christophe Moser）領導的團隊[3]，則從實驗方面將資料編碼於多次散射的光的像素陣列中。在這些案例中，光學系統在處理基礎影像分類任務時，能夠表現出和數位神經網路相當的準確率。

 

資料處理的曙光

神經網路其實就是一個複雜的數學函數。它接收一個輸入，例如圖1插圖中顯示的手寫數字的模糊影像，並產生一個輸出：「7」。為了將輸入轉換為輸出，神經網路會將數據經過多層節點（或稱為神經元）進行處理。

圖一.受大腦的啟發，人工神經網絡透過在多層節點（神經元）之間傳遞訊息來處理資訊。在此過程中，會有可訓練參數的矩陣（如插圖中標示的 J1 和 J2），這些參數經過來回調整，以最佳化網絡執行特定任務。在本圖中，任務內容是辨識數字圖像。（圖片由克萊拉·萬朱拉提供；插圖改編自參考資料1。）

在傳統的神經網絡中，每個神經元會計算所有輸入資料的加權平均值。接著，根據結果是否超過某個門檻值，神經元要麼觸發（輸出 1），要麼不觸發（輸出 0），並將輸出傳遞至下一層。這些加權平均值中使用的權重即所謂的訓練參數：模型透過一系列已知正確輸出的輸入來反覆調整，直到最終能正確處理未曾見過的輸入。

即使在訓練階段，這些加權平均運算也消耗了大部分的計算資源，而這類線性運算正是光學計算的強項。將兩個光學信號相加就只要把兩個光場疊加起來就好。而即使是一系列更複雜的加權總和，也能利用分束器和相位移器系統輕鬆完成[4]。

在進行線性運算時，光學計算的表現優於電子計算，原因就和光纖在長距離傳輸上的優勢同理：編碼在光束中的資訊可以在空間和時間上高度壓縮，且能以極小的耗損長距離傳輸。因此，數據能以高吞吐量和低功耗方式進行處理。

然而，光學神經網絡面臨的最大挑戰是運算中聽起來最簡單的部分：每個神經元是否觸發的決定，這是一個輸入訊號的非線性函數。雖然可以用非線性光學計算，但需要高功率光學，或者將信號在光學和電子之間轉換，但這些方法會抹除光學計算的一些主要優勢。

值得慶幸的是，神經網絡對非線性函數的性質並不太挑剔。它不一定必須是全有或全無的階梯函數。事實上，多數應用為了計算方便，採用的是平滑的階梯函數，而如果經過適當訓練，許多其他非線性函數也能發揮作用。因此，問題變成了：一個完全由線性光學組成的平台能否模擬出任何非線性函數？

 

House of mirrors鏡之屋

這個問題的答案——響亮的「是」——取決於是否問出正確的第二個問題：「什麼的非線性函數？」 按定義，線性光學只能計算輸入光場的線性函數，但它可以對其他物理參數（例如鏡子的位移）產生非線性響應。不過，要將這些非線性性質作為神經網絡的基礎，需要對網絡結構進行重大調整。

耶魯大學的Cao及其團隊研究光學非線性現象時，原本目的是應用於另一個領域：並非神經網絡，而是希望創建一種「實體不可複製函數（Physical Unclonable Function, PUF）」，這是一種數位指紋，可以在物聯網中作為安全特徵[5]。他們設計了一個高爾夫球大小的球形腔體，如圖 2a 所示，腔體內的部分表面覆蓋了一層可重新排列的小型反射鏡陣列，其餘表面塗上漫反射塗層。當雷射光束從腔體上的一個孔射入時，光線會在腔體內多次反射，最終從另一個孔射出，呈現某種斑點圖案。

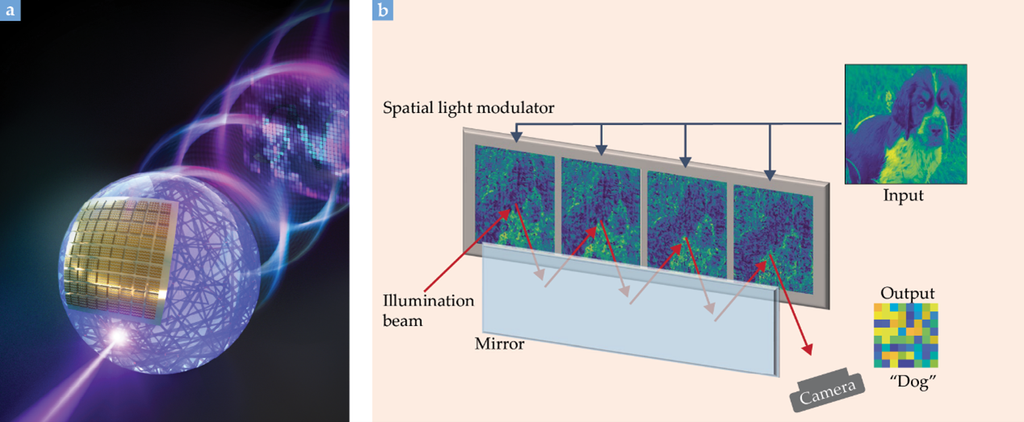圖2.為了以光作為神經網絡的基礎，研究人員必須重新思考如何編碼和處理資料。(a) 一個球形腔體，部分內壁貼有可重組反射鏡陣列，當光在腔體內反射後，會產生看似隨機的斑點圖案。然而，這些斑點卻攜帶了鏡子陣列中編碼圖像的詳細資訊。（圖片由 Fei Xia 提供。）(b) 在另一個較可程式化的應用中，輸入圖像的四個副本被編碼到空間光調變器（spatial light modulator）中。一道光束照射這四張圖後產生散射。該系統可以被訓練來分類圖像，即使是它以前從未見過的圖像。（改編自參考資料 3。）

 

輸出的斑點圖案取決於鏡子配置的方式，並且是以決定性和可重現的方式生成，但沒有這個腔體幾乎不可能複製該圖案。這些特性使該系統成為一種實體不可複製函數（PUF）。但這也是一個神經網絡嗎？乍看之下似乎並非如此：它沒有明顯的神經元、加權平均或可訓練參數。然而，Cao的團隊在與Gigan和其博士後 Fei Xia 合作時，發現這個腔體可以做為所謂的「儲備池電腦」，這是一種神經網絡，先完成所有計算，之後再進行詮釋。

斑點圖案是鏡子配置的高度非線性函數。研究人員估算，光平均在腔體表面反射數千次後才射出，其中至少幾百次反射是發生在鏡子陣列上。產生的斑點富含輸入資料中像素間的相關性資訊，而相關性正是所有神經網絡能夠展現妙用的核心元素。

為了解讀斑點圖案，研究人員只需將其通過一個含有一或多層可訓練權重的解碼器，這在電子上相對簡單。擁有超過四百萬像素的鏡子陣列可以編碼極其詳細的輸入圖像，而該系統能執行一些複雜的計算任務，包括識別人臉的微妙特徵以及在交通場景中辨認行人。這些任務需要解碼器中多達一百萬個可訓練參數，然而相比傳統神經網絡，完成相同任務所需的參數要少得多。

瑞士聯邦理工學院的研究人員同樣受到了Cao及其團隊 PUF 論文的啟發，但他們的實現方式與之不同。「我們希望保留一定程度的可程式化能力，」該論文的共同第一作者 Mustafa Yildirim（與 Niyazi Ulas Dinç）表示。與Cao和Gigan 的合作團隊類似，EPFL 團隊透過讓光束在輸入圖像上多次反射來產生非線性。然而，他們不是讓散射隨機進行，而是控制光以之字形路徑行進，並在空間光調變器上與輸入圖像的四個不同副本進行散射，如圖 2b 所示。

這四個輸入副本並非完全相同。在每個副本中，每個像素都由一對可訓練參數線性縮放，因此研究人員可以像傳統神經網絡一樣訓練他們的系統。雖然光只在輸入圖案上反射四次，但非線性程度已足夠讓 EPFL 團隊成功訓練系統執行簡單的圖像分類任務，例如區分狗、魚和 T 恤的圖片。另外由於輸入資料被編碼了四次，該網絡有相當好的抗噪性能。

 

全新架構

Wanjura 和 Marquardt 的研究在這三個團隊中最為抽象。作為理論學者，他們專注於神經形態計算方式背後的數學概念。「我以前在研究拓撲學時使用過散射理論，」Wanjura 表示。「當我閱讀 Florian Marquardt 關於機器學習的講義時，注意到我研究過的散射矩陣與神經網絡背後的數學有一些相似性。所以當我以博士後身份加入他的團隊後，我們便共同進一步發展這個想法。」

與傳統神經網絡類似，Wanjura 和 Marquardt 設想的網絡由離散神經元組成。但不同的是，資訊在網絡中不僅僅是單向流動。光波（或任何形式的波）在網絡中以雙向方式來回散射。由於輸入資料和可訓練參數被編碼進某些神經元中，因此光信號對這兩者產生了非線性關係。

他們提出：這樣的網絡可以由一個耦合諧振器系統來實現，透過將諧振器調離共振點來進行資訊編碼。目前，他們正與史丹佛大學的 Amir Safavi-Naeini 帶領的實驗團隊合作，將這個想法化為現實。它們的第一步是在普通電腦上模擬這個網絡，以驗證它能夠將手寫數字圖像進行分類。「這很諷刺，」Wanjura 說道，「在電腦上模擬訓練過程需要幾個小時，而光子學實驗在理想情況下可以在幾毫秒內完成整個訓練。」

這三個團隊的研究仍處於概念驗證（proof-of-principle）階段。由於他們的網絡處理數據的方式與傳統神經網絡截然不同，目前尚不清楚它們能否規模化到與執行應用（如 ChatGPT）的強大但耗電的硬體分庭抗禮。然而，這些概念實現表明了跳出框架思考具有潛在的價值。「這激勵了我們在光學計算領域中更願意冒險，」Dinç 表示，「而不只是從電子計算直接複製貼上。」

 

本文感謝Physics Today (American Institute of Physics) 同意物理雙月刊進行中文翻譯並授權刊登。原文刊登並收錄於Physics Today, Aug. 2024雜誌內(Physics Today 77 (10), 12–14 (2024);https://doi.org/10.1063/pt.vbbo.lurd )。原文作者：Johanna L. Miller。中文編譯：林祉均。

Physics Bimonthly (The Physics Society of Taiwan) appreciates Physics Today (American Institute of Physics) authorizing Physics Bimonthly to translate and reprint in Mandarin. The article is contributed by ohanna L. Miller and was published in (Physics Today 77 (10), 12–14 (2024);https://doi.org/10.1063/pt.vbbo.lurd).The article in Mandarin is translated and edited by J.R Lin.