我和約翰·貝爾有過成功的合作，和一段溫暖的友誼。他最為人所知的是對量子力學基礎所作的重要工作，不過他也對粒子物理和加速器物理做也有卓越貢獻。
我和約翰·斯圖爾特·貝爾是在歐洲核子研究組織（CERN）理論部門的休息室裡喝茶時認識的。我在1978年4月抵達那裡，當時我是一名奧地利研究員。在每周一次的理論研討會結束後，該部門為所有新成員舉辦了一場歡迎會。約翰是一位令人印象深刻的人，比我大17歲左右，戴著金屬框眼鏡，紅髮，留著鬍鬚。他問起我的研究領域，當我回答「夸克偶素」時，他表現出極大的興趣。我們立即在他的辦公室展開了一場熱烈的討論——從此開啟了一段成功的合作和溫暖的友誼。
夥伴
夸克偶素就好比正子電子偶，指的是由夸克和反夸克組成的束縛系統。此類狀態在強子（含夸克的粒子）相互作用後獲得的能量光譜中呈現一個窄峰；因此，夸克子狀態常被稱為共振態。在 20 世紀 70 年代，粒子物理學家發現了幾種這樣的共振態，包括 J/ψ（由魅夸克和反魅夸克組成的束縛態）和 ϒ（由底夸克和反底夸克組成的束縛態）。這些粒子的性質需要被理解，因此當約翰和我第一次合作時，夸克偶素是一個熱門的研究領域。
當時，物理學家們意識到，僅考慮短距離夸克相互作用就能取得相當大的進展。例如，可以準確預測共振態的壽命[1]。 然而，約翰和我希望理解共振態的位置；為此，我們必須納入長距離相互作用，這大大增加了計算的複雜性。首先，我們必須考慮與膠子（類似於光子的粒子）之間的相互作用，這些膠子傳遞強交互作用力，將夸克束縛在一起。這使得我們必須超越微擾理論，納入所謂的膠子凝聚態：量子色動力學真空中的膠子波動。
我們的做法是透過一種稱為位能理論的近似方法來近似完整的量子場論，當時這是一種相當流行的模型。在這個框架內，我們成功地獲得了J/ψ和ϒ共振態的基態能量，誤差在10%左右，不過我們沒有能夠在位能理論與完整的量子理論之間建立一個完全令人滿意的橋樑。在進行這項工作時，我們不得不使用一種稱為矩(moments)的數學函數。鑑於我們在獲得基態能量方面取得了令人驚訝的成功，我們將論文命名為《神奇的矩》（Magical Moments）。
我清楚地記得我們的一個下午儀式。約翰是一位道地的愛爾蘭人，他總是在四點鐘喝茶；圖1顯示了我們在他家品味茶葉樣本的情景。我們也在 CERN 的餐廳裡進行這個儀式，約翰總是點兩杯他最喜歡的馬鞭草茶，供我們一起享用。我們在那個輕鬆的氛圍下談論物理和哲學。有時，我的藝術家妻子雷娜特也會加入我們，然後我們三人會就現代藝術展開激烈的辯論。
圖1
當約翰·貝爾（右）和我（左）一起工作時，下午茶是必不可少的。這張照片攝於1980年約翰的家。（照片版權所有：雷娜特·貝爾特曼。）
粒子物理學家
約翰是一位備受尊敬的粒子物理學家，他獨特的個性令我著迷。我感受到他父親般的親切，並欽佩他的知識和智慧。他對量子場論有深刻的理解，喜歡用基本的例子來闡述他的想法。他在粒子物理學領域發表了多篇著名的論文，其中我將僅提及其中幾篇。
約翰於1950年代中期提交的博士論文中包含一篇基礎性論文《場論中的時間反演》（Time reversal in field theory）[4]。在這篇論文中，他證明了所謂的CPT定理，其中C是電荷共軛算符，用於將粒子替換為反粒子；P是奇偶性算符，用於通過原點進行反轉；T是時間反演算符。該定理指出，任何滿足一組基本假設的量子場論都必須具有CPT對稱性。（需要說明的是，這些假設包括：理論具有勞倫茲不變性、局部性和厄米特哈密頓量。）多年來，該定理的推導一直歸功於格哈特·呂德斯（Gerhart Lüders）和沃夫岡·包立（Wolfgang Pauli），他們比約翰稍早一些證明了該定理，但如今約翰也得到了應有的認可。
約翰對粒子物理學最深遠的貢獻是一篇題為《PCAC 謎題：σ 模型中的 π0 → γγ》(A PCAC puzzle: π0 → γγ in the σ-model) 的論文，該論文與當時在 CERN 擔任博士後研究員的羅曼·傑基夫（Roman Jackiw）共同撰寫[5]。標題中的「PCAC」代表軸向電流部分守恆（partially conserved axial current）。細節在此不重要，但核心思想是：某種對稱性——即在π0介子質量為零的極限下似乎暗示軸向電流守恆的手性對稱性——排除了π0介子衰變為兩個光子的可能性。謎題的解決方案是：量子化過程本身可能導致古典對稱性的破缺；當這種情況發生時，量子理論被稱為異常理論。說到底，手性對稱異常是π0介子衰變的原因。
史蒂芬·阿德勒（Stephen Adler）在一篇獨立於貝爾和傑基夫的論文中，同樣釐清了異常問題[6]。如今，手性對稱異常通常被稱為阿德勒-貝爾-傑基夫異常。進一步的研究表明，異常不僅是量子化過程的病徵，也是理解量子場論的關鍵 [7]。異常普遍存在於物理理論中，包括粒子物理的標準模型和引力理論。
同樣值得一提的還有約翰與實驗物理學家傑克·斯坦伯格（Jack Steinberger）合著的有影響力的綜述《K介子的弱相互作用》，以及約翰與同事馬丁努斯·韋爾特曼（Martinus Veltman）共同撰寫關於向量玻色子和微中子反應的開創性工作 [8]。
加速器物理學家
1949年，約翰從貝爾法斯特女王大學獲得兩個學士學位後，在哈威爾（Harwell）的英國原子能研究機構開始了他的科學生涯。在那裡，他遇到了未來的妻子瑪麗·羅斯（Mary Ross），她是一名反應堆和加速器物理學家。她當時在理論物理學部門工作，該部門由著名物理學家克勞斯·富克斯（Klaus Fuchs）領導，後者因替蘇聯從事原子間諜活動而被判入獄。1954年，約翰和瑪麗結婚，並開始共同打拚事業。
約翰來到哈威爾不久，他和瑪麗就被派往馬爾文的電信研究機構。在那裡，他們在威廉·沃金蕭（William Walkinshaw）的加速器實驗室工作了約一年。沃金蕭對約翰的能力有相當高的評價，並指出他「是一位才華出眾的年輕人，很快就在研究計畫的選擇上展現了獨立性，特別喜歡粒子動力學。他的數學天賦卓越且優雅。[9]」
約翰發表了多篇論文，有些是與沃金蕭合作，有些是獨自撰寫，主要內容是關於如何在線性加速器中聚焦一束電子或質子。1951年，整個加速器研究實驗室搬回哈威爾；不久之後，約翰轉向粒子物理學研究。到20世紀50年代末，他和瑪麗被歐洲最大的基礎科學實驗室——歐洲核子研究組織（CERN）所吸引。兩人於1960年搬到那裡，約翰加入理論部門，瑪麗加入加速器研究實驗室。
在1980年代，約翰和瑪麗合作進行加速器研究，並共同撰寫了多篇論文。其中一篇是《儲存環中的電子冷卻》，他們分析了電子速度分布的變化如何影響電子在儲存環（如CERN的低能反質子環）中冷卻離子或質子束的能力 [8]。該論文獻給了尤里·奧爾洛夫（Yuri Orlov），他是一位加速器物理學家，因人權活動而在蘇聯入獄，後來獲釋。這種象徵團結的行動是貝爾夫婦的典型做法。
在我看來，貝爾將量子場論中的安魯效應（Unruh effect）與加速器物理學結合的研究尤為引人入勝。根據威廉·安魯的理論，一個在電磁真空中均勻加速的觀察者將觀測到黑體輻射，其溫度與加速度成正比。約翰的想法是使用電子作為加速中的觀察者，並將電子束的偏振用作測量黑體輻射溫度的溫度計。與挪威籍的CERN研究員約恩·萊納斯（Jon Leinaas）共同發表的結果顯示，加速效應雖小但可測量[8]。
我成名了
約翰在CERN是粒子物理的權威人物，許多同事都向他請教，希望得到他的認可。當然，我也聽說他還是量子力學領域的領軍人物——尤其是量子基礎理論方面。但無論是CERN還是其他地方，沒有人能向我解釋他的基礎研究。標準答案是：「他發現了一些數學關係，代表量子力學最終還是正確的。但我們早就知道這一點，所以不用擔心。」我也沒有擔心。至於約翰本人在我們合作初期也從未向我提及他的量子力學研究。
1980 年夏天結束時，我暫時回到我的母校維也納大學。當時還沒有網路，物理學家通常會在論文發表前將預印本寄給全球主要物理學機構。每週，我們在維也納都會將新到的預印本放在一個特殊的架子上展示。
有一天，我坐在電腦室裡整理電腦卡片時，同事格哈德·埃克爾（Gerhard Ecker）衝了進來，手裡揮舞著一份預印本。他大喊：「萊因霍爾德，快看，你出名了！」我難以置信地反覆閱讀約翰論文的標題：「貝特爾曼的襪子與現實的本質」（Bertlmann’s socks and the nature of reality）[8,10]。我完全驚呆了。當我讀到第一頁時，我的心都停了。這篇論文開頭寫道
「路上隨便一個哲學家如果沒有上過量子力學課程，對愛因斯坦-波多爾斯基-羅森［EPR］相關性並不會相當訝異。他可以舉出許多日常生活中類似相關性的例子。伯特爾曼的襪子就是一個常被提及的例子。伯特爾曼博士喜歡穿兩隻不同顏色的襪子。某一天他哪隻腳會穿哪種顏色的襪子完全無法預測。但當你看到第一隻襪子是粉紅色的時，就可以確定第二隻襪子不會是粉紅色的。觀察第一隻襪子，加上關於貝特爾曼這個人的經驗，就能立即得知第二隻襪子的顏色。撇除穿衣品味不談，除此之外，這裡沒有任何神秘之處。而EPR這件事（關於量子相關性）不也是同樣的道理嗎？」
約翰的論文中有一幅漫畫（圖2），描繪了我穿著奇異襪子的樣子；看到這幅漫畫，我差點嚇得跌倒。這太出乎意料了。我完全不知道約翰注意到我穿不同顏色襪子的習慣——這是我從學生時代就養成的習慣，是我參與1960年代抗議的特殊方式。這篇文章立即將我推入了量子辯論，因此真的改變了我的人生。
圖2
我的襪子總是兩隻不同顏色，正如約翰·貝爾在他論文《貝爾特曼的襪子與現實的本質》中附帶的這幅漫畫所提及 [8,10]。 該論文討論了量子與古典相關性的差異，其基礎是法國學院雨果基金會舉辦的一次講座「量子力學的概念含義」。
現在，是時候理解為什麼「EPR問題」不僅僅只是和「貝爾特曼的襪子」同一回事，並欣賞約翰的深刻見解了。我深入研究了他關於隱變量理論和貝爾不等式的開創性著作（見參考文獻8的第3節），以及他關於量子力學基礎的著作 [10]。我對約翰清晰和深刻的思想印象深刻。從此，我們開始就基礎問題展開豐富的討論；這些互動對我來說是一大榮幸。一個新世界向我敞開了——約翰·貝爾的世界——從此，它一直吸引著我。
批判馮·諾伊曼
約翰對量子力學的詮釋從未感到滿意。即使在貝爾法斯特女王大學就讀期間，他就對哥本哈根詮釋中量子世界與古典世界之間的本質區別感到不滿。他好奇量子世界和古典世界之間的界線在哪，並希望消除這種區分。
當大衛·玻姆（David Bohm）發表了他對量子理論的重新詮釋——一種具有隱藏變量的確定性、現實主義理論時 [11]，他的工作並未得到物理學界的認可。例如，愛因斯坦認為它「似乎太廉價了」，而沃夫岡·包立則將它斥為「人造的形上學」。然而，約翰卻深受震撼，並經常感嘆：「我看到不可能的事情被實現了。」 對他而言，很明顯，在對量子理論進行適當的重新架構後，量子粒子的屬性將具有確定性，完全由隱變量支配。「一切事物都有確定性屬性」，他經常這樣說。
隱變量理論對一組可觀測量｛A、B、C、…｝進行建模，並為每個獨立系統分配一組本徵值｛v（A， λ）、v（B， λ）、v（C， λ）、…｝，每個可觀測量對應一個本徵值。請注意，分配的本徵值取決於隱變量（可能不止一個）λ 的值。例如，A、B 和 C 可以是電子自旋的 x、y 和 z 分量，單位為 ℏ/2。那麼，對於特定的 λ 而言，｛v（A）、v（B）、v（C）｝ 可以是 ｛+1、+1、−1｝。狀態集合中的不同成員可以根據各自的 λ 具有不同的正負號分配；因此，隱變量理論還必須為 λ 提供機率分布。當量子狀態（狀態向量加上隱變量的指定）唯一決定測量結果時，該狀態被稱為無色散。
1964 年，約翰開始了他的研究「關於量子力學中的隱變量問題」（On the problem of hidden variables in quantum mechanics）[10]。他在論文中批判了約翰·馮·諾伊曼提出無色散狀態——亦即隱變量——與量子力學不相容的證明。批判的內容是什麼？考慮三個運算符A、B和C，滿足C = A + B。如果A和B可對易，則分配的本徵值必須滿足v（C， λ） = v（A， λ） + v（B， λ）。
然而，馮·諾伊曼將可加性要求同時賦予在不可對易與可對易算符上。貝爾抱怨道：「這是錯誤的。」在給出一般證明之前，他用自旋測量的例子來闡述他的觀點。測量自旋算符σx需要一個特定方向的斯特恩-格拉赫裝置。測量 σy 和 σx + σy 需要不同的測量方向。由於這些算符不能同時測量，因此沒有必要施加可加性。
因此，約翰提出了結果可能取決於儀器設置的模型。此類模型被稱為情境模型，它們可能與量子力學一致。然而，正如著名的科亨-斯佩克定理（Kochen–Specker theorem）所示，所有非情境隱變量理論確實與量子力學互相衝突 [12]。
貝爾定理的創立者
在這篇隱變數論文的結尾，約翰更精確地分析了玻姆對量子理論的重述。他發現根據玻姆的理論，由兩個自旋為 ½ 的粒子（像電子這樣自旋為 ℏ/2 的粒子）所組成的系統中，其中一個粒子的行為會取決於另一個粒子的特性，不論這兩個粒子相距多遠。他思考著：這種相距遙遠的相關性是否只是玻姆隱變數模型獨有的缺陷，還是說這種現象具有更普遍的適用性？於是，他開始著手撰寫他那篇經典的論文〈論愛因斯坦–波多爾斯基–羅森悖論〉，該文包含了一項證明，證明了這種結果具有普遍性——這就是著名的「貝爾不等式」[10]。
約翰所提出的深刻發現是：局域性與量子力學預測的統計結果不相容。他從玻姆版本的 EPR 悖論出發。如圖 3 所示，一對處於自旋單態（即總角動量為零）狀態的自旋 ½ 粒子自由地往相反方向前進，前往兩個稱為 Alice 和 Bob 的測量站。Alice 沿著方向 a 測量自旋（以 ℏ/2 為單位）並得到結果 A；Bob 沿著方向 b 測量並得到結果 B。在隱變數理論中，這些測量結果是預先決定的，並由變數 λ 所指定。
圖 3
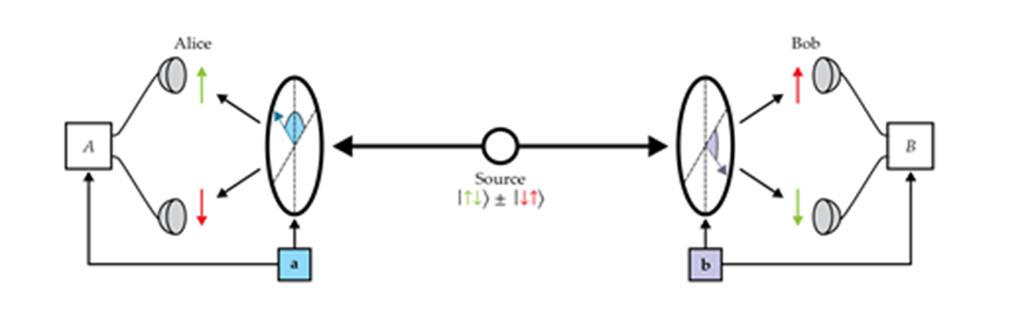約翰・貝爾著名的不等式就是為這種實驗配置所推導出來的。一對自旋為 ½ 的粒子被製備成總角動量為零的狀態，並自由地往相反方向前進，前往 Alice 和 Bob 這兩個測量站。Alice 沿方向 a 測量自旋，而 Bob 同時沿方向 b 測量自旋。在隱變數理論中，測量結果是預先確定的；例如，某個隱變數可能會決定：如果 Alice 測得自旋向上，那麼 Bob 就會測得自旋向下。（改編自 R. A. Bertlmann, J. Phys. A 47, 424007, 2014。）
假設 A 不依賴於 Bob 的測量設定，B 也不依賴於 Alice 的設定——這個假設現在被稱為「貝爾的局域性假設」——那麼 Alice 與 Bob 的聯合自旋測量的期望值可寫為：
$$E(\mathbf{a}, \mathbf{b}) = \int d\lambda \, \rho(\lambda) \, A(\mathbf{a}, \lambda) \cdot B(\mathbf{b}, \lambda).$$
其中函數 $\rho(\lambda)$ 是 $\lambda$ 的標準化分佈函數。 Alice 與 Bob 的測量值必須滿足：$A(\mathbf{a}, \lambda) = \pm 1$， $B(\mathbf{b}, \lambda) = \pm 1$。在這些條件下，約翰得以推導出一個所有符合貝爾局域性假設的隱變數理論都必須滿足的不等式：
$$1 + E(\mathbf{b}, \mathbf{c}) \geq |E(\mathbf{a}, \mathbf{b}) - E(\mathbf{a}, \mathbf{c})|.$$
然而，根據量子力學，E(a, b) = −a · b。因此，如果 a、b 和 c 落在同一平面中，並分別與某一共同軸呈 0°、120° 和 60° 夾角，則量子力學的預測會違反貝爾不等式。
當我第一次推導出貝爾不等式時，我深感震撼：原來我們竟然能夠區分所有隱變數理論與量子力學。約翰究竟是如何找到這個特別的期望值組合，使它在某些測量配置下與量子力學產生衝突的？對我這個理論學家來說，這工作到此已完成。然而，最終還是要靠實驗來決定：究竟是隱變數理論正確，還是量子力學才是對的。
經典實驗
最早開始對貝爾不等式實驗產生興趣的是約翰・克勞澤（John Clauser），他在 1960 年代末開始這項研究。當時從事這個領域的研究需要相當大的勇氣。克勞澤曾提到，他曾經和理查・費曼（Richard Feynman）約好，想討論一個用來檢驗量子力學預測的 EPR 實驗設計。費曼一聽就把他趕出辦公室，說道：「等你真的發現了量子理論在實驗預測上出錯的地方，再回來找我討論吧[13]。」幸運的是，克勞澤並沒有就此放棄，他和史都華・傅里德曼（Stuart Freedman）在 1972 年完成了那次實驗。結果眾所皆知：實驗結果符合量子理論的預測，並明顯違反了貝爾不等式。後來，愛德華・弗萊（Edward Fry）和藍道・湯普森（Randall Thompson）也進行了類似的實驗並確認了這項結果 [14]。
到了 1980 年代，第二代貝爾實驗展開，特別是阿蘭・阿斯佩（Alain Aspect）及其研究團隊的工作 [15]。阿斯佩等人使用偏振光子，並引入快速切換偏振片的機制，以排除 Alice 和 Bob 之間可能的互相影響。結果再次明確違反了貝爾不等式，且實驗結果與量子力學的預測相符。在我看來，阿斯佩的實驗是個轉捩點；物理學界開始意識到這些實驗是在指向某些極為根本的事物。也因此，研究開始轉向今天所謂的「量子資訊」和「量子通訊」——一個蓬勃發展的領域。
第三代貝爾實驗始於 1990 年代，並延續至 21 世紀。這一代實驗充分利用了新技術，例如自發參數下轉換（spontaneous parametric down-conversion），這是產生糾纏光子的有效方式。安東・蔡林格（Anton Zeilinger）與其團隊完成了一項劃時代的實驗，確保測量光子偏振方向的設定是隨機且彼此獨立的 [16]。隨後出現了一系列令人著迷的實驗，包括量子傳送、量子密碼學，以及遠距離量子通訊等。
偉大的謎團
所有貝爾不等式的核心要素就是貝爾的「局域性假設」。到目前為止，所有試圖檢驗貝爾不等式的實驗都觀察到了違反的情況，因此我們不得不與約翰得出一樣的結論：自然界的結構中包含了非局域性。這樣的非局域性讓約翰非常困擾，因為對他來說，這等同於破壞了勞倫茲不變性——這是一件他難以接受的事。他常說：「這對我來說是一個巨大的謎團。幕後似乎有某些東西比光速還快。」
約翰完全相信「實在論」（realism）是作為科學家的正確立場。也就是說，他相信實驗結果是在測量之前就已經被預定好，而不是由測量行為所產生。在他對 EPR 糾纏關聯的分析中，他並不是假設「實在性」，而是從推理中得出這個結論。他曾說過：「這很神秘，就好像你看了一隻襪子，這隻襪子就變成粉紅色，而另一隻襪子同時變成不是粉紅色。」即使 EPR–貝爾實驗的結果與他期望的隱變數理論不符，他仍然堅持這條研究路線，並未因此灰心，反而覺得這些結果令人困惑。他曾對我說：「這個狀況非常耐人尋味——在所有為人稱道的成功（量子力學）背後，居然潛藏著如此深刻的疑問。」
在他那篇〈伯特曼的襪子〉論文的結尾，約翰再次表達了他的擔憂：
「也許我們真的得承認：因果關聯確實能以超光速傳播。在完整的理論中，勞倫茲不變性的角色將變得非常棘手。某種『以太』可能是最便宜的解法。但這種以太若無法被觀測到，將令人困擾；而若不能用它傳送比光速還快的訊息，那也同樣令人不安。」
為了回敬約翰那篇〈伯特曼的襪子〉，我在 1988 年他的 60 歲生日時發表了一篇題為〈貝爾定理與現實的本質〉（Bell’s Theorem and the Nature of Reality）的論文獻給他 [17]。我在文末畫了一幅漫畫（見圖 4），表達我的結論。約翰是一個完全滴酒不沾的人，但他被這幅漫畫逗樂了，因為裡面那個「詭異的非局域幽靈」是從一瓶貝爾牌威士忌中冒出來的——這牌子真的存在。
圖 4
這幅漫畫中同時存在真實的威士忌瓶與詭異的幽靈，作為獻給約翰・貝爾 60 歲生日的論文結語 [17]。
當我回顧與約翰的合作，想起他誠懇的個性與溫暖的友誼、深刻而銳利的智慧，以及我從他那裡學到的知識。能與他共度那些時光，我感到無比的榮幸與感恩。那的確是些充滿魔力的時刻（magical moments）。
我要感謝芮娜特・貝特爾曼（Renate Bertlmann）多年來的陪伴，以及她提供的圖1。
參考文獻
1. J. S. Bell, R. A. Bertlmann, Z. Phys. C 4, 11 (1980). https://doi.org/10.1007/BF01477302
2. J. S. Bell, R. A. Bertlmann, Nucl. Phys. B 177, 218 (1981); https://doi.org/10.1016/0550-3213(81)90389-8Phys. Lett. B 137, 107 (1984); https://doi.org/10.1016/0370-2693(84)91115-8
Phys. Lett. B 137, 107 (1984); https://doi.org/10.1016/0370-2693(84)91115-8
R. A. Bertlmann, Nucl. Phys. B 204, 387 (1982). https://doi.org/10.1016/0550-3213(82)90197-3
3. J. S. Bell, R. A. Bertlmann, Nucl. Phys. B 187, 285 (1981); https://doi.org/10.1016/0550-3213(81)90274-1
R. A. Bertlmann, J. S. Bell, Nucl. Phys. B 227, 435 (1983). https://doi.org/10.1016/0550-3213(83)90567-9
4. J. S. Bell, Proc. R. Soc. London A 231, 479 (1955). https://doi.org/10.1098/rspa.1955.0189
5. J. S. Bell, R. Jackiw, Nuovo Cimento A 60, 47 (1969). https://doi.org/10.1007/BF02823296
6. S. L. Adler, Phys. Rev. 177, 2426 (1969). https://doi.org/10.1103/PhysRev.177.2426
7. R. A. Bertlmann, Anomalies in Quantum Field Theory, Oxford U. Press (2000). https://doi.org/10.1093/acprof:oso/9780198507628.001.0001
8. M. Bell, K. Gottfried, M. Veltman, eds., Quantum Mechanics, High Energy Physics and Accelerators: Selected Papers of John S. Bell, World Scientific (1995).
9. P. G. Burke, I. C. Percival, Biogr. Mem. Fellows R. Soc. 45, 1 (1999). https://doi.org/10.1098/rsbm.1999.0001
10. J. S. Bell, Speakable and Unspeakable in Quantum Mechanics, 2nd ed., Cambridge U. Press (2004).
11. D. Bohm, Phys. Rev. 85, 166 (1952); https://doi.org/10.1103/PhysRev.85.166
D. Bohm, Phys. Rev. 85, 180 (1952). https://doi.org/10.1103/PhysRev.85.180
12. See, for example, J. Conway, S. Kochen, in Quantum [Un]speakables: From Bell to Quantum Information, R. A. Bertlmann, A. Zeilinger, eds., Springer (2002), chap. 18.
13. J. F. Clauser, in ref. 12, p. 71.
14. E. S. Fry, in ref. 12, chap. 8.
15. A. Aspect, in ref. 12, chap. 9.
16. G. Weihs, in ref. 12, chap. 10.
17. R. A. Bertlmann, Found. Phys. 20, 1191 (1990). https://doi.org/10.1007/BF01889465
本文感謝Physics Today (American Institute of Physics) 同意物理雙月刊進行中文翻譯並授權刊登。原文刊登並收錄於Physics Today, Jan. 2025雜誌內 (DOI: 10.1063/pt.peha.bftv )。原文作者：Reinhold A. Bertlmann。中文編譯：林祉均。
Physics Bimonthly (The Physics Society of Taiwan) appreciates Physics Today (American Institute of Physics) authorizing Physics Bimonthly to translate and reprint in Mandarin. The article is contributed by Jaco de Swart and was published in (Physics Today, Jan. 2025;DOI: 10.1063/pt.peha.bftv ).The article in Mandarin is translated and edited by J.R Lin.
