
在日常使用者與他們所操作的精密、易錯的硬體之間,隔了很多夾層。
大多數人坐在電腦前面工作時,想的都是需要完成的事,鮮少會去考慮他們的按鍵及滑鼠點擊是如何轉換成邏輯操作及電訊號。硬體與使用者介面之間的分隔,是好幾十年發展的結果,現在,量子電腦開發人員正開展類似的探索。
量子計算堆疊(quantum computing stack)描述介於使用者與物理量子位元(physical qubits)之間的一切,它需要執行必要的功能,例如,讓使用者介面更方便、將輸入轉換成硬體操作、以及修正多個錯誤來源(關於量子結構的更多資訊,請參閱Anne Matsuura, Sonika Johri與Justin Hogaboam於Physics Today的文章,2019年三月號第40頁。) 然而,還沒有一種正確的方法能將這些任務劃分成離散的層級,所以研究人員和科技公司仍在追求未來量子架構的不同願景。
在Physics Today 的2021年三月號第28頁的文章當中,Harrison Ball、Michael Biercuk 與 Michael Hush介紹了Biercuk所創立的量子科技公司Q-CTRL提出的量子計算堆疊概念,作者們詳細解釋量子韌體層(quantum firmware layer,量子電腦的組成部分之一)的功能對管理量子位元的誤差的重要性,本文中我們將解釋量子電腦其它各層所發生的事情。
量子位元硬體
古典電腦以0或1的位元儲存資訊,這些位元的底層是作為開關的場效電晶體,值可為0或1,取決於其開或關的狀態。在最基本的層級,電腦所做的每件事――儲存資訊、執行計算、跑程式――都只是利用小小的電壓來操控這數十億個位元的值。
而量子電腦則是仰賴量子位元,它可處在 $|0\rangle$ 或 $|1\rangle$ 其中一個量子態,或這兩個態的線性疊加 $|\psi\rangle = \alpha|0\rangle + \beta|1\rangle$,其中係數 $\alpha$ 跟 $\beta$ 與發現量子位元處於各別量子態的機率有關。
為什麼量子位元存在疊加態很有用呢?這要比較在n個獨立位元與相同數目透過糾纏(一種無法以古典物理描述的現象)連結的量子位元可儲存的資訊多寡。
每一個古典位元僅需要一個值來描述它是開或關的狀態,因此 $n$ 個位元代表 $n$ 個二進位元 (binary digits),乍看之下,量子位元似乎有 $2n$ 個數,類似那些二進位元,因為每一個量子位元都有兩個係數 $\alpha$ 和 $\beta$,但量子位元的優勢可比這還大:描述一個由 $n$ 量子位元組成的量子態需要高達 $2^n$ 個係數!
例如,考慮一個三量子位元系統,每個量子位元可處在 $|0\rangle$ 或 $|1\rangle$ 的量子態,因此系統可被測到在八種可能狀態――而八個係數描述每個態的機率。系統的量子位元數越多,勝過古典位元的資訊優勢就越大,然而,要利用這龐大的計算空間絕非易事:編寫受益於量子位元特性的演算法是個挑戰,因為儘管計算操作了 $2^n$ 個係數,但它們僅輸出 $n$ 個值――量子位元的終態 (欲了解更多資訊,請參閱下方有關量子演算法的部分) 。
雖然古典計算大多選定在一種類型的位元硬體,量子位元仍然有許多種類。任何二能階量子系統(列舉一小部分如原子核自旋、光子偏振、或量子點自旋等)都可用來作為量子位元,不過,一個特定系統的實用性決定於幾個因素,像是量子位元是否容易操控與糾纏、它們維持在所需量子態的時間長短,以及它們的狀態是否容易被外界雜訊給摧毀。
一個常見實現量子位元硬體的例子是離子阱量子位元(trapped-ion qubits),在此設計裡,帶電粒子被電磁阱困住,價電子於兩個量子態間移動做為量子位元。中性原子中的超精細躍遷 (參閱David Weiss 與 Mark Saffman於Physics Today的文章,2017年七月號第44頁),以及量子點中的電子自旋翻轉(參閱Lieven Vandersypen 與 Mark Eriksson於 Physics Today的文章, 2019年八月號第38頁)都有相同功能。
而一些最著名的量子電腦,包含 IBM 和 Google 研發的,都是仰賴 transmon 超導量子位元,transmon 是電荷的超導島 (superconducting islands),其中 $|0\rangle$ 與 $|1\rangle$ 之間的差別在於是否存在一個額外的束縛電子庫柏對 (Cooper pair)。
量子韌體

冷凍系統內裝有一台IBM Q System One量子電腦(圖片來自IBM)。
量子位元非常容易出錯,各種環境因素如熱擾動、電磁輻射、磁場等,都能讓量子位元喪失它的預期狀態,這種資訊的流失稱為去同調或去相干 (decoherence),可在瞬間發生。儘管利用冷卻可以減少熱擾動,但去同調最終還是會不知不覺地出現,並且產生硬體錯誤,像是意外將量子位元從 $|0\rangle$ 翻轉到 $|1\rangle$ 量子態 (常用的冷卻系統,如上圖所示的 IMB 冷卻系統 , 就是許多人在想像一台量子電腦時所構思的)。一個量子位元能執行的操作次數受到去同調時間的限制,除此之外,每一組量子位元硬體都有其獨特的理想性能偏差。(參閱 Ian Walmsley 與 Herschel Rabitz 於 Physics Today 的文章,2003 年八月號第 43 頁)
不過高階的量子計算堆疊不能被期待去處理這類系統之間的差異,程式設計師需要能在不知底層硬體的特性下,去請求執行一個操作。(想像假如每一台電腦都需要個人化的軟體!)
量子韌體為高階的計算堆疊創造一個量子位元硬體的虛擬版本,它專注在所有能用來穩定硬體及緩和誤差的低階量子控制任務,例如,它利用硬體的資訊來自主定義射頻(RF)或微波脈衝的抗錯版本,作用於量子位元以執行量子邏輯運算。

黃金電極在離子阱量子電腦中產生帶電粒子的阱。此電極的構造允許微波與雷射光束進入,而整個系統裝置於一個超高真空的真空腔內 (照片提供:雪梨大學Michael J. Biercuk)。
雖然單靠量子韌體不能解決硬體錯誤的問題,但它對抑制硬體參數(如量子位元共振頻率)的緩慢漂移―這是量子計算硬體的骯髒秘密―特別有效,這能力使得量子韌體成為適合處理隨機錯誤的量子糾錯協定(error correction protocols)的強力搭配。
更多關於量子韌體層的資訊,請參閱稍早提到Ball、Biercuk與 Hush在Physics Today的文章。
硬體感知量子編譯器
在古典電腦中,編譯器(compiler)接收需完成任務的高階指令,將這些指令轉換成一系列操作交由底層硬體執行。同樣的事也發生在量子電腦內。
「硬體感知量子編譯器(hardware-aware quantum compiler)」也稱為轉譯器(transpiler),負責從考慮量子位元之間物理連接的方式,找出完成一組邏輯運算的方法。雖然物理量子位元不能輕易移動,但兩個量子位元的態可以互換做有效的重新排列,轉譯器會根據硬體的約束條件(像是哪些量子位元彼此直接連接),找到如何去實現量子位元之間的任意運算,它還可以決定每次運算使用哪些量子位元——例如,假使已知特定量子位元有問題,資訊就可能就需要繞過它。
在現階段的量子計算時代裡,硬體感知編譯器是唯一的編譯器,也因如此,它背負著減少執行演算法所需的量子邏輯運算次數的額外責任,用此來最佳化量子位元的使用能讓任務盡可能地快速完成,這很重要,因為量子位元態的壽命非常短。
量子糾錯
即使有了量子韌體,錯誤還是不可避免地從去同調與不完美的量子位元操控中產生,量子糾錯(QEC)的設計是用來偵測並修正這些錯誤,它透過把資訊散播在許多量子位元來防止單個量子位元出錯。每個糾錯物理量子位元組構成了一個邏輯量子位元,接著可使用於量子電路。令人驚訝地,邏輯量子位元經過設計可以讓底層量子位元態就算發生去同調,邏輯量子位元的態依然存在,原則上無限。
一旦將邏輯量子位元進行編碼,就會使用複雜的演算法來辨別錯誤,並以不失編碼資訊的方式進行修正(直接對量子位元進行測量會破壞它們的量子態),一個簡單的執行是利用冗餘(redundancy)來提供保護:即使其中一個量子位元最後處在錯誤的態,它們全部出錯的機率也會降低。
使用QEC修正量子位元錯誤―在本質上是相當耗費資源的―一些目前的配置中,每個邏輯區塊使用高達數十個物理量子位元――而且可能需要比現有設備更多的量子位元來提供任何實質效益。因此,QEC從長遠來看比現在的機器更為重要,量子韌體的目的在於處理更多可預測的雜訊來減低QEC程序的負擔,進而提高QEC的資源效率。
邏輯層級的編譯與電路最佳化
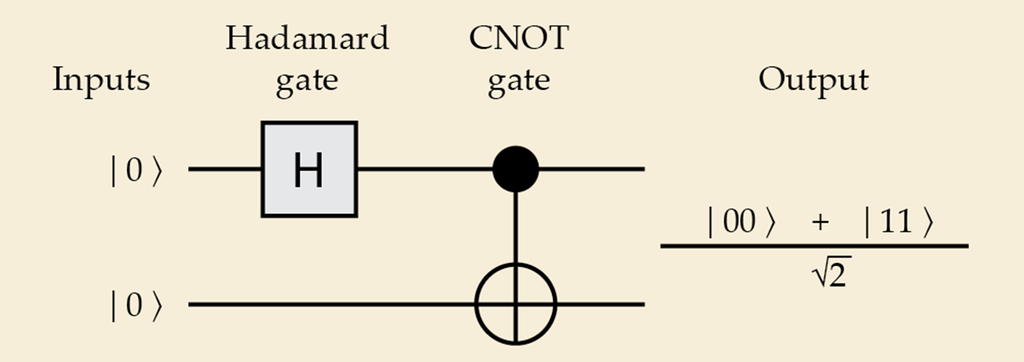
兩個量子位元初始於純的 $|0\rangle$ 態,Hadamard 閘作用於第一個量子位元,並將它置於 $|0\rangle$ 與 $|1\rangle$ 的疊加態,量子位元在每一個態的發現機率相等。只有在控制量子位元 ($\bullet$) 處於 $|1\rangle$ 態時,雙量子位元 CNOT 閘將目標量子位元 ($\oplus$) 翻轉為 $|1\rangle$,因而產生如圖示的糾纏輸出態 。貝爾態被應用在例如:量子密碼學。(參見 Marcos Curty、Koji Azuma 和 Hoi-Kwong Lo 的文章,Physics Today 2021 年三月號第 36 頁)
量子電路是指一組序列的邏輯閘,作用於一系列的量子位元來執行某個演算法。上圖為一個簡單的電路範例,將兩個Bell態的量子位元糾纏。
左邊為初始量子位元態,右邊為終態,兩者之間為一連串的邏輯閘,指示各個量子位元上執行的運算。電路中表示的量子位元並不是物理量子位元,而是稱為邏輯量子位元的抽象物件,一個邏輯量子位元可利用多個互相作用的物理量子位元來實現,它們的硬體錯誤由QEC緩解。
單一演算法可表示成多個邏輯等效的電路,而電路最佳化的目的在於找出需求最少運算或時間步數的電路,執行愈少的運算可使演算法跑得愈快,這在任何量子電腦中不管是否使用QEC都是重要的目標。
當未來量子糾錯(quantum error correction,QEC)能被經常性使用時,這責任的一部分將由高階邏輯層編譯來承擔,而低階編譯器的任務會是將邏輯量子位元運算轉換成其組成物理量子位元的操控。
量子演算法與應用
量子演算法與古典演算法的作用相同,都是一步一步提供指示來完成一個計算任務。
雖然一般演算法原則上可在量子電腦上執行,但真正的量子演算法應用了底層硬體的量子特性。舉例來說,在量子電腦中操控一個量子位元,會影響整個n量子位元態還有描述它的所有2n個係數,有效地同時處理許多運算。不過,這不太算是平行計算,最終的量子位元態在測量時,每個不是0就是1,演算法的輸出只有n個值,而不是所有2n個係數。(更多關於量子計算的資訊,可參考如Charles Bennett的文章,Physics Today 1995年十月號第24頁)
鑒於測量上的限制,要真正能利用量子電腦的龐大計算空間相當困難,整個量子演算法開發的領域,就在致力於找出能夠有效使用資源的方法。一些問題像是質因數分解,已知可以透過量子演算法加速,這個加速反映在演算法得到答案所必須經過的步數:傳統電腦做質數因式分解所需的步數隨著數字大小呈現指數性成長;而對於量子電腦僅是呈多項式成長。量子傅立葉轉換也是比它們的古典對應明顯快許多。不過其它的任務,像是下西洋棋,幾乎無法從量子演算法獲得利益,因為隨著問題的複雜性增加,所需的步數仍舊增加太快。
變分量子演算法(variational quantum algorithm)是古典與量子演算法之間的折衷,它將計算分解為一個小的量子部分和一個大的古典最佳化問題,因此,需要的量子電腦比量子傅立葉轉換小許多,這種演算法有希望能解決金融、物流與化學方面的問題。
使用者介面、QAAS與操作系統
大部分想要使用量子電腦的人不會建造或甚至去購買一台量子電腦――至少在短期內不會,為了促進有限的現有量子計算資源的存取,大公司匯集雲端基礎設施允許遠端操作。和古典電腦一樣,量子計算堆疊的最高層級提供與使用者互動的介面。
Amazon Braket、Microsoft Azure Quantum 和 Rigetti Quantum Cloud Services都是給予「量子即服務」(quantum-as-a-service,QAAS)的例子,不過,這些大公司並不一定會提供他們自己的量子電腦作存取,而是連結使用者與電腦,例如,Amazon Braket可讓用戶連接到D-Wave、 Rigetti 與 IonQ的資源。這個方法讓量子電腦類似於其它管理的雲端計算資源,像是圖形處理器(graphical processing units)。
上列的服務可使用高階程式語言來撰寫程式碼,得到的演算法對於有程式經驗的人來說,也許看起來並不奇特。譬如,開源軟體開發工具Ocean (D-Wave)、Qiskit (IBM)與Forest ( Rigetti)支持Python程式語言,而專用於量子計算的語言包括了Quantum Computation Language (QCL,類似C語言)及Q語言(作為C++的延伸)。程式碼定義一系列操作,這些操作組成了一個邏輯演算法。
 這簡短的 $\text{Qiskit}$ 演算法類似「Hello, World!」程式,將一個量子位元初始化為 $|1\rangle$ 態 (圖片來自 D. Koch, L. Wessing, P. M. Alsing, http://arxiv.org/abs/1903.04359)。
這簡短的 $\text{Qiskit}$ 演算法類似「Hello, World!」程式,將一個量子位元初始化為 $|1\rangle$ 態 (圖片來自 D. Koch, L. Wessing, P. M. Alsing, http://arxiv.org/abs/1903.04359)。
本文感謝Physics Today (American Institute of Physics) 同意物理雙月刊進行中文翻譯並授權刊登。原文刊登並收錄於Physics Today, Mar. 2021雜誌內 ( DOI: 10.1063/PT.6.1.20210305a )。原文採訪: David Zierler 改編/註譯:Ryan Dahn。中文編譯:張鳳吟,國立陽明交通大學物理學系博士。
Physics Bimonthly (The Physics Society of Taiwan) appreciates Physics Today (American Institute of Physics) authorizing Physics Bimonthly to translate and reprint in Mandarin. The article is contributed by Francis Duck and was published in (Physics Today, Mar. 2021; DOI: 10.1063/PT.6.1.20210305a ). The article in Mandarin is translated and edited by F. Y, Chang, National Yang Ming Chiao Tung University.

