
聯合國宣布2025年為國際量子科學技術年,主要的原因當然是百年前年輕的德國科學家海森堡提出了第一個版本的量子力學,今天稱之為「矩陣力學」。關於其中的來龍去脈,筆者已經在前文介紹過了。
但是1925年的重要性並不單單只是矩陣力學的出現而已。如果仔細考察爬梳,還可以發現另有兩項重要的物理觀念,就在這一年從伏流變成噴泉,幾年之後甚至變成汪洋一片:那就是「包立不相容原理」與「物質波」。這兩個觀念對量子物理的發展,其實有非常深遠的影響,尤其是對後續的量子場論的成形,更是至關重要,更有意思的是,這兩個概念其實彼此激盪,互為表裡,但是一般回溯量子物理的文章,似乎絕少著墨於此。所以筆者希望趁這個百年一遇的機會,把這段歷史交代清楚,讓各位讀者能對量子物理發展的來龍去脈能夠有更宏觀的掌握。
首先讓我們先從包立的「不相容原理」談起。包立在1925年1月16日提交發表的論文《電子的封閉殼層的分類與光譜的複雜結構》中,詳細闡述了這個原理如下:
「一個原子中任何兩顆電子不可能四個量子數都相同。如果一個電子存在於一個原子中,並且這些量子數都有確定的值,那麼這個狀態就是‘被佔據’的。」
這就是赫赫有名的包立不相容原則。但是這個原理是怎麼出現的呢? 這可要話說從頭了。早在1922年,包立與波爾在哥廷根第一次見面時,波爾就曾向包立表示:「為何電子不會都擠在最內層,而會有造成化學活性的外層電子,是一件難以解釋的大問題!」這是因為物理系統應該會自動趨向最低能量的狀態。所以波爾有此一問。但是波爾的為學方式十分神奇,他常常能夠在未知的混沌中變出鮮豔的花朵來。所以他放手去研究原子模型與化學週期表的關聯。波爾首先是從惰性氣體的原子序看出端倪。他推測最內一層(K-shell)的電子數最多到2,第二層(L-shell)則是8。他更進一步主張L-shell的8個電子應該是分成4+4。
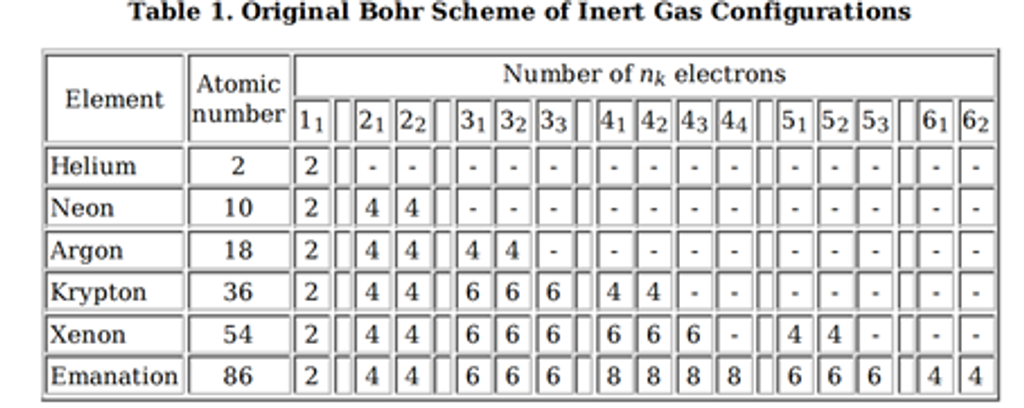
但是這個顯然到了氪就行不通了,由上表發現,要解釋氪氙氡,高層的電子數會改變! 所以答案顯然沒那麼簡單。三年之後,包立終於能夠解釋惰性氣體的電子數,但是這過程可真是百轉千折,就讓我們跟著包立的腳步,亦步亦趨,看他是如何解開這個謎團。
包立的出發點,並非週期表,而是鹼金族金屬如鈉的季曼效應。雖然季曼在1896年發現了元素光譜在磁場下會分裂的現象,而羅倫茲在得知這個結果後很快就利用古典電動力學就加以解釋,兩人還因此得到1902年的諾貝爾物理獎,
羅倫茲的理論是假設電子的圓周運動時,隨著不同的磁場方向,圓周運動的半徑會變大或是縮小,回轉頻率也跟著變小或變大,把電子迴轉頻率的改變等同於光譜線頻率的改變。但是其實光譜線的頻率與光譜線的頻率其實並不相同。
其實季曼效應是一個不折不扣的量子效應,在索末菲改良過的原子模型下得到了相應的解釋,原子能階會照著能階的磁量子數分裂,而磁量子數的數目與它的角量子數L有關,依照索末菲的計算,磁量子數應該從 -L到 L,一共是2L+1個。但是鈉的光譜中,有名的D1與D2 兩條光譜線在磁場下分裂成四道與六道光譜線,這代表L是半整數! 這個現象被稱為是異常季曼效應。
包立的師兄,索末菲的學生,阿弗烈德·蘭德是當時所有研究異常季曼效應最有成就的物理學家。他假設原子核與內層電子會組合出一個角動量,他稱之為”核”角動量,蘭德假設”核”角動量與電子的軌道角動量耦合,他讓電子軌道角動量與它產生的磁矩的比例常數(稱之為g 因子)與核”角動量與它產生的磁矩的比例常數不同,前者設定為1,後者為2,由此推導出著名的蘭德g因子公式。然而更進一步要用蘭德的模型來解釋電子因原子內部固有磁場所產生的精細結構時,卻失敗了。事實上D1與D2 兩條光譜線在索末菲模型中對應的量子數躍遷是相同的,蘭德模型連D1與D2 的能量差也無法解釋。而包立當時就是想要試圖解決這個問題。但是就算是包立也發現自己身陷窮地......。
包立最後的答案令人吃驚。他在1923年四月寄出第一篇關於異常季曼效應的文章《 關於異常季曼效應的規律Uber die Gesetzm¨assigkeiten des anomalen Zeemaneffektes》,包立強烈認為強磁場下的帕申-巴克效應是解開問題的關鍵。在強磁場下,電子的軌道角動量還來不及與「神秘」的角動量耦合,它們個別與磁場作用讓能階分裂,經過分析,包立認定這個「神秘」的角動量擁有雙值,要嘛+1/2, 要嘛-1/2,而且這個未知量子數,是電子內秉的性質,而且還是個完全非古典的自由度。
他在論文最後寫下這段話:
我們未能對所提出的規律,尤其是本段討論的形式規則,提供令人滿意,基於模型的解釋。正如引言中已經提到的,基於迄今為止已知的量子理論原理,這種解釋幾乎是不可能的。一方面,拉莫爾定理的失效表明,原子的角動量和磁矩之間的關係並不像古典理論要求的那麼簡單,因為必須放棄畢歐-沙伐定律,或者修改角動量的力學概念。另一方面,m和j的半整數值的出現已經代表了與多週期系統量子理論架構的根本性突破。
在量子物理發展的過程中,這應該是頭一遭有人懷疑在原子尺度下,古典力學是否依然適用。雖然早在十年前波爾就對電動力學是否能在原子尺度下是否適用提出懷疑,並且主張電子在特定軌道不發出輻射,但是他可從沒懷疑過古典力學的適用性。這麼重大的進展伴隨的不是狂喜,而是眼淚!包立在寫給索末菲的信中說:
我對異常季曼效應苦思了很久,經常誤入歧途,測試又否定了無數假設。但就是說不通!我只是又徹底搞錯了一次!有一段時間,我徹底絕望了……我含著淚水寫下了整篇文章,完全沒有享受到其中的樂趣。
包立接著在1923年7月寫給索末菲的信中寫道:
這(異常既曼效應)似乎指向某種非力學的東西。
他還寫信給蘭德:
我確信,在異常季曼效應中,不存在多周期模型,必須做一些本質上新的事情。
在百般不情願的情況下,包立在 1924 年 12 月送出下一篇論文。他首先利用索末菲的舊量子論計算蘭德模型的磁矩與角動量比的相對論效應,結果與實驗完全不搭,由此他確定蘭德模型不可能是正確的方向,他開始相信異常季曼效應裡出現的未知角動量應該就是來自電子自身。接著他專注於鹼金族的異常季曼效應。包立使用四個量子數來表徵鹼金族原子中電子的狀態:$n$、$l$、$j = l \pm 1/2$ 和 $m_j$(以現代符號表示);他以 $n$ 和 $l$ 表示當時眾所周知的主量子數和角動量量子數,以 $j$ 和 $m_j$ 分別表示總角動量及其空間投影。用這樣的量子數解釋完鹼金族光譜後,包立突然話鋒一轉,寫道:
根據這個觀點,鹼金族光譜的二重態結構以及與拉莫爾定理的偏差,是由於電子的量子理論性質具有特殊的雙值性,而這無法從古典物理的角度來描述。
包立自始至終強調這個雙值性是非古典是有根據的,正如其他幾位年輕物理學家後來主張這個新角動量是來自電子自轉,包立顯然也想過這個可能性,但是他很快就發現如此一來電子自轉速度將會超過光速,此外他也注意到,如果設定這個「新角動量」對應的磁矩之間的g值為2時,它與原子內部磁場的耦合產生鹼金屬光譜的超精細結構會是實驗值的兩倍!這個問題一直困擾著他。
但是就在包立發表第二篇論文前,另一項發現讓包立大為振奮。1924 年 7 月,年輕的英國物理學家埃德蒙·斯托納 (Edmund Stoner) 提出了原子中決定化學性質的電子殼層的數目應該是 $2(2k-1)$,在這裡,$k=l-1$,其中 $k=1, 2, 3, \dots, n$。$k=1$ 對應到的殼層電子數是 $2$,$k=2$ 對應到殼層電子數是 $6$,所以 $\text{L-shell}$ 的 $8$ 顆電子應該分成 $2+6$,而不是波爾主張的 $4+4$。斯托納 (Edmund Stoner) 的主張雖然與波爾先前主張的數值有所不同,但卻與 $\text{X}$ 射線吸收的實驗結果一致。這個選擇也給出了正確的化學週期長度 $2n^2$,因為
$$\sum_{k=1}^{n} 2(2k-1) = 2n^2.$$
更有趣的是,斯托納指出,改用 $l=k+1$,數字 $2(2l +1)$ 表示給定 $n$ 和 $l$ 的鹼金屬元素 ($l < n$) 的季曼分量的數量:
l =0,2個能階
l =1,6個能階
l =2,10個能階
依照索末菲模型,給定 n 和 l 的鹼金屬元素( l < n)的季曼分量的數量是2l+1,多出來的這個因子2 正是這個所謂「神秘,非古典」的新自由度呢!
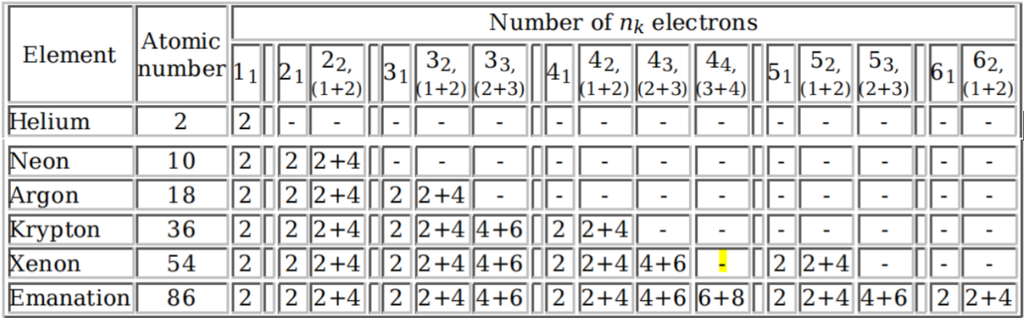
所有的線索都指向同一個方向,所以包立在1925年1月16日發表了論文《電子的封閉殼層的分類與光譜的複雜結構》,提出了我們今天所稱的包立不相容原則。依照這個原理,原子中的每個電子都有一組獨特的量子數(主量子數,角量子數,磁量子數還有不知名的第四個量子數)。而且在原子中的電子都必須擁有不同的量子數。如果這個原理不成立,原子中的所有電子都會堆積在最低能態,那麼不僅周期表不會成立,而且自然界中的原子也不可能形成化學鍵,我們的物質世界也會崩潰!所以包立提出來的這個原則真是太重要了。但是向來毒舌的包立這一次卻成了師弟海森堡毒舌的受害者了,因為當海森堡讀了這篇論文之後,他的回信可樂著了:
「今天我讀了你的新作品,毫無疑問,我是其中最高興的人,不僅因為你引入具有 4 個自由度的單個電子,把騙局推向了難以想像的、令人眩暈的高度,從而打破了迄今為止你侮辱我的所有記錄。」
一來是海森堡當年在處理氦原子光譜時企圖引入半整數量子數曾經被包立毫不留情地口筆撻伐,結果居然自己也引入半整數量子數,再者包立不相容原理似乎暗示原子內的電子能察覺周遭的電子的量子數,否則如何能夠保證每個電子都能擁有不同的量子數,但是這些電子都是點狀粒子,而且都在各自的軌道上運動,怎麼能夠跟鄰近的電子打 PASS?這簡直是太匪夷所思了吧?
不! 這不但不匪夷所思,而且還是量子物理的一大基柱「全同性」這個概念的濫觴。另一個在1925年破繭而出的概念,也與此緊密相關,這個概念就是隔年出現的波動力學奠基於上的「物質波」概念,或者更精準地說,是一般物質的波粒二象性。這個概念影響物理發展的過程也是相當曲折,雖然在1923年法國的年博士生路易·德·布羅伊親王就寫在他的博士論文上,但是這個概念真正得到物理界的重視,卻得從1924年夏天愛因斯坦在柏林收到的一封信講起。1924年的夏天,愛因斯坦收到一封來自英屬印度達卡的信,這封信是從英國印度達卡大學的講師薩特延德拉·納特·玻色(Satyendra Nath Bose)寄來的。玻色是愛因斯坦的鐵粉,他尤其對愛因斯坦的光量子理論感興趣。在20世紀20年代初玻色想要嚴謹地推導出普朗克的輻射公式。 他使用愛因斯坦的光量子的概念,企圖建立質量為零的粒子的統計模式,並由此導出輻射公式。雖然早在1900年普朗克就提出了黑體輻射公式,但是他的推導是假設電磁波與物質交換能量的量子化而得,後來愛因斯坦提出了AB係數以此來推導黑體輻射,可是他們還是用了許多古典物理的對應,玻色認為光憑愛因斯坦的光量子理論就應該足以推出正確的黑體輻射公式,因為它本質上就是光子氣體的統計分布。據說他原本要在課堂上示範,把黑體輻射當作光子氣體的話會得到高頻的維恩分布,但是陰錯陽差,他居然在課堂中得到普朗克分布,由此領悟出一個新的統計法則,由此可以推導出普朗克的輻射強度分布。 他將這個想法寫成論文,但是屢次被退稿, 因為歐洲的期刊的編輯們顯然無法理解這篇論文。 玻色只好把他的論文寄給了愛因斯坦,他不只希望愛因斯坦能幫他翻譯成德文,還希望能幫他把文章發表在期刊上。到底玻色發現的神奇新統計原則是什麼呢?
在古典力學中,系統中的所有粒子都被認為是可區分的。 這意味著可以標記和跟踪系統中的每個粒子。 因此,改變系統中任何兩個顆粒的位置導致整個系統的完全不同的配置。 古典統計稱為馬克士威 - 波茲曼統計。 將其與古典力學區別開來的量子力學的基本特徵是特定類型的粒子彼此是不可區分的! 這意味著在由類似粒子組成的組合中,交換任何兩個粒子不會導致系統的新配置。 愛因斯坦很快就看出它的價值,所以不但把玻色的論文翻成德文,還幫助他的論文被發表在期刊上。這就是玻色-愛因斯坦統計(Bose-Einstein statistics)。這是第一個量子統計規則,當然,一開始,玻色也好,愛因斯坦也好,對於這個統計規則適用於哪些對象,可是一點頭緒也沒有。不過薑還是老的辣,愛因斯坦當年曾將普朗克的量子假設拿來處理晶格振動,一舉解決晶體低溫比熱的難題,所以愛因斯坦故技重施,大膽地將玻色的統計拿來用在單原子理想氣體上,他把光量子的能量-動量的關係換成一般擁有靜止質量的物質能量-動量的非相對論性關係,如法泡製得到單原子理想氣體的氣體狀態方程式,結果非常漂亮,這篇論文在1924年9月20日出版。結果雖然漂亮,但是針對這篇論文卻是砲火連連,愛因斯坦推廣玻色統計到一般物質時,會遭到眾人的質疑其實是非常有道理的。因為原先玻色的統計中,擁有相同能量與動量的粒子沒有分別。這件事對於性質不明的光量子也許不是問題,但是對具有質量的原子,那可就不一樣了,因為在古典物理中,任何一顆粒子都是獨一無二的存在,照說這些粒子就算能量與動量相同,我們還是可以根據它們的位置來分辨它們,就算粒子發生碰撞,我們還是能夠分辨哪顆粒子是哪顆,就好比兩台車相撞,總不會說撞完分不出哪台是哪台吧? 即使兩台車是一模一樣的品牌,顏色,光是追蹤兩台車在整個碰撞過程每個瞬間的位置,總還是分辨得出來,不是嗎?
但是愛因斯坦在《單原子理想氣體的量子理論(二)》說明可分辨的粒子寫出來的熵不僅不滿足能斯特定理,也就是溫度趨近於零時熵也要趨近於零,而且兩群相同種類的原子的熵也無法直接相加,但是只要用玻色原先拿來用在光量子的統計用在質點粒子上,這些問題全都迎刃而解。所以情勢變得很尷尬,看來大自然的確採用了玻色主張的統計,怎麼樣才能合理化這個不合理的主張呢?
讓我們回到起點,原先普朗克與玻色研究的都是黑體輻射,普朗克在推導黑體輻射時處理引進了虛擬振子,這些虛擬振子必須彼此不可分辨,才會得到正確結果,事實上,當愛因斯坦在1905年提出光量子理論中,用的還是維恩分布呢,過了將近二十年,玻色終於跨出關鍵的一步,把黑體輻射直接當作光粒子,但是光做為電磁波的特性還是出現在描寫兩偏振方向的因子2上。如果是波的話,兩道波交會後哪道波是從哪道波來的?不可分辨性似乎理所當然,但是當時只有光被認為有波粒二象性,一般的物質,像是電子,明明就是古典力學中的粒子,難道一般的物質也有雙象性?這個想法實在太古怪了,但這正是下封愛因斯坦接到的信的內容!
1924年的夏天,愛因斯坦不但收到玻色從印度來的那封信,幾乎同時,他還收到了一個乍看之下性質完全不同的郵包,原來是他的老朋友,人在巴黎的保羅·朗之萬寄了一份他的博士生寫好的博士論文。這份博士論文的題目是《Recherches sur la théorie des quanta》(量子理論之研究)。這個博士生就是出身貴族世家的路易·維克多·德布羅伊,他在大學時原本讀歷史。後來,認知物理學是他的最愛,開始專心研讀理論物理,跟著保羅·朗之萬研究量子理論。他大約在1923年從與他哥哥合作X光散射實驗的經驗中逐漸產生了物質也有雙象性的概念,而在1924年完稿的博士論文優美地陳述了他的理論,德布羅伊提出了主張,聲稱所有物質,不僅僅是光,都具有波動性質;其波長 (λ) 和動量 (p) 相關聯:p=h/λ。尤其有趣的是他還利用他的物質波理論說明了波爾模型中的角動量量子化條件。但是真正讓愛因斯坦興奮的是,德布羅伊恰恰好給了他將玻色統計用在單原子理想氣體上的理由。愛因斯坦在1924年十一月十六日給朗之萬的回信中,熱切地稱讚了這部論文,不僅興奮地回信給德布羅伊的指導教授朗之萬:「他已經掀起了面紗的一角」之外,還將論文送去柏林科學院,因而使得這理論廣知於物理學界。德布羅伊當然獲得了夢寐以求的博士學位。另一方面,愛因斯坦就在1925年2月9日發表的《單原子理想氣體的量子理論(二)》中特別提到德布羅伊的物質波理論。這篇文章是在1924年十二月完成的。愛因斯坦在哪裡提到德布羅伊的物質波理論呢? 是在論文的第三段,愛因斯坦算了理想氣體原子的粒子數漲落起伏,他發現玻色統計給出
$$\overline{(n_\nu - \overline{n}_\nu)^2} = \overline{\Delta_\nu^2} = n_\nu + \frac{n_\nu^2}{z_\nu}.$$
如果粒子是可分辨的,只會有第一項。愛因斯坦認為粒子相應的波動性能夠解釋第二項。實際上,如果是電子的話,上式應該是
$$\overline{(n_\nu - \overline{n}_\nu)^2} = \overline{\Delta_\nu^2} = n_\nu - \frac{n_\nu^2}{z_\nu}.$$
這個正負號來自於當時愛因斯坦還不知道的另一種量子統計,因為只有這種統計才能滿足一個月前包立提出的不相容原理。或者我們用物質波的概念來說的話,兩顆滿足玻色-愛因斯坦統計的粒子,它們的波函數,在交換粒子標號之後,仍然是原來的波函數。但是這顯然不能滿足包立不相容原理,所以電子滿足另一種統計,兩顆滿足這種未知統計的粒子,它們的波函數,在交換粒子標號之後,會是原來的波函數再乘上一個負號! 這個當時未知的統計後來被費米與狄拉克個別提出,所以被稱為是費米-狄拉克統計。後來科學家更發現所有自旋為整數,如光子自旋為一,滿足的是玻色-愛因斯坦統計:但是自旋為半整數的粒子,像電子這種自旋為1/2 的粒子就必須滿足費米-狄拉克統計。所以我們可以看出物質波與全同粒子,還有自旋這三個觀念之間複雜的三角關係。所以1925年另一個從伏流變成湧泉的概念正是「物質波」,讓我們看看「物質波」這個概念是怎麼出現的,接著再來詳談在1925這一年「物質波」這個概念是如何取得關鍵性的突破。
眾所皆知德布羅伊在1929年就是因為提出「物質波」這個破天荒的概念而榮獲諾貝爾物理獎。德布羅伊的靈感主要來自他的哥哥。路易-塞薩爾-維克多-莫里斯,第六代布羅伊公爵,他畢業於海軍軍官學校,在法國海軍服役九年。服役期間,他對物理學產生了興趣,並開始研究電磁學。莫里斯不顧家人的反對,於 1904 年離開海軍,投身科學事業。他師從朗之萬,並於 1908 年獲得博士學位。莫里斯在 X 射線繞射和光譜學頗有成就,1934年,他當選為法蘭西學院院士。他親自歡迎自己的兄弟也加入法蘭西學院。德布羅伊從哥哥那邊得到許多X光特別是X光繞射的知識,早先陰極射線與X光是波還是粒子都曾引發許多爭論,特別在康普頓著名的實驗之後,X光的粒子性得到證實後,相應地電子是否也擁有波動性開始在他的腦海中萌生了。
但是德布羅伊的絕妙點子之所以能衍生出波動力學,也就是第二個版本的量子力學還是要歸功於薛丁格。他的全名是埃爾溫·魯道夫·約瑟夫·亞歷山大·薛丁格(Erwin Rudolf Josef Alexander Schrödinger;1887—1961)他在1906年至1910年在維也納大學學習物理與數學,並在1910年取得博士學位,薛丁格在1914年至1918年參加了第一次世界大戰。此後在耶拿大學、司徒加特大學、布雷斯勞大學,最後在1921年他落腳在蘇黎世大學教書。
綜觀薛丁格早年的工作,其實涵蓋的範圍還蠻廣的。他年輕曾從事大氣電學和大氣放射性領域的實驗,這些研究通常是與他的指導教授弗朗茨·埃克斯納(Franz Exner)一起做的。他也曾研究過振動理論、布朗運動理論和數理統計。 1912年,應《電磁學手冊Handbook of Electricity and Magnetism》編輯之邀撰寫過一篇題為《介電性》的文章。同年,他對放射性物質的可能高度分佈進行了理論估計,用來解釋觀測到的大氣放射性。 1913年8月,他在齊哈姆進行了幾次實驗,證實了他和發現宇宙射線的奧地利科學家,維克多·赫斯的理論估計。由於這項工作,他於1920年獲得了奧地利科學院的海廷格獎。 這位年輕的研究員在1914年進行的其他實驗研究包括檢驗氣泡中毛細管壓力的公式,以及伽馬射線撞擊金屬表面產生的軟β輻射的性質。這是他與好友弗里茲·科爾勞施(Fritz Kohlrausch)合作完成的。 1919年,他完成了最後一個物理實驗,隨後就不做實驗,改而專注於理論研究。透過研讀愛因斯坦、普朗克、波爾、索末菲等人著作,薛丁格逐漸對當時的量子理論產生興趣。 1921年1月,薛丁格完成了他關於這個主題的第一篇文章,探討了電子相互作用的波爾-索末菲量子化框架對鹼金屬光譜某些特徵的影響。他特別感興趣的是將相對論的考慮引入量子理論。 1922年秋,他運用好朋友赫爾曼·外爾(Hermann Weyl)發展的方法,從幾何角度分析了原子中的電子軌道。雖然不是量子物理的門外漢,但是顯然他與哥本哈根的波爾,哥廷根的波恩,慕尼黑的索末菲並沒有特別密切的往來,所以他是如何能夠另闢蹊徑,開創出波動力學的呢?箇中緣故眾說紛紜,筆者只能把各家說法收集在一起。其中一說是第四次索爾維會議在1924年四月二十四日到二十九日在布魯賽爾舉行時,朗之萬與德拜與薛丁格都有參加,有此一說,就在會場上他們就聽說了物質波。那一次的會議沒有邀請任何德國學者,因為當時歐洲對於戰時德國眾多學者簽署九三宣言力挺德皇與德軍,依然無法忘懷,所以除了當年拒絕簽署九三宣言的愛因斯坦以外都沒有接到邀請。但是愛因斯坦當然也婉拒參加,免得成為德國同行的眼中釘。德拜是在瑞士蘇黎世的瑞士聯邦理工學院(ETH)任教的荷蘭人,薛丁格是在蘇黎世大學任教的奧地利人,所以有人推測薛丁格可能在會場上就從朗之萬那裡聽說了物質波,因為索爾維會議向來就是以物理學家在會場外杯觥交錯,酒酣耳熱之餘迸出物理的火花而聞名。也由於愛因斯坦沒有參加會議,所以朗之萬才將德布羅伊的論文寄給他。但是看來一開始薛丁格似乎沒把物質波當一回事,什麼時候他才認真思考物質波的呢?
由於薛丁格自己從來不提,也沒留下隻字片語。所以他何時開啟物質波的研究成了物理史上的一大羅生門。德拜在1962年時回憶道他當年親手將德布羅伊在1925年發表的論文,而非博士論文,拿給薛丁格。德拜在1964年加碼提到當年是他向薛丁格提議在ETH與蘇黎世大學聯合的定期書報討論研討會上,給個與德布羅伊波相關的報告。當時在ETH唸書的 布拉赫也證實了在1925年的年底,薛丁格的確給了一個很讚的報告,布拉赫還記得德拜當時要求薛丁格給這個演講時事怎麼說的:「薛丁格,反正你最近也沒在做什麼重要的工作﹐要不要順便給我們講一下德·布羅伊那個蠻有趣的點子?」當薛丁格講完之後,德拜還批評道:既然是波,就要有波方程呀。然而德拜是不是認真的呢? 根據德拜的師弟,同樣也是索末菲學生的蘭德,他在1962的訪談是這麼說,
…1925年我在蘇黎世。當時德拜是蘇黎世的教授,薛丁格也是。我很了解德拜,也跟他聊過天。他說:「蘭德,你覺得這個瘋狂的想法怎麼樣——薛丁格想用波來解決量子問題。這難道不瘋狂嗎?」…
所以看來薛丁格周遭的人對物質波能不能解決量子物理的難題到底有多大的信心,還真是天曉得。嗯,那到底薛丁格在1925年在忙些什麼呢? 前一年波爾、克拉默斯(Hans Kramers)和斯拉特(John C. Slater)在一月剛提出BKS理論,該理論表明在單個原子過程中(例如,在輻射發射過程中)可能違反這些定律。有興趣的讀者請參閱「關於黑爾戈蘭島傳說」一文。
薛丁格欣賞老師埃克斯納(Exner)關於守恆定律統計性質的觀點,因此熱情地接受BKS理論。儘管1925年四月博特-蓋格的實驗證實了康普頓散射中能量與動量都是嚴格守恆,但能量作為統計概念的想法卻終生吸引著薛丁格,他在一些報告和出版物中對此進行了討論。 薛丁格在這一年五月接受慕尼黑的維恩的邀請,撰寫色彩理論與視覺相關生理學機制的文章,可惜最後沒有完成。但是真正佔了他最多時間的,應該是關於單原子理想氣體的熵。薛丁格在1925年正忙著研究單原子理想氣體的熵,他與愛因斯坦,普朗克與蘭德頻繁地通信,通信的內容都是與量子系統的統計性質有關。他在十一月三日寫給愛因斯坦的信以及十一月十六日寫給蘭德的信都提到德布羅伊波,信裡也同時針對蘭德企圖在粒子的統計行為中混入波的性質提出反駁,但是他在寫給蘭德的信中,卻也喊出「想要回到光的波動理論,甚至用德布羅伊的波動理論來處理波爾模型中的電子軌道。」的心聲。但是從這些信中都沒有透露他用波動理論研究氫原子能階的蛛絲馬跡。意外的是,根據狄拉克在1961年悼念薛丁格的文章中的回憶,薛丁格曾告訴狄拉克,在他發表波動力學的幾個月前,他曾經利用滿足特殊相對論不變性的波方程式(後來被稱為克萊因-戈登方程式) 試圖得到電子的能階,但是卻得到與先前索末菲精細結構公式不同的結果,後來的學者從薛丁格留下的筆記手稿中發現,雖然沒有紀錄日期,但是確實發現了薛丁格的相對論性波方程式計算氫原子能階的概要,狄拉克還回憶道,當時薛丁格非常地失望,因為當時大家公認索末菲的結果與實驗的吻合非常地好,所以他把結果放進抽屜,完全不打算發表,但是在1926一月, 薛丁格在 Annalen der Physik 就發表了第一篇波動力學的論文"Quantisierung als Eigenwertproblem“,接著如排山倒海之勢,一口氣發表了四篇波動力學的論文,所以顯然,薛丁格是在1925年的年底把放進抽屜的計算重新拿出來,在幾個禮拜內,把滿足相對論不變性的波方程改成非相對論性的波方程,也就是我們今天熟悉的薛丁格方程式。有趣的是,克萊因-戈登方程式之所以沒有得到正確的結果是因為沒有把先前提到的包立所發現的電子自旋考慮進去,要等到兩年後,狄拉克才寫出滿足相對論不變性的自旋二分之一的波動方程式,得到正確的答案。
所以我們看到,就在1925年間,研究量子物理的各路思潮如百川納海一般,逐漸匯流成一片汪洋大海,真可謂是量子物理的奇蹟之年。到了1926年,海森堡在採用了包立不相容原則與薛丁格方程式,解釋了量子物理中一直無法解釋的氦原子光譜,而多位科學家也在1926年發覺到波動力學其實與哥廷根學派的矩陣力學其實享有相同的數學結構。可以說一路從1925年到1928年狄拉克寫下著名的狄拉克方程式為止,量子物理從一團謎霧迅速地成為一片繁花盛開的樂園,百年之後,眾多建立在量子力學基礎上的新科技正在快速地改變著我們的世界,2025年這個「國際量子科學技術年」能不能像1925年那樣後世的肯定,就看我們這個世代的努力囉。

